데이터의 이산 푸리에 변환
• dft(A), idft(Z) - 복소수 값 벡터나 행렬의 정방향 또는 역방향 푸리에 변환을 구합니다.
dft의 입력이 길이 r인 벡터 V인 경우
◦ dft(V)의 출력은 길이 r인 벡터 Z입니다.
◦ idft(Z)의 출력은 길이 r인 벡터입니다.
dft의 입력이 r행 및 c열인 행렬 M인 경우
◦ dft(M)의 출력은 r행 및 c열인 행렬 P입니다.
◦ idft(P)의 출력은 r행 및 c열인 행렬입니다.
• dftr(B), idftr(Z) - 실수 값 벡터나 행렬의 정방향 또는 역방향 푸리에 변환을 구합니다.
dftr의 입력이 길이 r인 벡터 V인 경우
◦ dftr(V)의 출력은 길이 Z인 벡터 L이며, 여기서 L=floor(r/2)+1입니다. Z의 요소는 dft(V)의 출력의 첫 번째 L 요소와 동일합니다.
◦ idftr(Z)의 출력은 길이 r=2(L-1)인 벡터입니다.
dftr의 입력이 r행 및 c열인 행렬 M인 경우
◦ dftr(M)의 출력은 P행 및 r열인 행렬 L입니다(여기서, L=floor(c/2)+1). P의 요소는 dft(M)의 출력의 첫 번째 L열과 동일합니다.
◦ idftr(P)의 출력은 r행 및 c=2(L-1)열인 행렬입니다.
인수
• A는 임의 크기의 복소수 값 벡터 또는 행렬입니다.
• B는 실수치 벡터 또는 행렬입니다. 모든 허수 부분은 무시됩니다. B가 벡터인 경우 행 수는 2의 배수여야 합니다. B가 행렬인 경우 열 수는 2의 배수여야 합니다
• A와 B 모두의 경우 데이터의 단위는 호환되어야 합니다.
벡터 푸리에 변환
• A가 크기 m인 벡터인 경우 벡터 A의 1차원(1D) 순방향 변환에서 u번째 요소는 다음과 같이 Zu로 지정됩니다.
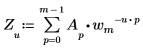
여기서
◦ m은 행 수이고 u는 다음과 같이 정의됩니다. 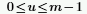
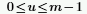
◦ i는 허수 단위이고 wm은 다음과 같이 정의됩니다.
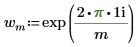
위 정의에서 Z를 계산하는 것은 벡터 A에 dft 함수를 적용하는 것과 동일합니다.
• Z가 크기 m인 벡터인 경우 벡터 Z의 1차원(1D) 역방향 변환에서 u번째 요소는 다음과 같이 Au로 지정됩니다.
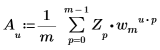
여기서
◦ m, u 및 wm은 위에 정의되어 있습니다.
위 정의에서 A를 계산하는 것은 벡터 Z에 idft 함수를 적용하는 것과 동일합니다.
행렬 푸리에 변환
• A가 크기 mxn인 행렬인 경우 행렬 A의 2차원(2D) 순방향 변환에서 (u,v)번째 요소는 다음과 같이 Zu,v로 지정됩니다.
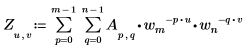
여기서
◦ m, u 및 wm은 위에 정의되어 있습니다.
◦ n은 열 수이고 v는 다음과 같이 정의됩니다. 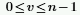
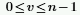
◦ i는 허수 단위이고 wn은 다음과 같이 정의됩니다.
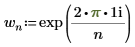
위 정의에서 Z를 계산하는 것은 행렬 A에 dft 함수를 적용하는 것과 동일합니다.
• Z가 크기 mxn인 행렬인 경우 행렬 A의 2차원(2D) 역방향 변환에서 (u,v)번째 요소는 다음과 같이 Au,v로 지정됩니다.
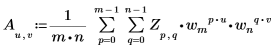
여기서
◦ m, n, u, v, wm 및 wn은 위에 정의되어 있습니다.
위 정의에서 A를 계산하는 것은 행렬 Z에 idft 함수를 적용하는 것과 동일합니다.
추가 정보
• 푸리에 함수는 벡터 행 및 행렬 열의 수가 2의 거듭곱일 때 더욱 빠르게 실행됩니다.
• 새로운 dft/idft 함수는 더 이상 사용되지 않는 cfft/icfft 및 CFFT/ICFFT 함수의 기능을 대체하며, 대규모 데이터 집합이거나 크기가 2의 배수가 아닌 경우 특히 함수의 성능이 상당히 높습니다.
• 새로운 dftr/idftr 함수는 더 이상 사용되지 않는 fft/ifft 및 FFT/IFFT 함수의 기능을 대체합니다.
함수 dftr은 길이가 짝수인 실수 벡터와 열 수가 짝수인 행렬에서 작동합니다.
• 함수 fft/FFT는 길이가 2의 거듭곱인 실수 벡터에서만 작동합니다.
• 함수 ifft/IFFT는 입력 벡터 길이의 절반에 1을 더한 값 또는 2k-1+1(여기서 k는 1보다 큰 정수)을 길이로 갖습니다. 나머지 절반은 순서가 뒤바뀐 첫 번째 부분의 공액 부분으로 수동으로 재구성해야 합니다. 함수 dft/idft는 전체 결과를 구합니다.
• 함수 dft/idft는 배율 인수와 지수 기호 모두에서 더 이상 사용되지 않는 fft/ifft, FFT/IFFT 및 cfft/icfft, CFFT/ICFFT와 다릅니다.
◦ 순방향 변환의 경우 다음과 같은 차이점이 있습니다.
dft/dftr | fft/cfft | FFT/CFFT | |
|---|---|---|---|
배율 인수 | 1 | 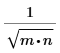 | 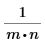 |
지수 기호 | 음수 | 양수 | 음수 |
◦ 역방향 변환의 경우 다음과 같은 차이점이 있습니다.
idft/idftr | ifft/icfft | IFFT/ICFFT | |
|---|---|---|---|
배율 인수 | 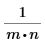 | 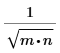 | 1 |
지수 기호 | 양수 | 음수 | 양수 |
벡터에서만 작동하는 함수의 경우(1D 경우) 배율 인수를 계산할 때 n=1이라고 가정합니다.