状態空間 ODE ソルバー
• statespace(init, t1, t2, intvls, A, [B, u]) - 次の形式の連立 1 階線形常微分方程式の解を返します。
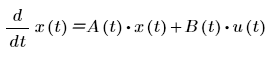
ここで
◦ x(t)
は未知の状態ベクトルです。
◦ A(t)
はベクトル x(t) の関数間のカップリングを表す状態行列です。
◦ B(t)
は入力ベクトル u(t) の項の間のカップリングを表す入力行列です。
◦ u(t) は入力ベクトルです。
この関数は、(intvls+1)×(n+1) の解行列を返します (ここで n は未知の状態の個数)。行列の最初の列には、解が評価された点の t の値が含まれています。これらの値は t1 から t2 の間を (intvls+1) 個に等間隔で区切った点の数値です。以降の列には、最初の列の t の値に対応する解 x0, x1, ..., xn-1 の値が含まれています。
引数
• init は初期条件の列ベクトルです (ベクトルの長さは未知の状態の数と等しい)。
• t1 は積分区間の始点を指定する実数です。
• t2 は積分区間の終点を指定する実数です。
• intvls は、解の関数を補間するときに使用する離散化間隔の数を示す整数です。間隔の数に 1 を加えた数が解の点の数になります。
• A は A(t) という形式の n × n の行列関数です (ここで n は未知の状態の個数)。A(t) のエントリは独立変数 t の関数です。
• B (オプション) は B(t) という形式の n × k 行列またはベクトル関数です。このエントリは t の関数です。
• u (オプション) は u(t) という形式の k × 1 ベクトルまたはスカラー関数です。このエントリは t の関数です。
引数 Bを指定した場合、u を必ず指定する必要があります。
• x (オプション) は x(t) という形式の k × 1 ベクトルまたはスカラー関数です。このエントリは t の関数です。
引数 Aを指定した場合、x を必ず指定する必要があります。
追加情報
この表記では独立変数 t の未知数のベクトルが x(t) で表されています。これはほかの ODE ソルバのヘルプページで使用されている表記とは異なります。その他のヘルプページでは、文字 x が独立変数を表し、y(x) が未知数のベクトルを表しています。