Ecuaciones diferenciales parciales en bloques de resolución
pdesolve(u, x, xrange, t, trange, [xpts], [tpts]): devuelve una función o un vector de funciones u(x,t) que resuelve una ecuación diferencial parcial (PDE) no lineal unidimensional o un sistema de PDE con restricciones de igualdad independientes n para una ecuación diferencial de orden n. Los valores se interpolan a partir de una matriz de puntos de solución calculados mediante el método numérico de líneas.
Debe utilizar pdesolve en un bloque de resolución.
Argumentos
• u es un nombre de función escalar o un vector de nombre de función (sin incluir nombres de variables), tal como aparecen dentro del bloque de resolución. Por ejemplo, si resuelve las funciones f(x,t) y g(x,t), u sería:
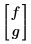
Para ajustar la notación diferencial parcial de subíndice, no puede utilizar subíndices literales al asignar nombres a funciones.
• x es el nombre de la variable espacial.
• xrange es un vector de columna de dos elementos que contiene los valores de límite reales de x.
• t es el nombre de la variable tiempo.
• trange es un vector de columna de dos elementos que contiene los valores de límite reales de t.
• xpts (opcional) es el número entero de puntos de discretización espacial.
• tpts (opcional) es el número entero de puntos de discretización temporal.
Se aplican las reglas generales de definición de un bloque de resolución. Dentro del cuerpo del bloque:
Funciones desconocidas
Las funciones se deben definir según sus variables. Por ejemplo, utilice u(x,t), no u. Para indicar una derivada parcial dentro del bloque de resolución, utilice una de las siguientes opciones:
• Notación de subíndice. Por ejemplo, uxx(x,t) es la segunda derivada parcial de u con respecto a x.
La notación de subíndice solo puede utilizarse en pdesolve en bloques de resolución y no en otras regiones de la hoja de trabajo. |
Ecuaciones PDE
Las ecuaciones deben definirse con iguales booleanos. Las derivadas segundas parciales no están permitidas en el lado izquierdo de las ecuaciones, por lo que debe convertir la ecuación en un sistema de ecuaciones solo en las primeras derivadas.
Condiciones de límite
Debe haber una condición inicial u(x,0) y condiciones de límite n, donde n es el orden de la PDE para cada función desconocida. Mathcad comprueba el tipo correcto y el número de restricciones, y señala los errores con un mensaje de error.
• Las condiciones de límite pueden ser de tipo Dirichlet (u(0,t) = f(t)), Neumann (ux(0,t)=g(t)) o una combinación de ambas.
• Las condiciones de límite pueden especificarse en cualquier punto final del rango de integración espacial. Los puntos finales utilizados en las condiciones de límite deben coincidir con los puntos finales especificados en el comando ode/pdesolve.
• Aunque Mathcad puede resolver una función pdesolve con una condición de límite implícita, en algunos casos, la función pdesolve no puede resolverse debido a las limitaciones de los algoritmos de aproximación. Por tanto, se recomienda usar condiciones de límite explícitas, cuando sea posible.
Restricciones
Se permiten restricciones algebraicas de la forma u(x,t)+v(x,t)+w(x,t)=0. Esto añade una función w desconocida adicional al sistema, que debe especificarse como una de las funciones de salida en la llamada ode/pdesolve. No están permitidas las restricciones de desigualdad.
• Asigne la salida de la función pdesolve a un nombre de función o a un vector de nombres de función.
• Para cambiar el método de aproximación utilizado para las derivadas parciales, pulse con el botón derecho del ratón en la función pdesolve y elija otro método. Esto puede afectar al tiempo de cálculo.
• El método numérico de líneas solo es adecuado para resolver PDE hiperbólicas y parabólicas, así como ecuaciones algebraicas parciales. Utilice numol para resolver una ecuación en un bucle de programa. Para resolver una PDE elíptica, como la ecuación de Poisson, utilice Relax o Multigrid.
Errores y solución con pdesolve
• Error: esta función requiere al menos 5 argumentos, pero se aplica a 4.
Ejemplo:
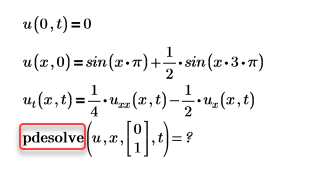
Solución: añada el argumento que falte; en este caso, es trange.
• Error: Esta función acepta como máximo 7 argumentos pero se aplica a 8.
Ejemplo:
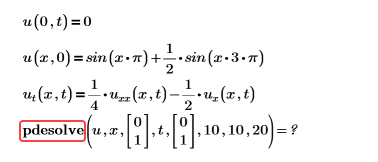
Solución: quite los argumentos innecesarios. Obtenga más información sobre los argumentos.
• Error: vector de contornos mal formado para la variable tiempo.
Ejemplo:
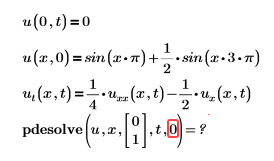
Solución: trange no está definido correctamente. Obtenga más información en la sección Argumentos.
• Error: vector de contornos mal formado para la variable espacial.
Ejemplo:
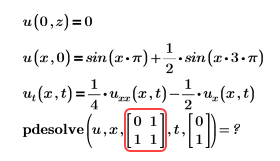
Solución: xrange no está definido correctamente. Obtenga más información en la sección Argumentos.
• Error: el nombre de la función desconocida no se ha especificado correctamente.
Ejemplo:
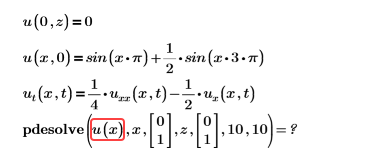
Solución: la función debe aparecer sin ningún argumento.
• Error: Este valor debe ser un entero mayor que 4.
Ejemplo:
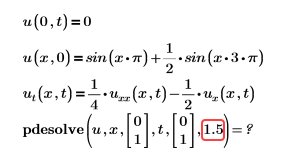
O
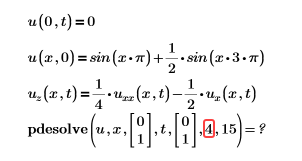
Solución: el número de puntos de discretización debe ser un entero mayor que 4.