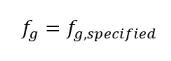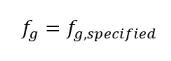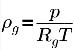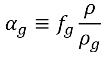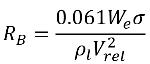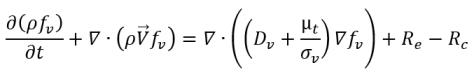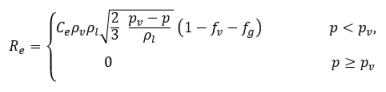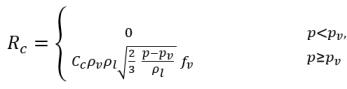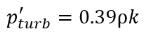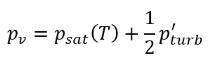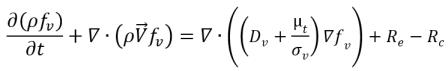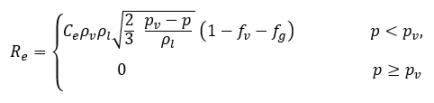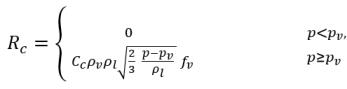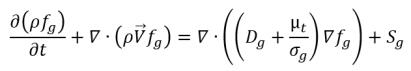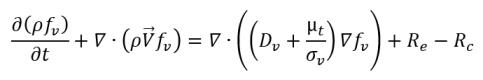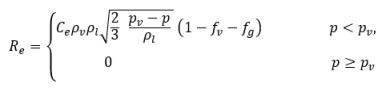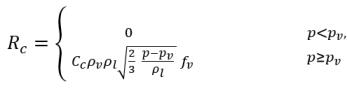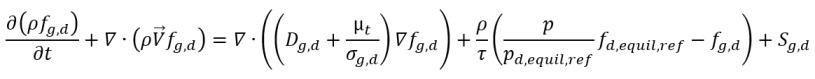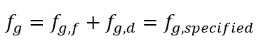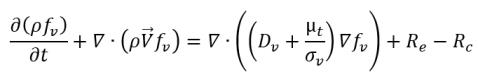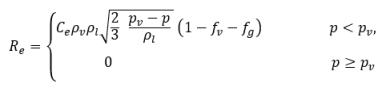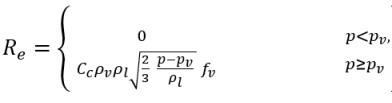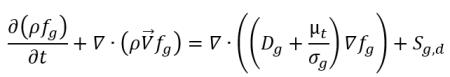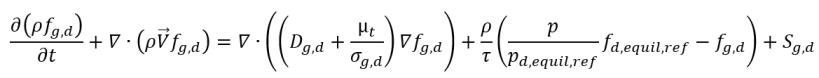Cavitation Models
In Creo Flow Analysis, as in the original Singhal et al model, the working fluid in cavitating flows is always assumed to be a mixture of liquid, vapor and some noncondensable gases. By default, the cavitation models account for both liquid-vapor phase change and the effect of noncondensable gases. Based on the modeling approach for noncondensable gas effect, five different models are provided in the following table for the prediction of the aeration and cavitation in a liquid system. These models are described in detail in this section.
|
Models for NCG
|
Description
|
|
Constant Gas Mass Fraction
|
Mass fraction of the (noncondensable gas) NCG is constant and considered to be out of solution with tiny compressible bubbles
|
|
Variable Gas Mass Fraction
|
Similar to the Constant Gas Mass Fraction model, but the mass fraction of NCG can vary, such as inlets can introduce different mass fractions
|
|
Equilibrium Dissolve Gas Model
|
Mass fraction of the NCG dissolved in the liquid is equal to the equilibrium value
|
|
Dissolved Gas Model
|
Mass fraction of the NCG dissolved in the liquid depends on the rate of absorption or desorption and the equilibrium value
|
|
Full Gas Model
|
Combines the Dissolved Gas Model and Variable Gas Mass Fraction
|
Constant Gas Mass Fraction Model
The constant gas mass fraction model is the basic or default cavitation model in Creo Flow Analysis. It is based on the work by Singhal et al. This model assumes that in the working fluid, the ever-present noncondensable gas (NCG) in the liquid is a nondissolvable gas or free gas bubbles that follow the ideal gas law. Though all the predescribed noncondensable gas can freely expand with the decrease of the pressure in cavitating zones, the mass fraction of noncondensable gases is predescribed and remains the same in a cavitating flow:
equation 2.217
where f g,specified is a user-specified value.
The density of the noncondensable gas follows the ideal gas law:
equation 2.218
where T is the fluid temperature, which is predescribed (isothermal flow) or obtained by solving the mixture energy conservation
equation 2.168 when heat transfer is considered. From
equation 2.173, the volume fraction of the noncondensable is as follows:
equation 2.219
Though the mass fraction of NCG is fixed and usually has a small value of 1.5e-05 or 15 ppm in natural water, its volume fraction αg varies and can be larger in value. In cavities or low pressure zones the noncondensable gas competes with the vapor to fill the void in space depending on the gas and vapor densities.
For the liquid-vapor mass transfer,
equation 2.194 and
equation 2.195 serve as the foundation to construct the cavitation source and sink term in the vapor mass fraction
equation 2.169. Specifically, the bubble radius, R
B needs to be estimated using the known flow quantities during both bubble growth and collapse.
Singhal et al argued that if the typical bubble size R
B is the same as the limiting (maximum possible) bubble size, then R
B is determined by the balance between the aerodynamic drag and surface tension forces. A correlation used in the nuclear industry is:
equation 2.220
where Vrel is the magnitude of the liquid-vapor relative velocity. In the bubbly flow regime under which cavitation occurs, Vrel is generally small at around 5-10% of liquid velocity. By using various limiting arguments such as RB →0 as αv →0 and the fact that the phase change rates per unit volume should be proportional to the volume fractions (or mass fractions) of the donor phase, the following expressions for vapor generation / condensation rates are obtained to complete the cavitation model as:
equation 2.221
equation 2.222
equation 2.223
where C
e and C
c are the evaporate and condensate coefficients, which can be user-specified constant values that are set by default to 1.0, or functions of known flow quantities. In
equation 2.222 and
equation 2.223, a new threshold pressure ρ
v is introduced to replace the saturation vapor pressure ρ
sat in
equation 2.194 and
equation 2.195. According to
Singhal et al, to account for the effect of turbulence on cavitating flows, observed by experimental investigations, a local value of the turbulent pressure fluctuations given by
Hinze:
equation 2.224
is added to the saturation vapor pressure to raise the phase-change threshold pressure value to:
equation 2.225
For laminar flows, pv=psat(T)
When heat transfer is considered and all the phase densities including liquid, vapor, and noncondensable gases are subjected to changes with temperature, the saturation vapor pressure psat is also a function of temperature. Consequently, the direct thermal effect on cavitation can be considered in this cavitation model.
Variable Gas Mass Fraction Model
The variable gas mass fraction model assumes that the noncondensable gas always remains as a free gas which cannot be dissolved into the liquid, but the mass fraction is no longer a predescribed constant as in the constant gas mass fraction model. Instead, the distribution of the local mass fraction is governed by a transport equation. While the liquid-vapor mass transfer is modeled by the same cavitation model referenced in
equation 2.221,
equation 2.222, and
equation 2.223. For clarity, the complete set of the modeling equations is given below:
• Liquid-Vapor Phase Change
equation 2.226
where
equation 2.227
equation 2.228
• Noncondensable Gas Transport Equation
Following
equation 2.199, the transport equation for the noncondensable gas (f
g) is:
equation 2.229
where Sg is the external or user-defined source for the noncondensable gas.
Equilibrium Dissolve Gas Model
In cavitating flows, the noncondensable gases in the fluid are dissolved into or released from a liquid to achieve a dynamic equilibrium of the mass concentrations between the liquid and gas phases. The Equilibrium Dissolve Gas Model assumes that the mass fraction of the total noncondensable gas remains as a constant. However, a part of it is dissolved into the liquid to instantly satisfy the local equilibrium condition. Mathematically, in addition to the same mass fraction equation for vapor and vapor mass transfer models, it solves an additional transport equation for the mass fraction of the dissolved gas fgd, which is assumed to be always in equilibrium state. The modeling equations are as follows:
• Liquid-Vapor Phase Change
equation 2.230
where
equation 2.231
equation 2.232
• Gas Absorption/Dissolution or Release
equation 2.233
where
Sg,d | user-defined law of gas dissolution or release |
fd,equil,ref | equilibrium mass fraction of the dissolved gas at the reference pressure pd,equil,ref |
fd,equil,ref and pd,equil,ref | user-specified values |
In this equilibrium model, the time scale Γ approaches zero so that the mass transfer is near instant. Note that in
equation 2.231, the free gas has the mass fraction f
g,f, instead of f
g. The mass fraction of the free gas is obtained from the condition:
equation 2.234
where fg,specified is a user-specified value.
Dissolved Gas Model
This model relaxes the condition that the dissolved gas in the liquid is always at the equilibrium state. Instead of being determined by the equilibrium condition with instant mass transfer, the mass fraction of the dissolved gas (f
g,d) depends on the transport of the component and the dissolution or release rate (finite rate). Therefore, the dissolved gas model shares the same modeling formulations as the equilibrium dissolve gas model,
equation 2.230-
equation 2.234. However, the finite rates of mass transfer for gas dissolution and release are characterized by the different time scales (Γ). For the gas absorption or dissolution into the liquid, Γ is given by a specified absorption time (dissolved gas dissolve time by default is 10 s). For the release of dissolved gas from the liquid, the rate of mass transfer is dictated by a specified gas release time (dissolved gas release time by default Γ is 10 s).
Full Gas Model
The full gas model is a combination of the dissolved gas model and variable gas model. The mass fraction of the noncondensable gas is subjected to change with time and space, while the gas dissolution or absorption and release can also occur for the noncondensable gases. The complete set of modeling equations is given below:
• Liquid-Vapor Phase Change
equation 2.235
where
equation 2.236
equation 2.237
• Transport of Noncondensable Gas
equation 2.238
• Gas Dissolution or Release
equation 2.239