Consideraciones especiales del modelo de volumen de fluido (VOF)
Modelo VOF frente al modelo de mezcla
En el método de modelado multifase euleriano homogéneo, los modelos eulerianos de volumen de fluido (VOF) y de mezcla resuelven el mismo conjunto de ecuaciones gobernantes de la mezcla (promedio). Sin embargo, se basan en diferentes mecanismos físicos y se aplican a distintos regímenes de flujo multifase:
• Modelo de mezcla: está diseñado para dos o más fases (fluido o con partículas), que se tratan como interpenetrantes y continuas. Proporciona una solución para la ecuación del momento de la mezcla y las ecuaciones de energía y no se hace seguimiento de la interfaz fase-a-fase o no se observa ninguna interfaz clara. Entre las aplicaciones del modelo de mezcla se incluyen flujos cargados de partículas con carga baja, flujos con burbujas y gotas, sedimentación y separadores ciclónicos. El modelo de mezcla también se puede utilizar con velocidades relativas prescritas para las fases dispersas a fin de modelar flujos multifase no homogéneos.
• Modelo VOF: suele ser una técnica de seguimiento transitorio de superficie diseñada para dos o más fluidos inmiscibles donde la posición de la interfaz fase-a-fase es de interés. En el modelo de VOF, un único conjunto de ecuaciones de momento y energía de la mezcla se comparte entre todas las fases y se resuelve implícitamente. Las fracciones volumétricas de fase se obtienen mediante precisos algoritmos de tiempo explícitos o implícitos con esquemas de advección de orden superior para resolver interfaces significativas entre un par de fases. Entre las aplicaciones típicas del modelo de VOF se incluyen flujos estratificados, flujos de superficie libre, relleno, chapoteo, movimiento de burbujas grandes en un líquido, movimiento de líquido después de la rotura de una presa, predicción de la rotura de un surtidor (tensión de superficie) y seguimiento de cualquier interfaz líquido-gas.
La formulación de VOF se basa en el hecho de que dos o más fluidos (o fases) no se interpenetran. Por lo tanto, en cualquier celda determinada del volumen de control, las fracciones volumétricas de fase local pueden determinar si solo contiene una de las fases o una mezcla de fases. Por ejemplo, para la fase qth, si la fracción volumétrica en una celda es αq, solo son posibles las tres condiciones siguientes:
◦ αq = 0: la celda está vacía de la fase qth
◦ αq = 1: la celda está llena de la fase qth
◦ 0< αq < 1: la celda contiene la interfaz entre la fase qth y una o más fases.
Por lo tanto, se puede realizar el seguimiento de las interfaces entre las fases de la solución de una ecuación de transporte para la fracción volumétrica de una o varias de las fases.
Efecto de la tensión de superficie
La tensión de superficie es la tendencia elástica de una superficie de fluido que le hace adquirir el área de superficie menor posible. Consideremos una burbuja de aire en un líquido. Dentro de la burbuja, la fuerza neta de una molécula debido a sus vecinas es cero. En las interfaces líquido-aire, la tensión de superficie es el resultado de la atracción mayor de las moléculas de líquido entre sí debido a la cohesión en lugar de las moléculas en el aire debido a la adhesión. El efecto neto es una fuerza radial hacia adentro en la superficie, que hace que la burbuja se contraiga. La presión dentro de la burbuja aumenta para compensar la fuerza de atracción intermolecular.
• Modelo de fuerza de superficie continua
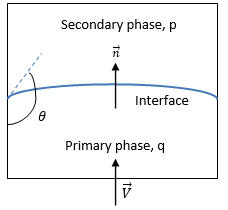
En Creo Flow Analysis, en el modelo de VOF se pueden incluir los efectos de la tensión de superficie a lo largo de la interfaz entre cada par de fases. El modelo de tensión de superficie adoptado se basa en el modelo de fuerza de superficie continua (CFS) de Brackbill et al. En este método, se considera el efecto de la tensión de superficie como una fuerza volumétrica adicional concentrada en la interfaz, en lugar de una fuerza de superficie. Para la interfaz de superficie libre que se muestra en la figura 2.26, el fluido principal es la fase q (fase líquida) y el fluido secundario es la fase p (normalmente una fase gaseosa). Según el modelo de fuerza de superficie continua, la curvatura de la superficie se calcula a partir de gradientes locales en la normal de la superficie de la interfaz. Deje que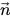 
sea el vector normal a la superficie, definido como el gradiente de la fracción volumétrica del fluido principal, αq:
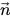sea el vector normal a la superficie, definido como el gradiente de la fracción volumétrica del fluido principal, αq: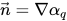
La curvatura de la interfaz k, se define en términos de la divergencia del vector normal unitario:
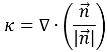
ecuación 2.93
donde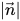 
es la magnitud del vector .
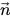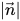es la magnitud del vector 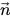.La fuerza de la tensión de superficie en la superficie se expresa como una fuerza volumétrica mediante el teorema de divergencia, que es un término de origen adicional añadido a la ecuación del momento de la mezcla:
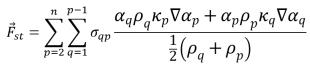
ecuación 2.94
donde σqp es el coeficiente de tensión de superficie entre el fluido q y el fluido p. Tiene la unidad N/m. La ecuación 2.94 permite una superposición suave de fuerzas cerca de las celdas donde están presentes más de dos fases. Si solo están presentes dos fases en una celda, existen las siguientes relaciones:
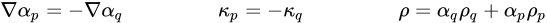
ecuación 2.95
donde ρ es la densidad de la mezcla. Luego la ecuación 2.94 se reduce a
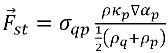
ecuación 2.96
• Inclusión de la fuerza de tensión de superficie
La importancia de los efectos de la tensión de superficie se determina por dos parámetros sin cotas el número Re de Reynolds y el número de capilaridad Ca o el número de Reynolds y el número de Weber We:
Si Re<<1, el parámetro de interés es el número de capilaridad:
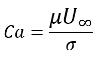
ecuación 2.97
donde U∞ es la velocidad de flujo libre. Se hace caso omiso de los efectos de la tensión de superficie si Ca>>1, ya que la fuerza de la tensión de superficie es demasiado pequeña.
Si Re>>1, el parámetro de interés es el número de Weber:
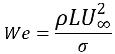
ecuación 2.98
donde L es la longitud característica. También se pueden desestimar los efectos de la tensión de superficie si We>>1, cuando la fuerza de inercia es mucho mayor que la fuerza de la tensión de superficie.
Adhesión de pared (ángulo de contacto)
El modelo de volumen de fluido (VOF) dispone de una opción para especificar un ángulo de adhesión de la pared en combinación con el modelo de tensión de superficie. Según Brackbill et al., en lugar de la aplicación de esta condición de límite en la pared directamente, se utiliza el ángulo de contacto entre el fluido y la pared en la interfaz para ajustar la normal de la superficie en las celdas cercanas a la pared. Esta condición de límite dinámico resulta en el ajuste de la curvatura de la superficie cerca de la pared.
Si θ es el ángulo de contacto de la interfaz de superficie libre en la pared, tal como se muestra en la figura 2.26, el vector normal unitario cerca de la celda de la pared se calcula como:
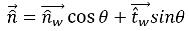
ecuación 2.99
donde,
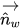 | vector unitario normal a la pared |
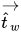 | vector unitario tangencial a la pared |
Luego se utiliza la unidad de velocidad normal calculada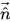 
para determinar la curvatura local de la superficie, la ecuación 2.93 y posteriormente la fuerza de la tensión de superficie, la ecuación 2.94 o la ecuación 2.95.
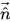para determinar la curvatura local de la superficie, la ecuación 2.93 y posteriormente la fuerza de la tensión de superficie, la ecuación 2.94 o la ecuación 2.95.