Física
En esta sección se describen la teoría y el modelado en el módulo a través de los siguientes temas:
Ecuación de transporte escalar
En el módulo Especies (Species), Creo Flow Analysis resuelve la ecuación de transporte para un escalar arbitrario, definido por el usuario. En el caso de un escalar arbitrario,  , la ecuación de transporte general tiene el siguiente formato:
, la ecuación de transporte general tiene el siguiente formato:
 , la ecuación de transporte general tiene el siguiente formato:
, la ecuación de transporte general tiene el siguiente formato: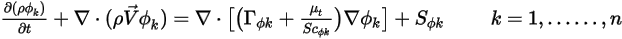
donde 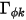 ,
, 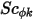 y
y  son el coeficiente de difusión especificado por el usuario, el número de Schmidt turbulento y el término de origen para el escalar
son el coeficiente de difusión especificado por el usuario, el número de Schmidt turbulento y el término de origen para el escalar 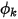 , respectivamente. Aquí
, respectivamente. Aquí 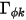 se supone que es isótropo. Puede ser un valor especificado directamente o una función definida por el usuario.
se supone que es isótropo. Puede ser un valor especificado directamente o una función definida por el usuario. 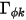 también se determina indirectamente a través de un número de Schmidt especificado, que es un valor especificado o una función definida por el usuario. El número de Schmidt turbulento,
también se determina indirectamente a través de un número de Schmidt especificado, que es un valor especificado o una función definida por el usuario. El número de Schmidt turbulento, 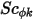 , es una constante especificada por el usuario, con un valor por defecto de uno. El término de origen
, es una constante especificada por el usuario, con un valor por defecto de uno. El término de origen 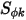 puede ser una constante, una función definida por el usuario en forma de origen por volumen o el origen total en el dominio de cálculo.
puede ser una constante, una función definida por el usuario en forma de origen por volumen o el origen total en el dominio de cálculo.
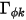 ,
, 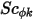 y
y  son el coeficiente de difusión especificado por el usuario, el número de Schmidt turbulento y el término de origen para el escalar
son el coeficiente de difusión especificado por el usuario, el número de Schmidt turbulento y el término de origen para el escalar 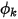 , respectivamente. Aquí
, respectivamente. Aquí 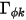 se supone que es isótropo. Puede ser un valor especificado directamente o una función definida por el usuario.
se supone que es isótropo. Puede ser un valor especificado directamente o una función definida por el usuario. 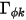 también se determina indirectamente a través de un número de Schmidt especificado, que es un valor especificado o una función definida por el usuario. El número de Schmidt turbulento,
también se determina indirectamente a través de un número de Schmidt especificado, que es un valor especificado o una función definida por el usuario. El número de Schmidt turbulento, 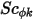 , es una constante especificada por el usuario, con un valor por defecto de uno. El término de origen
, es una constante especificada por el usuario, con un valor por defecto de uno. El término de origen 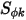 puede ser una constante, una función definida por el usuario en forma de origen por volumen o el origen total en el dominio de cálculo.
puede ser una constante, una función definida por el usuario en forma de origen por volumen o el origen total en el dominio de cálculo.Se debe tener en cuenta que al seleccionar el módulo Especies (Species), solo se añade una ecuación escalar. Para escalares de  , el módulo se debe seleccionar
, el módulo se debe seleccionar 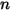 veces y asignar a cada especie un nombre diferente.
veces y asignar a cada especie un nombre diferente.
 , el módulo se debe seleccionar
, el módulo se debe seleccionar 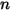 veces y asignar a cada especie un nombre diferente.
veces y asignar a cada especie un nombre diferente.La ecuación 2.376 es una ecuación escalar general. Se puede resolver solo para un transporte escalar o como adición a cualquiera de los módulos estándar o a todos ellos. Puesto que los términos de difusión y origen se determinan por las entradas que el usuario realiza de valores constantes o funciones definidas por el usuario, la ecuación de transporte escalar general se puede utilizar para desarrollar nuevos modelos físicos, tales como los modelos de turbulencia y de combustión. También se puede utilizar en formas reducidas que solo consistan en algunos de los términos de la ecuación. A continuación, se indican algunos ejemplos:
• Ecuación de Poisson y Laplace
En el modo de régimen permanente, si el flujo convectivo no se resuelve o permanece constante, la ecuación 2.376 se reduce a un problema solo de difusión:
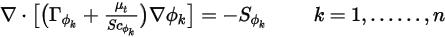
Asimismo, si se desestima la difusión turbulenta ( o
o 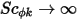 ) y
) y 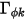 es una constante, la ecuación 2.376 se convierte en una ecuación de Poisson:
es una constante, la ecuación 2.376 se convierte en una ecuación de Poisson:
 o
o 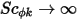 ) y
) y 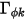 es una constante, la ecuación 2.376 se convierte en una ecuación de Poisson:
es una constante, la ecuación 2.376 se convierte en una ecuación de Poisson:
Y cuando 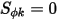 , la ecuación 2.376 escalar se añade además a una ecuación de Laplace.
, la ecuación 2.376 escalar se añade además a una ecuación de Laplace.
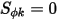 , la ecuación 2.376 escalar se añade además a una ecuación de Laplace.
, la ecuación 2.376 escalar se añade además a una ecuación de Laplace.Entre muchas aplicaciones, si 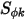 se reemplaza por la densidad de carga de volumen (
se reemplaza por la densidad de carga de volumen (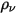 ) y
) y 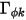 es la permitividad (
es la permitividad (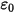 ), se puede aplicar la ecuación 2.376 para calcular el potencial eléctrico (
), se puede aplicar la ecuación 2.376 para calcular el potencial eléctrico ( ) en un campo eléctrico:
) en un campo eléctrico:
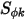 se reemplaza por la densidad de carga de volumen (
se reemplaza por la densidad de carga de volumen (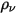 ) y
) y 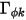 es la permitividad (
es la permitividad (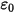 ), se puede aplicar la ecuación 2.376 para calcular el potencial eléctrico (
), se puede aplicar la ecuación 2.376 para calcular el potencial eléctrico ( ) en un campo eléctrico:
) en un campo eléctrico: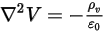
• Transporte convectivo
Sin el término de difusión (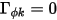 y
y 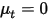 o
o 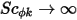 ), la ecuación 2.376 se reduce a:
), la ecuación 2.376 se reduce a:
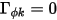 y
y 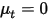 o
o 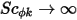 ), la ecuación 2.376 se reduce a:
), la ecuación 2.376 se reduce a: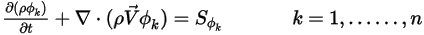
La ecuación 2.376 se puede utilizar para modelar el transporte de fracciones volumétricas de fase (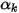 ) en flujos de varias fases, en los que las fases son inmiscibles (consulte el módulo Multifase (Multiphase)):
) en flujos de varias fases, en los que las fases son inmiscibles (consulte el módulo Multifase (Multiphase)):
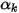 ) en flujos de varias fases, en los que las fases son inmiscibles (consulte el módulo Multifase (Multiphase)):
) en flujos de varias fases, en los que las fases son inmiscibles (consulte el módulo Multifase (Multiphase)):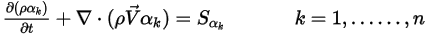
cuando 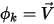 y ⃗
y ⃗ , la ecuación 2.376 representa las ecuaciones de Euler para los flujos no viscosos:
, la ecuación 2.376 representa las ecuaciones de Euler para los flujos no viscosos:
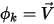 y ⃗
y ⃗ , la ecuación 2.376 representa las ecuaciones de Euler para los flujos no viscosos:
, la ecuación 2.376 representa las ecuaciones de Euler para los flujos no viscosos: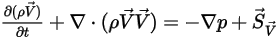
Condiciones de límite
Un escalar definido por el usuario es cualquier cantidad física. Por lo tanto, las condiciones de límite no se definen como condiciones de límite de flujo. Por ejemplo, un límite de entrada de flujo puede significar otra cosa completamente distinta para el escalar 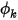 . Como resultado, para la ecuación de transporte escalar general, se pueden aplicar todos los tipos de límite definidos para los límites físicos que se seleccionen.
. Como resultado, para la ecuación de transporte escalar general, se pueden aplicar todos los tipos de límite definidos para los límites físicos que se seleccionen.
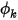 . Como resultado, para la ecuación de transporte escalar general, se pueden aplicar todos los tipos de límite definidos para los límites físicos que se seleccionen.
. Como resultado, para la ecuación de transporte escalar general, se pueden aplicar todos los tipos de límite definidos para los límites físicos que se seleccionen.Si 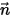 es un vector de unidad normal a la superficie de límite local, la expresión general del flujo másico por unidad de área será:
es un vector de unidad normal a la superficie de límite local, la expresión general del flujo másico por unidad de área será:
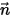 es un vector de unidad normal a la superficie de límite local, la expresión general del flujo másico por unidad de área será:
es un vector de unidad normal a la superficie de límite local, la expresión general del flujo másico por unidad de área será: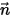
si la advección y la difusión están ambas presentes en el límite.
Para el transporte escalar, 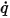 representa el flujo por unidad de área que sale o entra en el dominio físico en un límite. En función de las aplicaciones, las siguientes condiciones de límite comunes se derivan de esta formulación general:
representa el flujo por unidad de área que sale o entra en el dominio físico en un límite. En función de las aplicaciones, las siguientes condiciones de límite comunes se derivan de esta formulación general:
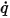 representa el flujo por unidad de área que sale o entra en el dominio físico en un límite. En función de las aplicaciones, las siguientes condiciones de límite comunes se derivan de esta formulación general:
representa el flujo por unidad de área que sale o entra en el dominio físico en un límite. En función de las aplicaciones, las siguientes condiciones de límite comunes se derivan de esta formulación general:• Zero Flux
El flujo por unidad de área a través del límite (normal a él) se especifica en cero. Con la condición de flujo cero,  , los flujos convectivo y difusivo se deben equilibrar con exactitud:
, los flujos convectivo y difusivo se deben equilibrar con exactitud:
 , los flujos convectivo y difusivo se deben equilibrar con exactitud:
, los flujos convectivo y difusivo se deben equilibrar con exactitud: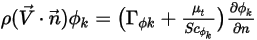
Esto significa que, si un término es cero, el otro término también debe ser cero. Por ejemplo, en un límite sólido (pared), la velocidad normal a la superficie es cero, 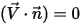 , aunque
, aunque  puede no ser cero. Para satisfacer la restricción de la ecuación 2.376, el gradiente del escalar en el límite debe ser cero,
puede no ser cero. Para satisfacer la restricción de la ecuación 2.376, el gradiente del escalar en el límite debe ser cero, 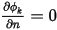 .
.
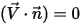 , aunque
, aunque  puede no ser cero. Para satisfacer la restricción de la ecuación 2.376, el gradiente del escalar en el límite debe ser cero,
puede no ser cero. Para satisfacer la restricción de la ecuación 2.376, el gradiente del escalar en el límite debe ser cero, 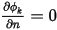 .
.En Creo Flow Analysis, en una pared, el flujo cero es la condición de límite por defecto para el escalar 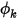 .
.
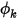 .
.• Valor especificado
El valor especificado es una condición de límite en la que el valor del escalar en el límite, 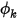 , se determina directamente mediante un valor de entrada del usuario de
, se determina directamente mediante un valor de entrada del usuario de 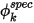 :
:
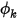 , se determina directamente mediante un valor de entrada del usuario de
, se determina directamente mediante un valor de entrada del usuario de 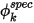 :
:
En Creo Flow Analysis, en una entrada de flujo, el valor constante especificado es la condición de límite por defecto para 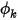 .
.
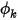 .
.• Simetría
Para una condición de límite de simetría, se aplica un gradiente cero normal al límite para el escalar 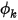 :
:
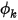 :
: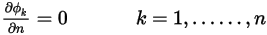
En Creo Flow Analysis, en un límite de simetría de flujo, la simetría también es la condición de límite por defecto para 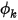 .
.
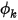 .
.• Salida
La salida se utiliza como una condición de límite en una abertura por donde se espera que el flujo salga o entre en el dominio. Para una salida de presión especificada, una resistencia o un condensador en el flujo, esta es la condición por defecto para el escalar  .
.
 .
.En un límite de salida, la entrada requerida es el valor especificado para el escalar 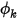 . La condición de límite real aplicada para
. La condición de límite real aplicada para 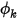 depende de las condiciones de flujo:
depende de las condiciones de flujo:
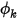 . La condición de límite real aplicada para
. La condición de límite real aplicada para 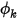 depende de las condiciones de flujo:
depende de las condiciones de flujo:◦ Flujo que sale del dominio: cuando el flujo sale del dominio de cálculo desde una salida o en una entrada mediante flujo inverso, se presupone el valor de gradiente cero en el límite:

◦ Flujo que entra en el dominio: cuando el flujo entra en el dominio de cálculo desde una entrada o en una salida mediante flujo inverso, el valor especificado se aplica al límite:

• Flujo convectivo
En un límite, el flujo convectivo de 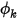 por unidad de área (
por unidad de área (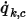 ) se determina como una función del valor de ambiente externo del escalar (
) se determina como una función del valor de ambiente externo del escalar (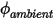 ) y un coeficiente de intercambio (
) y un coeficiente de intercambio (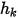 ):
):
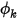 por unidad de área (
por unidad de área (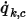 ) se determina como una función del valor de ambiente externo del escalar (
) se determina como una función del valor de ambiente externo del escalar (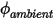 ) y un coeficiente de intercambio (
) y un coeficiente de intercambio (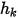 ):
):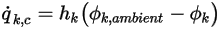
donde 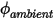 y
y 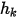 son parámetros de entrada del usuario. Se debe tener en cuenta que el coeficiente de intercambio
son parámetros de entrada del usuario. Se debe tener en cuenta que el coeficiente de intercambio  tiene la unidad de
tiene la unidad de 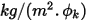 . A partir del flujo convectivo conocido
. A partir del flujo convectivo conocido  , el valor de límite de
, el valor de límite de 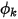 se obtiene con la ecuación 2.376.
se obtiene con la ecuación 2.376.
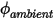 y
y 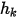 son parámetros de entrada del usuario. Se debe tener en cuenta que el coeficiente de intercambio
son parámetros de entrada del usuario. Se debe tener en cuenta que el coeficiente de intercambio  tiene la unidad de
tiene la unidad de 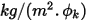 . A partir del flujo convectivo conocido
. A partir del flujo convectivo conocido  , el valor de límite de
, el valor de límite de 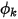 se obtiene con la ecuación 2.376.
se obtiene con la ecuación 2.376.• Flujo escalar especificado
En esta condición de límite, el flujo del escalar se especifica de dos maneras:
◦ Flujo por área: en la ecuación 2.376, el flujo escalar por unidad de área 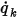 se especifica mediante una entrada del usuario como un valor constante o función definida por el usuario:
se especifica mediante una entrada del usuario como un valor constante o función definida por el usuario:
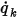 se especifica mediante una entrada del usuario como un valor constante o función definida por el usuario:
se especifica mediante una entrada del usuario como un valor constante o función definida por el usuario:
A continuación, de la ecuación 2.376, se obtiene  en función de las condiciones de flujo.
en función de las condiciones de flujo.
 en función de las condiciones de flujo.
en función de las condiciones de flujo.◦ Flujo total: el flujo escalar total se conoce a través de una entrada de usuario como un valor constante o función definida por el usuario:
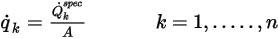
donde  es el flujo escalar total especificado y
es el flujo escalar total especificado y 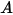 es el área de límite total. A continuación,
es el área de límite total. A continuación, 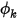 se obtiene de la ecuación 2.376 según las condiciones de flujo.
se obtiene de la ecuación 2.376 según las condiciones de flujo.
 es el flujo escalar total especificado y
es el flujo escalar total especificado y 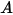 es el área de límite total. A continuación,
es el área de límite total. A continuación, 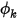 se obtiene de la ecuación 2.376 según las condiciones de flujo.
se obtiene de la ecuación 2.376 según las condiciones de flujo.