Modelo de partícula discreta
En el modelo de partícula discreta, el flujo de la fase dispersa se modela mediante el seguimiento de un número de partículas especificado a través de la fase continua de fluido. En Creo Flow Analysis, en el modelo se incluyen las siguientes suposiciones y restricciones:
• Número definido de partículas esféricas a través de la fase continua de flujo de fluido. Las partículas se definen como Tiene masa (Has Mass) o Sin masa (Massless).
• Un radio especificado en la posición de liberación y el tiempo determinan el tamaño de la partícula, que permanece sin cambios. La interacción partícula-partícula es insignificante.
• Las partículas interactúan con el flujo de fluido y los límites de pared. El volumen de una partícula no desplaza fluido (pocas fracciones volumétricas en la fase de partícula) ni interfiere con la geometría (una partícula de gran tamaño cabe a través de una brecha más pequeña).
• No se produce ninguna transferencia de calor ni masa entre la fase continua de fluido y las partículas. Se supone que la temperatura de la partícula es igual que la temperatura local del flujo de fluido.
En estas condiciones, se realiza el seguimiento del movimiento de cada partícula individual mediante el enfoque Lagrangian. El seguimiento se realiza mediante la formación de un conjunto de ecuaciones diferenciales ordinarias en su momento para cada partícula, que consta de ecuaciones para la posición y la velocidad. Estas ecuaciones se integran para calcular la reacción de las partículas a medida que atraviesan el dominio de flujo. Las características del enfoque de modelado de partículas en Creo Flow Analysis son las siguientes:
• El modelo de partícula discreta sigue el enfoque de Euler-Lagrange. La fase de fluido se trata como un continuo mediante la resolución de la continuidad y las ecuaciones de Navier-Stokes. La fase dispersa se resuelve mediante el seguimiento del movimiento de cada partícula individual utilizando un enfoque lagrangiano. La fracción de volumen que toman las partículas no se incluye en el cálculo de fase continua.
• Las partículas definidas en Sin masa (Massless) se mueven con el flujo de fluido o siguen las líneas de flujo del campo de flujo. El tamaño o el radio de la partícula no afecta al flujo o a las partículas y es solo para visualización.
• Para las partículas definidas en Tiene masa (Has Mass, la masa viene determinada por los valores especificados para el radio o el diámetro de la partícula especificada, así como la densidad de la partícula. Las fuerzas que actúan sobre una partícula, que determinan el movimiento de las partículas, incluyen el arrastre partícula-fluido (fuerza de inercia) y la gravedad. No se tienen en cuenta las fuerzas de dispersión de la turbulencia en las partículas. El tamaño de las partículas influye en las fuerzas de arrastre de partícula-fluido, así como en el postproceso.
• El intercambio de momento entre la fase de fluido y las fases de partículas discretas se modela con los siguientes elementos:
◦ Acoplamiento unidireccional: solo la fase de fluido afecta a los movimientos de las partículas.
◦ Acoplamiento bidireccional: las partículas también afectan al flujo de fluido a través de las fuerzas de arrastre partícula-fluido.
• Las interacciones de partícula y pared se modelan con modelos de pared de partículas como, por ejemplo, adherencia, rebote perfecto y rebote parcial.
• Aunque la fase de fluido puede ser constante y no constante, el seguimiento de partículas es un proceso transitorio que implica la integración de trayectorias de partículas a través del dominio discreto. En este enfoque, las partículas individuales se liberan o inyectan desde ubicaciones especificadas en momentos diferentes. Se realiza un seguimiento de cada partícula desde su posición de liberación hasta el destino, donde escapa al dominio o cumple determinados límites de integración. Por último, se obtiene un promedio de todos los seguimientos de partícula y se calculan las interacciones partícula-fluido como términos de origen para las ecuaciones de momento de fase de fluido.
• La trayectoria recorrida por las partículas aparece con el método de seguimiento de línea de corriente relacionado en el módulo Partícula (Particle).
Teoría del movimiento de partículas
En el enfoque Lagrange, el movimiento de partícula viene determinado por el equilibrio de fuerzas de la partícula y las condiciones en las que se libera la partícula (condiciones iniciales). Para modelar la fase de partículas discretas, se forman primero las ecuaciones de movimiento de las partículas, en función del equilibrio de fuerzas. A continuación, se especifica el límite y las condiciones iniciales para las partículas. Por último, se lleva a cabo la integración de la ecuación de movimiento de la partícula para el seguimiento de partículas.
Ecuaciones de movimiento de las partículas
• Equilibrio de fuerzas de las partículas
En el caso de una partícula discreta que se desplaza en un medio fluido continuo, el movimiento de la partícula viene determinado por la fuerza neta que actúa sobre ella. Según la segunda ley de Newton, se puede expresar el equilibrio de fuerzas en la partícula con el siguiente formato de Lagrange:
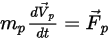
Ecuación 2.366
donde,
 | kg de masa de partícula |
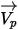 | m/s de velocidad de la partícula |
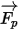 | fuerza neta ejercida en la partícula (N), que afecta a la aceleración de la partícula |
En un sistema de coordenadas cartesiano, si
punto 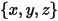 | ubicación de la partícula |
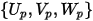 | componentes de la velocidad de partícula |
Con el enfoque de Lagrangian, la velocidad de la partícula 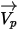 se define como:
se define como:
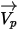 se define como:
se define como: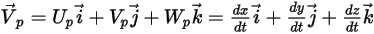
Ecuación 2.367
Para una partícula esférica que ocupa un volumen 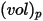 con una densidad
con una densidad 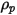 y un diámetro
y un diámetro  (Creo Flow Analysis acepta el radio como entrada), la masa de la partícula
(Creo Flow Analysis acepta el radio como entrada), la masa de la partícula 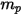 se calcula de la siguiente manera:
se calcula de la siguiente manera:
 con una densidad
con una densidad 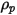 y un diámetro
y un diámetro  (Creo Flow Analysis acepta el radio como entrada), la masa de la partícula
(Creo Flow Analysis acepta el radio como entrada), la masa de la partícula 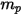 se calcula de la siguiente manera:
se calcula de la siguiente manera: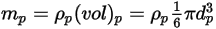
Ecuación 2.368
En cuanto a la fuerza neta 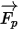 , los factores contribuyentes son, por ejemplo, la fuerza de arrastre de fluido a partícula, el efecto de la gravedad y las fuerzas debidas a la rotación del dominio (fuerzas centrípetas y de Coriolis). Los factores contribuyentes adicionales son otras fuerzas debidas a la diferencia de velocidad entre la partícula y el fluido, así como al desplazamiento del fluido por la partícula. En Creo Flow Analysis
, los factores contribuyentes son, por ejemplo, la fuerza de arrastre de fluido a partícula, el efecto de la gravedad y las fuerzas debidas a la rotación del dominio (fuerzas centrípetas y de Coriolis). Los factores contribuyentes adicionales son otras fuerzas debidas a la diferencia de velocidad entre la partícula y el fluido, así como al desplazamiento del fluido por la partícula. En Creo Flow Analysis 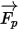 se puede expresar de la siguiente manera:
se puede expresar de la siguiente manera:
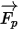 , los factores contribuyentes son, por ejemplo, la fuerza de arrastre de fluido a partícula, el efecto de la gravedad y las fuerzas debidas a la rotación del dominio (fuerzas centrípetas y de Coriolis). Los factores contribuyentes adicionales son otras fuerzas debidas a la diferencia de velocidad entre la partícula y el fluido, así como al desplazamiento del fluido por la partícula. En Creo Flow Analysis
, los factores contribuyentes son, por ejemplo, la fuerza de arrastre de fluido a partícula, el efecto de la gravedad y las fuerzas debidas a la rotación del dominio (fuerzas centrípetas y de Coriolis). Los factores contribuyentes adicionales son otras fuerzas debidas a la diferencia de velocidad entre la partícula y el fluido, así como al desplazamiento del fluido por la partícula. En Creo Flow Analysis 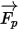 se puede expresar de la siguiente manera:
se puede expresar de la siguiente manera: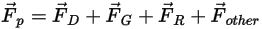
Ecuación 2.369
donde,
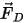 | fuerza de arrastre (N) |
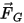 | fuerza de gravedad (N) |
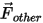 | otras fuerzas, tales como la fuerza másica virtual, la fuerza del gradiente de presión y la fuerza de sustentación especificadas por el usuario (n) |
Por defecto, solo se tiene en cuenta la fuerza de arrastre en la partícula.
Al sustituir la ecuación 2.369 por la ecuación 2.366 y dividirla por  , la ecuación de equilibrio de fuerzas resuelta para una partícula tiene el siguiente formato:
, la ecuación de equilibrio de fuerzas resuelta para una partícula tiene el siguiente formato:
 , la ecuación de equilibrio de fuerzas resuelta para una partícula tiene el siguiente formato:
, la ecuación de equilibrio de fuerzas resuelta para una partícula tiene el siguiente formato: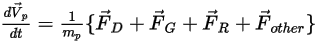
Ecuación 2.370
Para cerrar la ecuación 2.370, se debe calcular la contribución de cada fuerza individual. Los submodelos o las formulaciones adoptadas en Creo Flow Analysis son los siguientes:
◦ Fuerza de arrastre sobre las partículas
La fuerza de arrastre aerodinámica sobre una partícula es proporcional a la velocidad de deslizamiento de fase, la diferencia entre las velocidades de fluido y partícula. Suponiendo que, en el mismo espacio en el que se encuentra la partícula en un momento dado, la velocidad de flujo de fluido es igual a 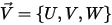 , la fuerza de arrastre se expresa como:
, la fuerza de arrastre se expresa como:
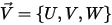 , la fuerza de arrastre se expresa como:
, la fuerza de arrastre se expresa como: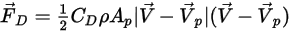
Ecuación 2.371
donde,
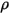 | densidad de fase de fluido |
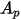 | área de la partícula proyectada en la dirección del flujo |
En el caso de una partícula esférica con el diámetro 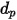 ,
, 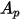 es el área máxima del corte transversal:
es el área máxima del corte transversal:
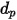 ,
, 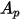 es el área máxima del corte transversal:
es el área máxima del corte transversal: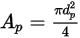
Ecuación 2.372
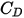 es el coeficiente de arrastre, que depende del número de Reynolds relativo
es el coeficiente de arrastre, que depende del número de Reynolds relativo 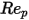 :
: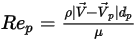
Ecuación 2.373
donde  es la viscosidad dinámica del fluido (PA-s).
es la viscosidad dinámica del fluido (PA-s).
 es la viscosidad dinámica del fluido (PA-s).
es la viscosidad dinámica del fluido (PA-s).Se introduce el coeficiente de arrastre 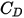 para tener en cuenta los resultados experimentales en el arrastre viscoso de una esfera sólida. Se desarrollan varios modelos o correlaciones empíricas para determinar la función de arrastre
para tener en cuenta los resultados experimentales en el arrastre viscoso de una esfera sólida. Se desarrollan varios modelos o correlaciones empíricas para determinar la función de arrastre 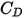 (
(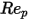 ) y estimar el intercambio fluido-partícula. Para las partículas esféricas suaves, entre muchos modelos, la función
) y estimar el intercambio fluido-partícula. Para las partículas esféricas suaves, entre muchos modelos, la función 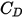 más completa es las correcciones de Morsi y Alexander.
más completa es las correcciones de Morsi y Alexander.
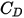 para tener en cuenta los resultados experimentales en el arrastre viscoso de una esfera sólida. Se desarrollan varios modelos o correlaciones empíricas para determinar la función de arrastre
para tener en cuenta los resultados experimentales en el arrastre viscoso de una esfera sólida. Se desarrollan varios modelos o correlaciones empíricas para determinar la función de arrastre 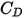 (
(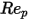 ) y estimar el intercambio fluido-partícula. Para las partículas esféricas suaves, entre muchos modelos, la función
) y estimar el intercambio fluido-partícula. Para las partículas esféricas suaves, entre muchos modelos, la función 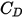 más completa es las correcciones de Morsi y Alexander.
más completa es las correcciones de Morsi y Alexander.Referencias: S. A. Morsi and A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193–208, 26 de septiembre de 1972.
que incluye la expresión general:
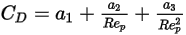
Ecuación 2.374
donde 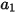 ,
, 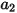 y
y 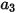 son constantes del modelo cuyos valores dependen del número de Reynolds relativo, como se muestra en la tabla:
son constantes del modelo cuyos valores dependen del número de Reynolds relativo, como se muestra en la tabla:
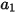 ,
, 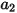 y
y 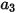 son constantes del modelo cuyos valores dependen del número de Reynolds relativo, como se muestra en la tabla:
son constantes del modelo cuyos valores dependen del número de Reynolds relativo, como se muestra en la tabla: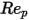 | 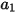 | 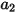 | 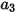 |
0 <  <=0.1 <=0.1 | 0 | 24 | 0 |
0.1 < 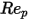 <=1 <=1 | 3.690 | 22.73 | 0.0903 |
1< 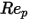 <=10 <=10 | 1.222 | 29.1667 | -3.8889 |
10 < 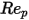 <=100 <=100 | 0.6167 | 46.50 | -116.67 |
100 <  <=1000 <=1000 | 0.3644 | 98.33 | -2778 |
1000 < 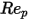 <=5000 <=5000 | 0.357 | 148.62 | -47500 |
5000 <  <=10000 <=10000 | 0.46 | -490.546 | 578700 |
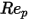 >10000 >10000 | 0.5191 | -1662.5 | 5416700 |
En la tabla se muestra que, en los números de Reynolds de partícula muy bajos (régimen viscoso),  , el coeficiente de arrastre para el flujo que pasa por partículas esféricas vuelve a la ley Stokes:
, el coeficiente de arrastre para el flujo que pasa por partículas esféricas vuelve a la ley Stokes:
 , el coeficiente de arrastre para el flujo que pasa por partículas esféricas vuelve a la ley Stokes:
, el coeficiente de arrastre para el flujo que pasa por partículas esféricas vuelve a la ley Stokes:
Ecuación 2.375
En cambio, si 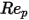 es lo suficientemente grande como para que los efectos de inercia dominen sobre los efectos viscosos, el flujo fluido-partícula se encuentra en la inercia o el régimen de Newton. En la tabla, se observa que el coeficiente de arrastre se vuelve menos dependiente del número de Reynolds relativo. Además, a menudo se utiliza una constante de valor
es lo suficientemente grande como para que los efectos de inercia dominen sobre los efectos viscosos, el flujo fluido-partícula se encuentra en la inercia o el régimen de Newton. En la tabla, se observa que el coeficiente de arrastre se vuelve menos dependiente del número de Reynolds relativo. Además, a menudo se utiliza una constante de valor 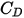 en lugar del modelo completo de Morsi y Alexander:
en lugar del modelo completo de Morsi y Alexander:
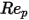 es lo suficientemente grande como para que los efectos de inercia dominen sobre los efectos viscosos, el flujo fluido-partícula se encuentra en la inercia o el régimen de Newton. En la tabla, se observa que el coeficiente de arrastre se vuelve menos dependiente del número de Reynolds relativo. Además, a menudo se utiliza una constante de valor
es lo suficientemente grande como para que los efectos de inercia dominen sobre los efectos viscosos, el flujo fluido-partícula se encuentra en la inercia o el régimen de Newton. En la tabla, se observa que el coeficiente de arrastre se vuelve menos dependiente del número de Reynolds relativo. Además, a menudo se utiliza una constante de valor 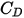 en lugar del modelo completo de Morsi y Alexander:
en lugar del modelo completo de Morsi y Alexander: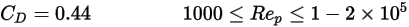
Ecuación 2.376
En la región de transición entre los regímenes viscoso e inercial, 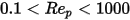 , para partículas esféricas, son importantes tanto los efectos viscosos como inerciales. Por lo tanto, el coeficiente de arrastre es una función compleja del número de Reynolds relativo, que se puede estimar por el modelo de Morsi y Alexander u otras correlaciones. Por ejemplo, según el modelo de Schiller y Naumann:
, para partículas esféricas, son importantes tanto los efectos viscosos como inerciales. Por lo tanto, el coeficiente de arrastre es una función compleja del número de Reynolds relativo, que se puede estimar por el modelo de Morsi y Alexander u otras correlaciones. Por ejemplo, según el modelo de Schiller y Naumann:
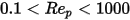 , para partículas esféricas, son importantes tanto los efectos viscosos como inerciales. Por lo tanto, el coeficiente de arrastre es una función compleja del número de Reynolds relativo, que se puede estimar por el modelo de Morsi y Alexander u otras correlaciones. Por ejemplo, según el modelo de Schiller y Naumann:
, para partículas esféricas, son importantes tanto los efectos viscosos como inerciales. Por lo tanto, el coeficiente de arrastre es una función compleja del número de Reynolds relativo, que se puede estimar por el modelo de Morsi y Alexander u otras correlaciones. Por ejemplo, según el modelo de Schiller y Naumann:Referencias: L. Schiller and Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
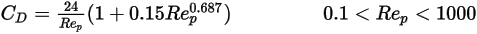
Ecuación 2.377
Para simplificar la expresión del término de fuerza de arrastre en la ecuación 2.370, se introduce el tiempo de relajación de partículas 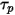 :
:
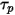 :
: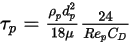
Ecuación 2.378
Si se combina la ecuación 2.368, la ecuación 2.371, la ecuación 2.372, la ecuación 2.373 y la ecuación 2.378, la fuerza de arrastre por masa de partícula de unidad tiene la siguiente formulación:
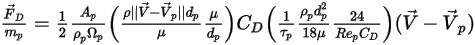
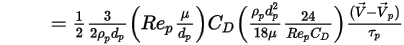
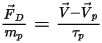
Ecuación 2.379
Por lo tanto, la ecuación de equilibrio de fuerzas de partícula por defecto (solo se considera la fuerza de arrastre) se expresa como:
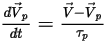
Ecuación 2.380
• Inclusión del término de gravedad
Por defecto, el término de gravedad no se incluye en la ecuación de equilibrio de fuerzas de partículas. Se puede activar el término de gravedad en Creo Flow Analysis. En el caso de una partícula sumergida en flujo de fluido, el efecto de la gravedad da lugar a una fuerza de flotación que es igual al volumen del fluido desplazado por la partícula. Suponiendo que 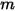 sea la masa de fluido desplazada y
sea la masa de fluido desplazada y 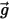 sea el vector de gravedad, la fuerza resultante será la siguiente:
sea el vector de gravedad, la fuerza resultante será la siguiente:
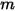 sea la masa de fluido desplazada y
sea la masa de fluido desplazada y 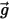 sea el vector de gravedad, la fuerza resultante será la siguiente:
sea el vector de gravedad, la fuerza resultante será la siguiente: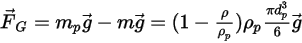
Ecuación 2.381
O bien, la fuerza por masa de partícula de unidad se proporciona como:
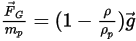
Ecuación 2.382
Y la ecuación de equilibrio de fuerzas tiene el formato:
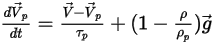
Ecuación 2.383
• Fuerza de rotación sobre las partículas
Para los flujos de fluido de modelo en un marco de referencia rotativa, el término de fuerza adicional inducida por rotación 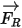 es una parte intrínseca de la aceleración de partículas. Consta del efecto de las fuerzas de Coriolis y centrípeta:
es una parte intrínseca de la aceleración de partículas. Consta del efecto de las fuerzas de Coriolis y centrípeta:
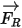 es una parte intrínseca de la aceleración de partículas. Consta del efecto de las fuerzas de Coriolis y centrípeta:
es una parte intrínseca de la aceleración de partículas. Consta del efecto de las fuerzas de Coriolis y centrípeta: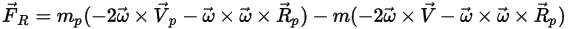
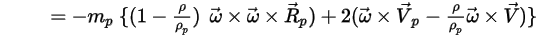
Ecuación 2.384
O bien, la fuerza de rotación por masa de partícula de unidad se proporciona como:
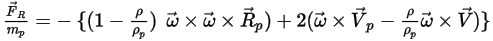
Ecuación 2.385
donde,
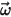 | velocidad angular del marco de referencia rotativo |
 | vector que conecta el centro del eje y la ubicación de la partícula |
Con la adición de este término de fuerza, la ecuación de equilibrio de partículas es:

Ecuación 2.386
La ecuación 2.386 gobierna el movimiento de una partícula en un sistema Lagrange cuando el flujo se resuelve en un marco de referencia rotativa.
Condiciones de límite e iniciales de las partículas
En el método Lagrange, el seguimiento de partículas es un procedimiento transitorio. Por lo tanto, se requieren las condiciones de límite e iniciales para calcular las trayectorias de las partículas. Las condiciones de límite definen la reacción de la partícula en los límites del dominio computacional, especialmente de las interacciones partícula-pared. Las condiciones iniciales determinan la liberación de partículas desde los límites, incluida la posición de liberación, la frecuencia, la velocidad, el tipo y el tamaño (radio) de la partícula y el número de partículas.
Condiciones de límite
Creo Flow Analysis proporciona una condición de límite de fase discreta para determinar la reacción de las partículas en un límite. Cuando una partícula alcanza un límite del dominio de flujo (incluido el límite físico y la interfaz sólido-fluido), por ejemplo, una pared o un límite de entrada, se produce una de las siguientes situaciones:
• La partícula se refleja a través de una colisión elástica o inelástica.
• La partícula se escapa a través del límite y desaparece del cálculo en el punto de impacto con el límite.
• La partícula se atrapa en la pared y desaparece del cálculo en el punto de impacto con el límite.
• La partícula pasa a través de una zona de límite interna, como un ventilador o un obstáculo poroso.
• La interacción partícula-límite viene determinada por métodos definidos por el usuario para modelar la reacción de la partícula cuando alcanza el límite.
Según la reacción de la partícula en los límites, las condiciones de límite de flujo y las interfaces se reagrupan en tres tipos de condiciones de límite de partículas discretas: abierto, de simetría y de pared.
• Límite abierto de partícula discreta
Las partículas o líneas de flujo pueden salir del dominio computacional. Un límite abierto es un límite de entrada o salida de la fase de flujo de fluido en el sistema de Euler. También se puede aplicar a los límites de flujo, tales como pared y simetría. En un límite abierto de partícula, esta sale o entra en el dominio en función de la dirección de velocidad de la partícula.
Supongamos que 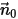 es el vector normal de unidad al límite abierto que apunta fuera del dominio computacional, con la velocidad de límite de partícula
es el vector normal de unidad al límite abierto que apunta fuera del dominio computacional, con la velocidad de límite de partícula 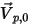 . Si
. Si  , el vector de velocidad
, el vector de velocidad 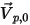 apunta fuera del dominio computacional. Esto indica que la partícula se escapa a través del límite y desaparece del cálculo en el punto de impacto con el límite.
apunta fuera del dominio computacional. Esto indica que la partícula se escapa a través del límite y desaparece del cálculo en el punto de impacto con el límite.
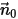 es el vector normal de unidad al límite abierto que apunta fuera del dominio computacional, con la velocidad de límite de partícula
es el vector normal de unidad al límite abierto que apunta fuera del dominio computacional, con la velocidad de límite de partícula 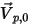 . Si
. Si  , el vector de velocidad
, el vector de velocidad 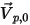 apunta fuera del dominio computacional. Esto indica que la partícula se escapa a través del límite y desaparece del cálculo en el punto de impacto con el límite.
apunta fuera del dominio computacional. Esto indica que la partícula se escapa a través del límite y desaparece del cálculo en el punto de impacto con el límite.• Límite de partícula de simetría
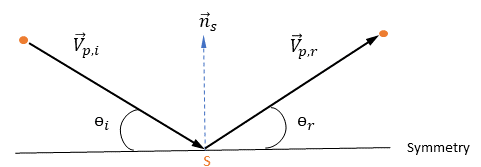
Cuando una partícula o línea de corriente del dominio computacional alcanza un límite de simetría discreto, la condición de límite lo refleja de nuevo en el dominio. Para la fase de partícula discreta, un límite de partícula de simetría se corresponde normalmente con una simetría de flujo en el sistema de Euler. También puede ser una ubicación para la liberación de la partícula.
Supongamos que 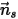 sea el vector normal de unidad a simetría en el punto
sea el vector normal de unidad a simetría en el punto 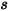 de la simetría y que su dirección apunte fuera de la simetría hacia el dominio computacional.
de la simetría y que su dirección apunte fuera de la simetría hacia el dominio computacional. 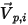 y
y 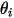 se introducen para indicar el ángulo de velocidad de impacto de la partícula en el límite de simetría de partículas, tal como se muestra en la siguiente figura. Cuando la partícula se refleja desde la simetría, se conserva su energía cinética total: la velocidad tangencial permanece igual mientras que el componente de velocidad normal solo cambia de signo. La condición de límite de simetría de partículas se expresa como:
se introducen para indicar el ángulo de velocidad de impacto de la partícula en el límite de simetría de partículas, tal como se muestra en la siguiente figura. Cuando la partícula se refleja desde la simetría, se conserva su energía cinética total: la velocidad tangencial permanece igual mientras que el componente de velocidad normal solo cambia de signo. La condición de límite de simetría de partículas se expresa como:
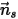 sea el vector normal de unidad a simetría en el punto
sea el vector normal de unidad a simetría en el punto 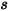 de la simetría y que su dirección apunte fuera de la simetría hacia el dominio computacional.
de la simetría y que su dirección apunte fuera de la simetría hacia el dominio computacional. 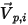 y
y 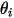 se introducen para indicar el ángulo de velocidad de impacto de la partícula en el límite de simetría de partículas, tal como se muestra en la siguiente figura. Cuando la partícula se refleja desde la simetría, se conserva su energía cinética total: la velocidad tangencial permanece igual mientras que el componente de velocidad normal solo cambia de signo. La condición de límite de simetría de partículas se expresa como:
se introducen para indicar el ángulo de velocidad de impacto de la partícula en el límite de simetría de partículas, tal como se muestra en la siguiente figura. Cuando la partícula se refleja desde la simetría, se conserva su energía cinética total: la velocidad tangencial permanece igual mientras que el componente de velocidad normal solo cambia de signo. La condición de límite de simetría de partículas se expresa como:
Ecuación 2.387
donde,
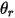 | ángulo en el punto 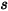 : de la simetría (grados) : de la simetría (grados) |
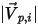 | magnitud de la velocidad de incidencia de la partícula (m/s) |
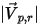 | magnitud de la velocidad de reflexión de la partícula (m/s) |
• Límite de partícula de pared
Para las gotas líquidas, la interacción gota-pared depende de la temperatura de la pared, el material y la rugosidad de la pared, el ángulo y la velocidad del impacto, la existencia de una película en la pared y otros parámetros. Como resultado, se utiliza un rango de submodelos para reproducir los distintos regímenes de interacciones pared-partícula y tener en cuenta los efectos de los parámetros de flujo y las condiciones de límite de pared.
En el modelo de partícula discreta actual, se supone que la forma, el tamaño y la masa de las partículas permanecen sin cambios. Asimismo, se considera que el fluido y las partículas se encuentran en el equilibrio térmico. Por lo tanto, en un enfoque sencillo se describe el proceso de las partículas (con masa) que colisionan con paredes: durante el proceso de colisión, las partículas intercambian el momento solo con la pared y tienen tres formas de interactuar con la pared. Las tres formas son el rebote perfecto, el rebote de adherencia y el rebote parcial.

◦ Rebote perfecto: una partícula o línea de corriente se refleja cuando alcanza una pared. El momento y la energía cinética de la partícula se conservan perfectamente. El ángulo de incidencia es igual al ángulo de reflexión, mientras que el componente de velocidad normal a pared cambia de signo:

Ecuación 2.388
donde,
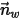 | vector normal de unidad a pared |
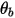 | ángulo en el límite de pared (grados) |
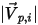 | magnitud de la velocidad de incidencia de la partícula (m/s) |
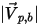 | magnitud de la velocidad de rebote de la partícula (m/s) |
◦ Adherencia: una partícula colisiona con la pared, pierde todo su momento y energía, y se adhiere a la pared:
Sin tener en cuenta la acumulación de partículas a lo largo de la pared, la partícula desaparece por completo del cálculo en el punto de impacto con el límite.
◦ Rebote parcial: condición de partícula de pared entre el rebote perfecto y la adherencia. Una partícula o línea de corriente rebota desde una pared, pero pierde parte de la energía en una dirección normal, tangencial o ambas. El momento y la energía cinética de la partícula no se conservan y el ángulo de incidencia suele ser mayor que el ángulo de reflexión:
La pérdida de energía a través de la interacción partícula-pared se especifica mediante las entradas del usuario:
▪ Pérdida de energía normal: se especifica la pérdida del componente normal de la energía cinética de una partícula en la pared.
▪ Pérdida de energía tangencial: se especifica la pérdida del componente tangencial de la energía cinética de una partícula en la pared.
En Creo Flow Analysis, se determina si una partícula rebota o se adhiere mediante los valores especificados de las velocidades normales máxima y mínima. Suponiendo que  es la velocidad normal máxima de partícula especificada y
es la velocidad normal máxima de partícula especificada y  es la velocidad normal mínima de la partícula especificada, existen las siguientes condiciones:
es la velocidad normal mínima de la partícula especificada, existen las siguientes condiciones:
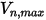 es la velocidad normal máxima de partícula especificada y
es la velocidad normal máxima de partícula especificada y 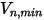 es la velocidad normal mínima de la partícula especificada, existen las siguientes condiciones:
es la velocidad normal mínima de la partícula especificada, existen las siguientes condiciones:▪ Si 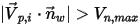 o
o 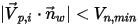 , la partícula rebota desde la pared.
, la partícula rebota desde la pared.
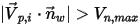 o
o 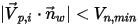 , la partícula rebota desde la pared.
, la partícula rebota desde la pared.▪ Si  , la partícula se adhiere a la pared.
, la partícula se adhiere a la pared.
 , la partícula se adhiere a la pared.
, la partícula se adhiere a la pared.Los modelos de interacción partícula-pared solo se aplican a las partículas definidas en Tiene masa (Has Mass). Una partícula sin masa sigue la línea de flujo del flujo a lo largo de las paredes.
Se debe tener en cuenta que los límites de pared de partícula pueden ser paredes externas e interfaces fluido-sólido. Como en los límites de partícula abiertos y de simetría, las partículas se pueden liberar desde un límite de pared.
Condiciones iniciales (liberar partículas)
Las condiciones iniciales proporcionan los valores iniciales para todas las variables de fase discreta dependientes que describen las condiciones instantáneas de una partícula individual. En el seguimiento de partículas del sistema Lagrange, el procedimiento para determinar las condiciones iniciales implican liberaciones de partículas (frecuencia y distribuciones) desde los límites (abierto, de simetría, de pared y de interfaz) y la asignación de propiedades para cada partícula.
Cuando se activa Liberar partícula (Release Particle), los siguientes parámetros o variables son las condiciones iniciales de los movimientos de partícula:
Integración de la ecuación de movimiento de partículas
Para realizar el seguimiento del movimiento de partículas, las ecuaciones de trayectoria de cada partícula se resuelven (integran) de forma analítica o numérica en un sistema Lagrange. En la ecuación 2.367 y la ecuación 2.386, las ecuaciones de movimiento se reescriben como:
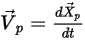
Ecuación 2.391
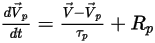
Ecuación 2.392
donde,
 | vector de posición de la partícula |
 | incluye aceleraciones debidas a todas las demás fuerzas, excepto la fuerza de arrastre, como la gravedad, los efectos de la rotación, etc. |
La ecuación 2.391 y la ecuación 2.392 son un conjunto de ecuaciones diferenciales ordinarias asociadas. Con las condiciones inicial y de límite dadas, el desplazamiento de la partícula, ecuación 2.391, se calcula mediante la integración de Euler de avance de la velocidad de la partícula en el paso de tiempo, 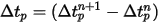 :
:
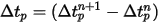 :
: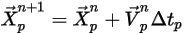
Ecuación 2.393
donde,
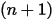 | nuevos valores |
 | valores actuales |
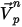 | velocidad de la partícula en el paso de tiempo actual |
En el primer paso de tiempo,
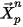 | posición de liberación |
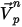 | velocidad inicial |
donde,

Ecuación 2.394
En este método de integración de avance, se presupone que la velocidad de partícula calculada al principio del paso de tiempo prevalece sobre todo el paso. Al final del paso de tiempo, la nueva velocidad de partícula se calcula mediante la resolución de la ecuación 2.392 de momento de partícula. Suponiendo que 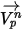 ,
, 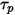 y
y 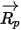 sean constantes durante un período de tiempo
sean constantes durante un período de tiempo 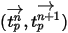 y las propiedades de fluido se tomen del inicio del paso de tiempo del tiempo
y las propiedades de fluido se tomen del inicio del paso de tiempo del tiempo  , se dispone de la solución analítica de la ecuación 2.392:
, se dispone de la solución analítica de la ecuación 2.392:
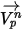 ,
, 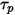 y
y 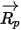 sean constantes durante un período de tiempo
sean constantes durante un período de tiempo 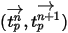 y las propiedades de fluido se tomen del inicio del paso de tiempo del tiempo
y las propiedades de fluido se tomen del inicio del paso de tiempo del tiempo  , se dispone de la solución analítica de la ecuación 2.392:
, se dispone de la solución analítica de la ecuación 2.392: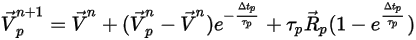
Ecuación 2.395
Para evaluar 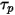 y
y  , se requieren variables de fluido como la densidad, la viscosidad y la velocidad en la posición de la partícula. Se consideran valores de celda de la fase de flujo de fluido en la que se encuentra la partícula actualmente. Aunque este esquema analítico sea eficiente, puede ser inexacto para pasos de tiempo grandes y en situaciones en las que las partículas no se encuentren en el equilibrio hidrodinámico con el flujo de fluido continuo. En este caso, los esquemas numéricos integran la ecuación 2.392.
, se requieren variables de fluido como la densidad, la viscosidad y la velocidad en la posición de la partícula. Se consideran valores de celda de la fase de flujo de fluido en la que se encuentra la partícula actualmente. Aunque este esquema analítico sea eficiente, puede ser inexacto para pasos de tiempo grandes y en situaciones en las que las partículas no se encuentren en el equilibrio hidrodinámico con el flujo de fluido continuo. En este caso, los esquemas numéricos integran la ecuación 2.392.
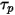 y
y  , se requieren variables de fluido como la densidad, la viscosidad y la velocidad en la posición de la partícula. Se consideran valores de celda de la fase de flujo de fluido en la que se encuentra la partícula actualmente. Aunque este esquema analítico sea eficiente, puede ser inexacto para pasos de tiempo grandes y en situaciones en las que las partículas no se encuentren en el equilibrio hidrodinámico con el flujo de fluido continuo. En este caso, los esquemas numéricos integran la ecuación 2.392.
, se requieren variables de fluido como la densidad, la viscosidad y la velocidad en la posición de la partícula. Se consideran valores de celda de la fase de flujo de fluido en la que se encuentra la partícula actualmente. Aunque este esquema analítico sea eficiente, puede ser inexacto para pasos de tiempo grandes y en situaciones en las que las partículas no se encuentren en el equilibrio hidrodinámico con el flujo de fluido continuo. En este caso, los esquemas numéricos integran la ecuación 2.392.Acoplamiento de partícula-fluido
En el enfoque de Euler-Lagrange, se supone que el flujo de fluido continuo afecta a la reacción de la partícula a través de fuerzas, calor y transferencia de masa. Por ejemplo, el término de fuerza 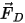 en la ecuación 2.370 del equilibrio de fuerzas de la partícula se refiere a la fuerza de arrastre aerodinámico del flujo en la partícula. Aunque la fase de partícula se considere discreta y no desplace el fluido en el volumen, las partículas pueden ejercer una influencia compensatoria en el flujo de fluido a través de los intercambios de momento y, posiblemente, de masa y calor. El efecto de las partículas en el flujo se conoce como acoplamiento de partícula-fluido. Tiene dos categorías:
en la ecuación 2.370 del equilibrio de fuerzas de la partícula se refiere a la fuerza de arrastre aerodinámico del flujo en la partícula. Aunque la fase de partícula se considere discreta y no desplace el fluido en el volumen, las partículas pueden ejercer una influencia compensatoria en el flujo de fluido a través de los intercambios de momento y, posiblemente, de masa y calor. El efecto de las partículas en el flujo se conoce como acoplamiento de partícula-fluido. Tiene dos categorías:
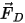 en la ecuación 2.370 del equilibrio de fuerzas de la partícula se refiere a la fuerza de arrastre aerodinámico del flujo en la partícula. Aunque la fase de partícula se considere discreta y no desplace el fluido en el volumen, las partículas pueden ejercer una influencia compensatoria en el flujo de fluido a través de los intercambios de momento y, posiblemente, de masa y calor. El efecto de las partículas en el flujo se conoce como acoplamiento de partícula-fluido. Tiene dos categorías:
en la ecuación 2.370 del equilibrio de fuerzas de la partícula se refiere a la fuerza de arrastre aerodinámico del flujo en la partícula. Aunque la fase de partícula se considere discreta y no desplace el fluido en el volumen, las partículas pueden ejercer una influencia compensatoria en el flujo de fluido a través de los intercambios de momento y, posiblemente, de masa y calor. El efecto de las partículas en el flujo se conoce como acoplamiento de partícula-fluido. Tiene dos categorías:• Acoplamiento unidireccional
El acoplamiento unidireccional permite al fluido influir en las trayectorias de las partículas, pero las partículas no tienen ningún efecto sobre el fluido. Para las partículas sin masa, la interacción partícula-fluido es un acoplamiento unidireccional: las partículas se mueven junto con el flujo de fluido. En el caso de las partículas que tienen masa, el acoplamiento unidireccional puede ser una aproximación aceptable en flujos con cargas de fase poco dispersas, donde las partículas tienen una influencia insignificante en el flujo de fluido.
Para la fase continua de fluido, el campo de flujo se calcula como un flujo de fluido de una sola fase sin la existencia de una fase de partícula dispersa. A continuación, se realiza el seguimiento del movimiento de la partícula según el flujo calculado archivado y las condiciones iniciales. Para un flujo en régimen permanente, el seguimiento de la partícula se produce después de que se obtenga la solución de flujo convergente de la fase continua mediante la resolución de las ecuaciones de continuidad y de Navier-Stokes. En el caso de una simulación de flujo transitorio, se realiza un seguimiento de los movimientos de la partícula al final de cada paso de tiempo de la simulación de flujo.
• Acoplamiento bidireccional
En el caso de las partículas con masa, el acoplamiento bidireccional permite que el fluido influya en las trayectorias de las partículas. También se tiene en cuenta para el efecto de las partículas en la fase continua de fluido. Sin la inclusión de la transferencia de masa y calor, la interacción bidireccional entre el fluido y las partículas solo se refiere al intercambio de momento. Para el momento transferido desde la fase continua a la fase discreta, se calcula mediante el seguimiento del momento obtenido o perdido por cada partícula individual a medida que pasan a través de un volumen de control. En el acoplamiento bidireccional, los intercambios de momento partícula-fluido deben incluirse en las ecuaciones de momento de fluido para tener en cuenta el efecto de las trayectorias de fase discreta en el continuo. A partir de la ecuación 2.386, se deduce que solo la fuerza de arrastre se tiene en cuenta para el intercambio de momento partícula-fluido y se añade en las ecuaciones de momento. Se debe tener en cuenta que, para las partículas sin masa, no se calcula ningún término de intercambio entre el flujo de fluido y ellas, de modo que, las trayectorias de fase discreta no tienen ningún impacto en el continuo.
Para incluir los efectos del arrastre partícula-fluido en las ecuaciones de momento de fase continua, la fuerza de arrastre de cada partícula que se mueve a través del flujo se aplica en el volumen de control donde se encuentra la partícula durante el paso de tiempo. Para la partícula 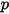 , se calcula su origen de momento debido a
, se calcula su origen de momento debido a 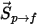 de arrastre a partir de la siguiente ecuación diferencial:
de arrastre a partir de la siguiente ecuación diferencial:
 , se calcula su origen de momento debido a
, se calcula su origen de momento debido a  de arrastre a partir de la siguiente ecuación diferencial:
de arrastre a partir de la siguiente ecuación diferencial: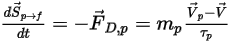
Ecuación 2.396
Y el origen de la partícula para la fase continua es el término de origen 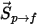 que se multiplica por el caudal de la partícula (el caudal de masa dividido por la masa de la partícula):
que se multiplica por el caudal de la partícula (el caudal de masa dividido por la masa de la partícula):
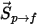 que se multiplica por el caudal de la partícula (el caudal de masa dividido por la masa de la partícula):
que se multiplica por el caudal de la partícula (el caudal de masa dividido por la masa de la partícula):
Ecuación 2.397
donde,
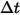 | paso de tiempo |
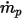 | caudal de masa de partículas |
Suponiendo que 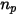 sea el número de partículas que pasan a través de un volumen de control en el paso de tiempo
sea el número de partículas que pasan a través de un volumen de control en el paso de tiempo 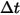 , se dispone del término de origen de partícula a fluido total:
, se dispone del término de origen de partícula a fluido total:
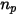 sea el número de partículas que pasan a través de un volumen de control en el paso de tiempo
sea el número de partículas que pasan a través de un volumen de control en el paso de tiempo 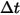 , se dispone del término de origen de partícula a fluido total:
, se dispone del término de origen de partícula a fluido total: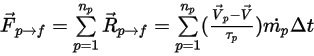
Ecuación 2.398
Con la adición de la fuerza de arrastre fluido-partícula, las ecuaciones gobernantes que se resuelven para la fase continua se expresan ahora como:

Ecuación 2.399

Ecuación 2.400
Con el acoplamiento unidireccional, la fase continua de fluido  está gobernada por las ecuaciones exactas de continuidad y momento de fase única. Para el acoplamiento bidireccional, se tiene el término de origen de fuerza de arrastre de partícula a fluido adicional. La ecuación 2.399 y la ecuación 2.400 se resuelven igual que el flujo de una sola fase.
está gobernada por las ecuaciones exactas de continuidad y momento de fase única. Para el acoplamiento bidireccional, se tiene el término de origen de fuerza de arrastre de partícula a fluido adicional. La ecuación 2.399 y la ecuación 2.400 se resuelven igual que el flujo de una sola fase.
 está gobernada por las ecuaciones exactas de continuidad y momento de fase única. Para el acoplamiento bidireccional, se tiene el término de origen de fuerza de arrastre de partícula a fluido adicional. La ecuación 2.399 y la ecuación 2.400 se resuelven igual que el flujo de una sola fase.
está gobernada por las ecuaciones exactas de continuidad y momento de fase única. Para el acoplamiento bidireccional, se tiene el término de origen de fuerza de arrastre de partícula a fluido adicional. La ecuación 2.399 y la ecuación 2.400 se resuelven igual que el flujo de una sola fase.