ODE ソルバー
それぞれが境界およびボリュームの 1 自由度の直線移動および回転を制御する常微分方程式 (ODE) である式 2.432と式 2.444は、Creo Flow Analysis で数値的に計算されます。具体的には、境界およびボリュームの移動と変位を計算するには、次の時間進行スキームを採用して ODE 式を積分します。スティフ、オイラー、ルンゲ-クッタ陽的ソルバー。
1 自由度の直線移動式の積分
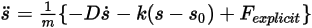
式 2.455
ここで、明示的に計算されたフォース項 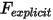 は次のようになります。
は次のようになります。
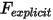 は次のようになります。
は次のようになります。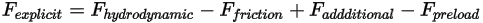
式 2.456
与えられた初期条件と境界条件では、陽的な時間進行スキームを使用して式 2.455を積分することで剛体の変位を取得できます。時間ステップ 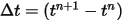 に対して次のような一般式が得られます。
に対して次のような一般式が得られます。
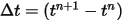 に対して次のような一般式が得られます。
に対して次のような一般式が得られます。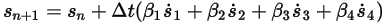
式 2.457
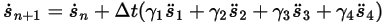
式 2.458
ここで、ウェイト係数の合計は 1 です。
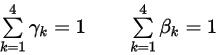
式 2.459
ウェイト係数の選択肢があるので、各種のスキームが導出されます。たとえば、オイラーおよびルンゲ-クッタ陽的スキームは次に従います。
• オイラー陽的ソルバー (1 次)
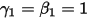 および
および 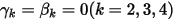 の場合、次のようなオイラー陽的スキームが得られます。
の場合、次のようなオイラー陽的スキームが得られます。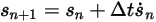
式 2.460
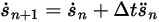
式 2.461
• ルンゲ-クッタ陽的ソルバー
ルンゲ-クッタソルバーは、次に従う 2 次および 4 次の陽的スキームです。
◦ 2 次スキーム
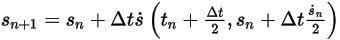
式 2.462
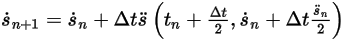
式 2.463
◦ 4 次スキーム
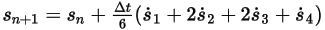
式 2.464
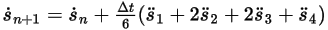
式 2.465
ここで、

式 2.466

式 2.467

式 2.468

式 2.469
• スティフソルバー (陽的)
標準のオイラーおよびルンゲ-クッタスキームに加えて、Creo Flow Analysis では直線移動の 1 自由度 ODE 式を積分するためのスティフソルバーが開発されています。これは剛体の動的運動を計算するデフォルトの方法です。
1 自由度の回転式の積分
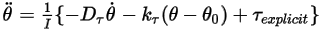
式 2.470
ここで、明示的に計算されたトルク項 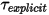 は次のようになります。
は次のようになります。
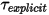 は次のようになります。
は次のようになります。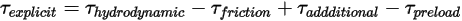
式 2.471
与えられた初期条件と境界条件では、陽的な時間進行スキームを使用して式 2.470を積分することで回転の角度を取得できます。時間ステップ 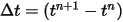 に対して次のような一般式が得られます。
に対して次のような一般式が得られます。
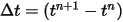 に対して次のような一般式が得られます。
に対して次のような一般式が得られます。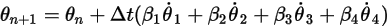
式 2.472
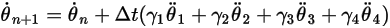
式 2.473
ここで、ウェイト係数の合計は 1 です。
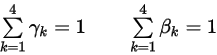
式 2.474
ウェイト係数の選択肢があるので、各種の数値スキームが容易に導出されます。同じように、オイラーおよびルンゲ-クッタ陽的スキームは次のように与えられます。
• オイラー陽的ソルバー (1 次)
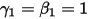 および
および 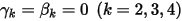 の場合、次のようなオイラー陽的スキームが得られます。
の場合、次のようなオイラー陽的スキームが得られます。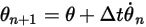
式 2.475
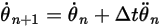
式 2.476
• ルンゲ-クッタ陽的ソルバー
ルンゲ-クッタソルバーは、次のように与えられる 2 次および 4 次の陽的スキームです。
◦ 2 次スキーム
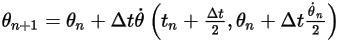
式 2.477
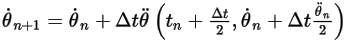
式 2.478
◦ 4 次スキーム
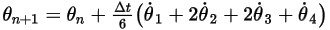
式 2.479
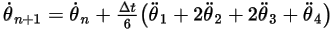
式 2.480
ここで、

式 2.481

式 2.482

式 2.483

式 2.484
• スティフソルバー (陽的)
標準のオイラーおよびルンゲ-クッタスキームに加えて、Creo Flow Analysis では 1 自由度の回転 ODE 式である式 2.444を積分するためのスティフソルバーが開発されています。これは剛体の動的運動を計算するデフォルトの方法です。
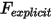 にグループ化して簡略化することで、1 自由度の運動の直線移動式を次の形式でに書き換えます。
にグループ化して簡略化することで、1 自由度の運動の直線移動式を次の形式でに書き換えます。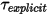 にグループ化して簡略化することで、1 自由度の運動の回転式である
にグループ化して簡略化することで、1 自由度の運動の回転式である