剛体の運動
シミュレーションでは、ソリッドオブジェクトのサーフェスは通常、流れドメイン内の壁面境界になります。ソリッドオブジェクトまたはサーフェスが、動的なフォースならびに機械的なフォースと熱的な影響を受ける場合、ネットフォースの不均衡によってボディが移動および変形する場合があります。流れシミュレーションでは、ソリッドオブジェクトが剛体と見なされることがよくあります。このため、フォースの不均衡の影響を受けるソリッドオブジェクトは、変形することなく、線形に移動 (直線移動) または特定の角度に移動 (回転移動) するか、その両方に移動する可能性があります。ただし、CFA 計算ドメインでは、境界移動によってドメインの変更につながることがあり、その場合は流れモジュールで説明したように、ボリュームメッシュが変形する可能性があります。
剛体の運動を制御する方程式は、線形運動量と角運動量の保存から直接求められます。
• 線形運動量 (直線移動)
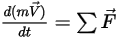
式 2.426
• 角運動量 (回転移動)
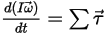
式 2.427
式 2.426において、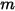
は移動オブジェクトの質量であり、
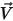は線形/遷移速度であり、
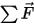は直線移動中のボディにかかる合計/ネットフォースです。式 2.427において、
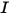は慣性モーメントであり、
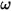⃗ は角速度であり、
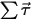⃗ は回転中のボディに作用する合計/ネットトルクです。
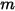は移動オブジェクトの質量であり、 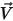は線形/遷移速度であり、 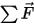は直線移動中のボディにかかる合計/ネットフォースです。式 2.427において、 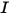は慣性モーメントであり、⃗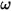 は角速度であり、⃗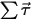 は回転中のボディに作用する合計/ネットトルクです。式 2.426および 式 2.427によって制御される剛体の一般運動の自由度は 6 (6-DOF) で、それぞれ直線移動の自由度が 3 (3-DOF)、回転の自由度が 3 (3-DOF) です。Creo Flow Analysis では、1 自由度の直線移動と回転移動のみを考慮に入れます。これについて、このセクションで説明します。
1 自由度の直線移動
単位ベクトル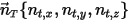 
で定義された任意の指定方向 (変更なし) に剛体が線形移動するとした場合、ボディの直線移動の自由度は 1 (1-DOF) に低下します。その結果、線形運動量の保存では移動速度およびフォースが 
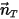で表されるため、式 2.426が移動方向に従ったスカラー式になります。
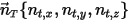で定義された任意の指定方向 (変更なし) に剛体が線形移動するとした場合、ボディの直線移動の自由度は 1 (1-DOF) に低下します。その結果、線形運動量の保存では移動速度およびフォースが 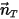で表されるため、式 2.426が移動方向に従ったスカラー式になります。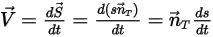
式 2.428
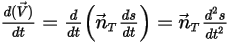
式 2.429
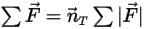
式 2.430
ここで、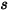
は移動方向 
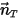に沿った剛体の特定位置での位置ベクトル 
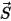のマグニチュードです。直交座標系では、次のようになります。
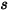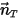は移動方向 に沿った剛体の特定位置での位置ベクトル 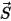のマグニチュードです。直交座標系では、次のようになります。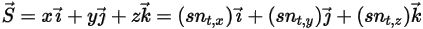
式 2.431
剛体の質量が一定のままとなる場合、ボディにかかるすべてのフォースを明示的に含むようにフォース項を展開すると、スカラー線形運動量式は次のようになります。
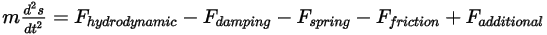
式 2.432
右側のフォースは次を示します。
• 流体力 
- 圧力とせん断力から成り、流体流れと、流れと接触している剛体のサーフェスの間の相対運動によって生じます。圧力とせん断力は流れソリューション (出力量) から得られます。
- 圧力とせん断力から成り、流体流れと、流れと接触している剛体のサーフェスの間の相対運動によって生じます。圧力とせん断力は流れソリューション (出力量) から得られます。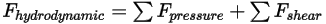
式 2.433
• 減衰力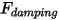 
- 摩擦減衰効果によって生じる制動力。剛体の運動とユーザー定義の減衰係数 
によって決まります。
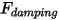- 摩擦減衰効果によって生じる制動力。剛体の運動とユーザー定義の減衰係数 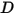によって決まります。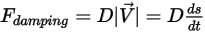
式 2.434
• ばねフォース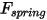 
- ばね変位 
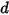、ばね定数 
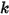、ばね初期荷重フォース 
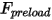に依存します。
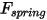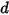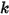- ばね変位 、ばね定数 、ばね初期荷重フォース 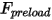に依存します。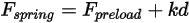
式 2.435
ここで、ばね変位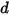 
は次のとおりに定義されます。
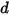は次のとおりに定義されます。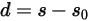
式 2.436
ここで、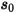
は前の位置 
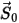での位置ベクトル 
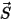のマグニチュードです。
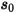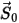は前の位置 での位置ベクトル 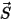のマグニチュードです。• 摩擦力 - 接触摩擦モデルは、動的システムでの摩擦効果を考慮に入れるために採用されています。摩擦力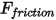 
は次のとおりにモデル化されます。
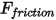は次のとおりにモデル化されます。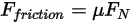
式 2.437
ここで、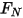
は、対象のソリッドサーフェスにかかる接触フォースの法線成分です。摩擦係数 
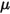については、さらに不動オブジェクトと移動オブジェクトのそれぞれに対して、静摩擦係数 
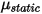と滑り摩擦係数 
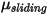が導入されています。
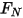は、対象のソリッドサーフェスにかかる接触フォースの法線成分です。摩擦係数 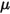については、さらに不動オブジェクトと移動オブジェクトのそれぞれに対して、静摩擦係数 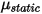と滑り摩擦係数 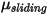が導入されています。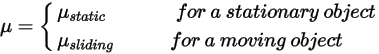
式 2.438
• その他のフォース 
- その他のユーザー指定フォースが追加されています。
- その他のユーザー指定フォースが追加されています。1 自由度の回転
特定の点 (軸の中心) 
と方向単位ベクトル 
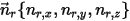によって任意の回転軸が定義されている場合、軸 
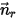を中心とした剛体の回転の自由度も 1 に低下します。同様に、角運動量の保存でも、式 2.427が接線方向 
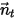に沿ったスカラー式になり、次のように定義されます。
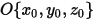と方向単位ベクトル 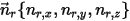によって任意の回転軸が定義されている場合、軸 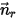を中心とした剛体の回転の自由度も 1 に低下します。同様に、角運動量の保存でも、式 2.427が接線方向 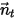に沿ったスカラー式になり、次のように定義されます。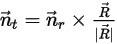
式 2.439
ここで、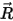
は、軸の中心から剛体上の任意の点 
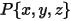を指すベクトルです。
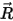は、軸の中心から剛体上の任意の点 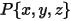を指すベクトルです。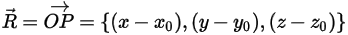
式 2.440
この点 
での角速度およびトルクは、次の式に書き換えることができます。
での角速度およびトルクは、次の式に書き換えることができます。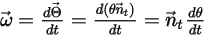
式 2.441
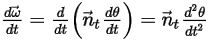
式 2.442
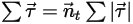
式 2.443
ここで、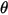
は、開始位置または参照位置に対する点 
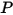の回転角度です。
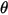は、開始位置または参照位置に対する点 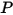の回転角度です。慣性モーメントが一定のままとなる場合、回転ボディにかかるすべてのトルクを明示的に含むようにトルク項を展開すると、スカラー角運動量式は次のようになります。
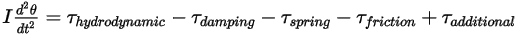
式 2.444
右側のトルク項は次のとおりに定義されます。
• 流体トルク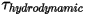 
- 圧力とせん断力によるトルクの組み合わせ。
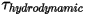- 圧力とせん断力によるトルクの組み合わせ。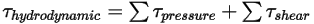
式 2.445
• 減衰トルク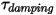 
- 回転速度 
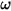とユーザー定義の減衰係数 
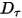に依存します。
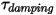- 回転速度 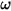とユーザー定義の減衰係数 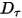に依存します。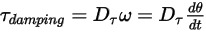
式 2.446
• ばねトルク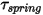 
- 変位角 
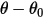、ユーザー定義の初期荷重トルク 
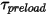、ねじれ定数 
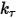に依存するねじれによって生じるトルク。
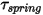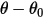- 変位角 、ユーザー定義の初期荷重トルク 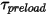、ねじれ定数 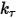に依存するねじれによって生じるトルク。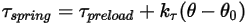
式 2.447
ここで、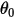
は参照角度です。これは通常、モデルセットアップ中の境界またはボリュームの位置になりますが、異なる位置に対応することもできます。たとえば、ゼロ角変位では、参照角 
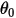は初期角度位置と同一ではありません。
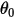は参照角度です。これは通常、モデルセットアップ中の境界またはボリュームの位置になりますが、異なる位置に対応することもできます。たとえば、ゼロ角変位では、参照角 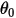は初期角度位置と同一ではありません。• 摩擦トルク - 接触した 2 つのオブジェクトが移動するときに生じる摩擦力によって引き起こされるトルク。実験では、これは適用されたトルクと観察されたトルク/ネットトルクの差異によって決まります。摩擦係数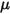 
と、接触サーフェスに適用される垂直フォース 
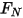による接触トルクに依存します。
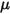と、接触サーフェスに適用される垂直フォース 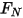による接触トルクに依存します。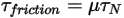
式 2.448
ここで、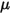
は、式 2.438で定義されたユーザー定義パラメータです。
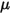は、式 2.438で定義されたユーザー定義パラメータです。• その他のトルク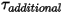 
- その他のユーザー指定トルクが追加されています。
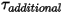- その他のユーザー指定トルクが追加されています。バウンスモデル
多くの場合、剛体の直線移動スペースあるいは回転スペースは制限されます (距離もしくは角度の制限)。または、直線移動スペースと回転スペースの両方が制限されます。つまり、最大位置あるいは最小位置を持つか、またはその両方を持ちます。たとえば、次の図に示すように、単純な重力振子が角度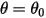 
で元の位置から解放された場合、その質量に作用する回復フォースにより振子が均衡位置を中心に振動します。均衡位置のどちらか一方の最大角度 
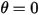は、リリース位置 
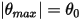に依存します。摩擦がない場合 (摩擦なしピボットで真空)、最大角度は変わらず、振子が同じ最大位置で永遠に前後に振動します。ただし、振子が大気中にある場合、空気抵抗 (減衰) によって時間とともに最大振動角度が減少し、最終的には均衡位置で停止します。
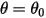で元の位置から解放された場合、その質量に作用する回復フォースにより振子が均衡位置を中心に振動します。均衡位置のどちらか一方の最大角度 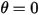は、リリース位置 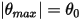に依存します。摩擦がない場合 (摩擦なしピボットで真空)、最大角度は変わらず、振子が同じ最大位置で永遠に前後に振動します。ただし、振子が大気中にある場合、空気抵抗 (減衰) によって時間とともに最大振動角度が減少し、最終的には均衡位置で停止します。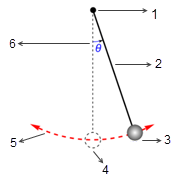
図
1. 摩擦なしピボット
2. 質量のないロッド
3. 非常に大きいおもり
4. 均衡位置
5. おもりの軌道
6. 振幅
さらに、振動サイクル (周期) において振子が最大位置 
に達すると、運動エネルギーが完全に失われて振子の方向が変わります。単純な重力振子では運動エネルギーは完全に位置エネルギーに変わりますが、媒体の抵抗を考慮に入れると、粘性減衰を克服するために運動エネルギーの一部が失われます。ただし、運動エネルギー (速度) が最大で位置が最低のとき、ネットフォースまたは位置エネルギーによって、振子が均衡位置に向かって反対の方向に動き始めます。このケースでは、
によって、1 自由度の角運動量 式 2.444 にはバウンス条件がないことが示されます。
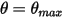に達すると、運動エネルギーが完全に失われて振子の方向が変わります。単純な重力振子では運動エネルギーは完全に位置エネルギーに変わりますが、媒体の抵抗を考慮に入れると、粘性減衰を克服するために運動エネルギーの一部が失われます。ただし、運動エネルギー (速度) が最大で位置が最低のとき、ネットフォースまたは位置エネルギーによって、振子が均衡位置に向かって反対の方向に動き始めます。このケースでは、 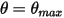によって、1 自由度の角運動量 式 2.444 にはバウンス条件がないことが示されます。バウンス条件がないことに加えて、制限された位置で移動するボディは、運動エネルギーをまったく失わずにはね返るか (完全バウンス)、一部の運動エネルギーのみを失う (部分バウンス) 場合があります。このため、1 自由度の直線移動および回転の力学方程式、式 2.432および式 2.444を計算して、流れドメインに対する剛体または壁面境界の運動を決定するとき、次の 3 つのバウンス条件が提供されます。
• バウンスなし - Creo Flow Analysis のデフォルトモデル。このモデルでは、剛体または境界が運動の限界に達すると、運動エネルギーがすべて失われて方向が変わります。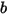
と 
がバウンスおよび入射を表し、
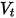と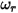 
が直線移動および回転速度 (マグニチュードのみ) を表すとき、このバウンスモデルは次のように表されます。
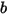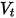と がバウンスおよび入射を表し、 と 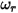が直線移動および回転速度 (マグニチュードのみ) を表すとき、このバウンスモデルは次のように表されます。◦ 直線移動
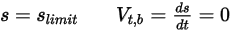
式 2.449
◦ 回転
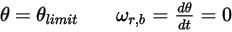
式 2.450
• 部分バウンス - このモデルでは、剛体または境界が運動の限界に達すると、ユーザー指定係数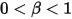 
によって決まる一部の運動エネルギーが失われて方向が変わります。
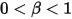によって決まる一部の運動エネルギーが失われて方向が変わります。◦ 直線移動
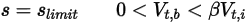
式 2.451
◦ 回転
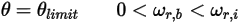
式 2.452
• 完全バウンス - このモデルでは、剛体または境界が運動の限界に達すると、運動エネルギー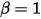 
がまったく失われずに方向が変わります。
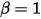がまったく失われずに方向が変わります。◦ 直線移動
直線移動
◦ 回転
直線移動