関数
「定義式エディタ」(Expression Editor) の以下の関数を使用して、ベクトルとスカラーの算術操作と論理処理を行うことができます。
• 演算子
◦ ベクトルとスカラーに共通 (加算や減算など)
◦ スカラーのみ (平方根や対数など)
◦ ベクトルのみ (ドット積やクロス積など)
• 論理
• 三角関数と双曲線関数
• その他の関数
• テーブル
演算子
演算子を使用してベクトルとスカラー両方の算術操作を行えます。以下の表で、a、b、c はスカラーであり、U、V、W はベクトルです。
|
定義式演算子
|
関数
|
例
|
|---|---|---|
|
演算子: スカラー/ベクトル
|
||
|
足し算
|
a = b+c または V = U+W
|
|
|
引き算
|
a = b-c または V = U-W
|
|
|
*
|
2 つのスカラーの乗算、または 1 つのスカラーと 1 つのベクトルの乗算
|
a = b*c または V = a*U (ただし V = U * W ではない)
|
|
演算子: スカラーのみ
|
||
|
/
|
割り算
|
a = b/c
|
|
exp(scalar)
|
e を底とした指数関数
|
a= exp(b) は e の b 乗: a= eb
|
|
ln(scalar)
|
e を底とする自然対数関数
|
a= ln(b) は b の自然対数を返す
|
|
sqrt(scalar)
|
平方根関数
|
a = sqrt(b)
|
|
^
|
指数関数
|
a= b^c は b の c 乗: a= bc
|
|
演算子: ベクトルのみ
|
||
|
&
|
ベクトルドット積
|
a = V&U (a = |V| |U| cos (angle))
|
|
^
|
ベクトルクロス積
|
V=U^W (|V| = |U| |W| x sin (angle) 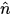 )、右手の法則が適用されます。 )、右手の法則が適用されます。 |
|
len(vector)
|
ベクトル V の長さを返す
|
a = len(V)
|
|
normalize(vector)
|
正規化された単位ベクトル V/|V| を返す
|
V = normalize(U)
|
|
rotate(vector,angle, direction,center)
|
回転角度、右手の法則、回転軸、およびオプションの回転中心に基づいて回転後のベクトルを返します (中心が定義されていない場合、デフォルトで 0,0,0 になります)。
|
Vrot = rotate(V,alpha,U,W) ここで V は回転の対象となるベクトル、alpha は角度 (ラジアン)、U は回転軸です。右手の法則が適用されます。W はベクトルとして定義されているオプションの中心点です。
|
論理
論理関数では論理文を取り込むことができます。
|
定義式演算子
|
関数
|
例
|
|---|---|---|
|
true
|
論理真
|
|
|
false
|
論理偽
|
|
|
<
|
より小さい
|
|
|
>
|
より大きい
|
|
|
==
|
論理比較で等しい
|
a = (b==3) ? 1 : 2
|
|
または
|
論理和
|
|
|
および
|
論理積
|
|
|
!
|
論理否定
|
!< より小さくない
|
|
a = expression ? b : c
|
a = b (定義式が真の場合)
a = c (定義式が偽の場合)
|
a = (b>3) ? 1 : 2 ==> (b が 3 より大きい場合は a = 1、そうでない場合は a = 2)
|
三角関数と双曲線関数
三角関数と双曲線関数では対応する関数を算術文に取り込むことができます。
|
超越定義式
|
関数
|
|---|---|
|
三角関数
|
|
|
sin(radians)
|
正弦関数
|
|
cos(radians)
|
余弦関数
|
|
cot(radians)
|
余接関数
|
|
tan(radians)
|
正接関数
|
|
asin ()
|
逆正弦関数、値をラジアンで返す
|
|
acos ()
|
逆余弦関数、値をラジアンで返す
|
|
acot()
|
逆余接関数、値をラジアンで返す
|
|
atan ()
|
逆正接関数、値をラジアンで返す
|
|
atan2(y,x)
|
2 変数逆性正接関数、(-pi, pi)、値をラジアンで返す
|
|
双曲線関数
|
|
|
sinh ()
|
双曲線正弦関数
|
|
cosh ()
|
双曲線余弦関数
|
|
coth()
|
双曲線余接関数
|
|
tanh ()
|
双曲線正接関数
|
|
asinh()
|
逆双曲線正弦関数
|
|
acosh()
|
逆双曲線余弦関数
|
|
acoth()
|
逆双曲線余接関数
|
|
atanh()
|
逆双曲線正接関数
|
表示関連関数
表示関連関数は表示パネルに関連します。次の操作を実行できます。
• 派生変数のすべての機能を備えた新しい変数が作成できるようになります。これらの機能には、境界やアイソサーフェスなどのジオメトリエンティティにその関数を表示する機能が含まれています。
• 監視点の変数にアクセスします
• XY プロットのユーザー変数を定義します
3D 表示のユーザー定義変数
display.varname - 3D プロットのコンター、アイソサーフェス、ベクトルなどのユーザー変数を定義します。「ビュー」(View) タブの「変数」(Variable) の下の「プロパティ」(Properties) パネルに新しい変数が表示されます。
#display.varname: dispname [unit] - (オプション) ユーザー定義の表示変数の新しい名前と単位を定義します。
例:
display.pref = flow.P - 101325
#display.pref: ゲージ圧力 [Pa]
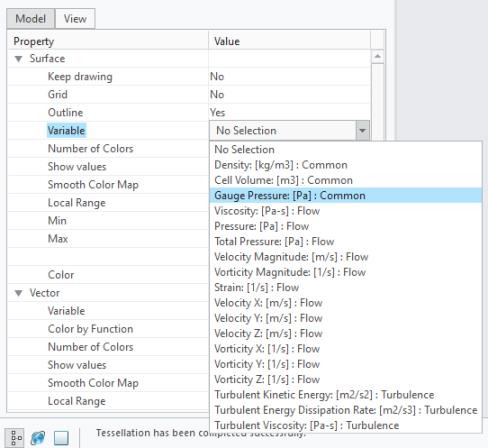
これらの定義式を使用すると、以下に示すように、「変数」(Variable) プロパティの値の下にゲージ圧力エンティティが表示されます。
監視点の変数
以下のフォーマットを使用して、任意の監視点のローカルセル変数にアクセスできます。
module[.subname].var@probe.name
点の座標:
probe.coord@probe_name
例:
inletP = flow.P@probe."Point01"+101325
XY プロットのユーザー定義変数
plot.varname - XY プロットで使用可能なユーザー変数を定義します。新しい共通変数が「プロパティ」(Properties) パネルの「変数」(Variable) プロパティの値として追加されます。
#plot.varname: dispname [unit] - (オプション) ユーザー定義変数の新しい名前と単位を定義します。
例:
plot.head = (flow.pt@outlet - flow.pt@inlet)/998/9.8
#plot.head: 圧力ヘッド [m]
• 新しい表示変数またはプロット変数の名前と単位を定義する際に、コロンシンボルの前にスペースを追加しないでください。 • 表示変数とプロット変数のデフォルト単位が角括弧内に表示されます。たとえば、圧力変数にはデフォルト単位 Pa が表示されます。単位を適切に定義すると、その単位が画面に表示されます。この例では、表示される最終単位を変更すると、その値も変換されます。単位を適切に定義していない場合、その単位は無視されます。 |
その他の関数
定義式演算子 | 関数 | 例 |
|---|---|---|
abs(x) | 絶対値関数 | |
max(x,y) | 最大関数 | a = max(b,c) ==> a= b (b >c の場合) または a=c (c>=b の場合) |
min(x,y) | 最小関数 | a = min(b,c) ==> a= b (b <c の場合) または a=c (c<=b の場合) |
mod(x,y) | 剰余関数 | a = mod(c,b) ==> a = c を b で割ったときの余り |
sgn(x) | 符号を示すフラグ (-1、0、または 1) を返す | a= sgn(b) ==> a = -1 (b<0 の場合) a = 0 (b=0 の場合) a = 1 (b>0 の場合) |
step(x) | ステップ関数、ゼロを基準にして値に応じて 0 または 1 を返す | a= step(b) ==> a = 0 (b<0 の場合) a = 1 (b>=0 の場合) |
テーブル
テーブル関数では、プロジェクトファイル (*.spro) と同じディレクトリ内にある外部テーブルファイルからデータを取り込むことができます。
テーブル定義式 | 関数 |
|---|---|
table(filename,x) | 1D テーブルから補間 |
table(filename, x ,y) | 2D テーブルから補間 |
例:
テーブルの使用:
# テーブルから情報を抽出
p = table("inlet_pressure.txt",time)
density = table("R134a_density.txt",temp,pre)
• テーブルフォーマット: 1D (filename,x) - プロジェクトファイル (*.spro) と同じディレクトリ内にある 1D データテーブルにアクセスできます。
◦ 一様分布の 1D テーブルのフォーマット
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
<table size="n" min="xmin" max="xmax" outside="flat | extrapolation">
# comments (x assumed to have uniform distribution)
v1
v2
...
vn
</table/>
◦ 非一様分布の 1D テーブルのフォーマット
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
<table size="n" outside="flat | extrapolation">
# You can add comments by putting the hashmark “#” in front .. but do not insert comments before the xml line (line 1)
x1 v1
x2 v2
xn vn
</table/>
このフォーマットでは、テーブルタグの下の outside = “flat” or outside = "extrapolation" によって、入力 x, y が範囲外の場合の値の決定方法が指定されています。
• テーブルフォーマット: 2D (filename,x) - プロジェクトファイル (*.spro) と同じディレクトリ内にある 2D データテーブルにアクセスできます。
◦ 一様分布の 2D テーブルのフォーマット
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" min="xmin ymin" max="xmax ymax" outside="flat | extrapolation">
# comment
# values table (x and y assumed to have uniform distribution
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
◦ 非一様分布の 2D テーブルのフォーマット
<?xml version="1.0" encoding="ISO-8859-1"?>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
<table size="nx my" outside ="flat | extrapolation">
# x and y variable ranges
x1 x2 … xn
y1 y2 … ym
# values table
v(x1,y1) v(x2,y1) … v(xn,y1)
v(x1,y2) v(x2,y2) … v(xn,y2)
...
v(x1,ym) v(x2,ym) … v(xn,ym)
</table>
このフォーマットでは、テーブルタグの下の outside = “flat” or outside = "extrapolation" によって、入力 x, y が範囲外の場合の値の決定方法が指定されています。
コメントを追加するには、テキストの前にハッシュ記号 "#" を付けます。xml 行や先頭行の前にコメントを挿入しないでください。 |