離散粒子モデル
離散粒子モデルでは、分散相の流れは、連続流体相を通る、指定した数の粒子を追跡することによってモデル化されます。Creo Flow Analysis では、モデルには以下の推定と制限があります。
• 連続流体流れ相を通る球形粒子は一定数です。粒子は「質量あり」(Has Mass) または「質量なし」(Massless) として定義されます。
• リリース位置および時間における指定半径によって粒子のサイズが決定され、これは変更されません。粒子間相互作用はごくわずかです。
• 粒子は流体流れおよびウォール境界と相互作用します。粒子のボリュームは、流体を変位させたり (粒子相の体積分率が低い)、ジオメトリに干渉したり (過大粒子がより小さいギャップを通り抜ける) しません。
• 連続流体相と粒子の間では、熱伝達と質量移動は発生しません。粒子温度は流体流れのローカル温度と同じであると推定されます。
これらの推定に基づき、個々の粒子の運動はラグランジュ的手法を使用して追跡されます。追跡は、粒子ごとに、位置および速度の式で構成される一連の時間の常微分方程式を形成することによって実行されます。次に、これらの式を積分して、流れドメインを横断するときの粒子の反力が計算されます。Creo Flow Analysis での粒子モデリング手法の特性は以下のとおりです。
• 離散粒子モデルは、オイラー-ラグランジュ的手法に従います。流体相は、連続方程式とナビエ-ストークス方程式を解くことによって連続体として扱われます。分散相は、ラグランジュ的手法を使用して個々の粒子の運動を追跡することによって計算されます。粒子がとる体積分率は、連続相の計算には含まれません。
• 「質量なし」(Massless) に設定されている粒子は、流体流れとともに移動するか、流れ場の流線に従います。粒子のサイズまたは半径は、流れまたは粒子に影響を与えず、表示のみを目的としています。
• 「質量あり」(Has Mass) に設定されている粒子の場合、質量は、指定した粒子の半径または直径と粒子密度によって決定されます。粒子の運動を決定する、粒子に作用するフォースには、粒子-流体牽引 (慣性力) と重力が含まれます。粒子上の乱流分散フォースは考慮されません。粒子のサイズは、粒子-流体抵抗力とポストプロセスに影響を当てます。
• 流体相と離散粒子相の間の運動量交換は、以下のようにモデル化されます。
◦ 一方向結合 - 流体相のみが粒子の運動に影響を与えます。
◦ 双方向結合 - 粒子も、粒子-流体抵抗力を解して流体流れに影響を与えます。
• ウォール-粒子相互作用は、付着、完全反射、部分反射などの粒子ウォールモデルを使用してモデル化されます。
• 流体相は定常であったり非定常であったりしますが、粒子の追跡は非定常プロセスであり、このプロセスでは離散化されたドメインを通る粒子のパスの統合が行われます。この手法では、個々の粒子は、指定した位置から異なる時間にリリースまたは射出されます。各粒子は、そのリリース位置からリリース先まで追跡され、そこでドメインから脱出するか、特定の積分制限を満たします。最後に、すべての粒子の追跡の平均が取得され、粒子-流体相互作用が流体相の運動量方程式に対するソース項として計算されます。
• 粒子が移動したパスは、「粒子」(Particle) モジュールの関連する流線追跡方法を使用して表示されます。
粒子運動理論
ラグランジュ的手法では、粒子の運動は、粒子上のフォースバランスと粒子がリリースされる条件 (初期条件) によって決定されます。離散粒子相をモデル化するには、まずフォースバランスに基づいて粒子の運動方程式を形成します。次に、境界と粒子の初期条件を指定します。最後に、粒子を追跡するための粒子の運動方程式の積分が行われます。
粒子の運動方程式
• 粒子のフォースバランス
連続流体媒体内を移動する離散粒子の場合、粒子の運動は、それに作用するネットフォースによって決定されます。ニュートンの第 2 法則に従って、次のラグランジュの形式で粒子上のフォースバランスを表すことができます。
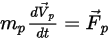
式 2.366
ここで、
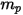 | 粒子質量 (kg) |
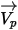 | 粒子速度 (m/s) |
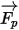 | 粒子加速度に影響を与える、粒子に加えられるネットフォース (N) |
直交座標系では、
点 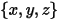 | 粒子の位置 |
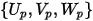 | 粒子速度の成分 |
ラグランジュ的手法では、粒子速度 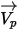 は次のように定義されます。
は次のように定義されます。
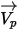 は次のように定義されます。
は次のように定義されます。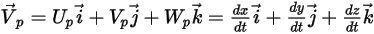
式 2.367
密度 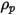 および直径
および直径 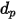 (Creo Flow Analysis は半径を入力として受け入れる) でボリューム
(Creo Flow Analysis は半径を入力として受け入れる) でボリューム 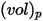 を占める球状粒子の場合、粒子質量
を占める球状粒子の場合、粒子質量 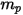 は次のように計算されます。
は次のように計算されます。
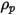 および直径
および直径 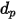 (Creo Flow Analysis は半径を入力として受け入れる) でボリューム
(Creo Flow Analysis は半径を入力として受け入れる) でボリューム 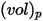 を占める球状粒子の場合、粒子質量
を占める球状粒子の場合、粒子質量 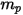 は次のように計算されます。
は次のように計算されます。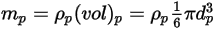
式 2.368
ネットフォース 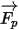 については、流体-粒子抵抗力、重力の影響、ドメインの回転によるフォース (求心力とコリオリの力) などが寄与因子です。その他の寄与因子には、粒子と流体の速度の違いや、粒子による流体の変位を原因とするフォースなどがあります。Creo Flow Analysis では、
については、流体-粒子抵抗力、重力の影響、ドメインの回転によるフォース (求心力とコリオリの力) などが寄与因子です。その他の寄与因子には、粒子と流体の速度の違いや、粒子による流体の変位を原因とするフォースなどがあります。Creo Flow Analysis では、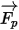 は次のように表すことができます。
は次のように表すことができます。
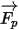 については、流体-粒子抵抗力、重力の影響、ドメインの回転によるフォース (求心力とコリオリの力) などが寄与因子です。その他の寄与因子には、粒子と流体の速度の違いや、粒子による流体の変位を原因とするフォースなどがあります。Creo Flow Analysis では、
については、流体-粒子抵抗力、重力の影響、ドメインの回転によるフォース (求心力とコリオリの力) などが寄与因子です。その他の寄与因子には、粒子と流体の速度の違いや、粒子による流体の変位を原因とするフォースなどがあります。Creo Flow Analysis では、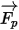 は次のように表すことができます。
は次のように表すことができます。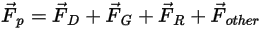
式 2.369
ここで、
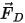 | 抵抗力 (N) |
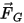 | 重力 (N) |
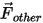 | ユーザーによって指定された仮想質量力、気圧傾度力、揚力などのその他のフォース (n) |
デフォルトでは、粒子上の抵抗力のみが考慮されます。
式 2.369を式 2.366に代入し、それを 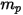 で割ると、計算された粒子のフォースバランスの式は次の形式になります。
で割ると、計算された粒子のフォースバランスの式は次の形式になります。
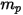 で割ると、計算された粒子のフォースバランスの式は次の形式になります。
で割ると、計算された粒子のフォースバランスの式は次の形式になります。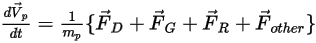
式 2.370
式 2.370を閉じるには、個々のフォースの寄与を計算しなければなりません。Creo Flow Analysis で採用されているサブモデルまたは式は次のとおりです。
◦ 粒子上の抵抗力
粒子上の流線型抵抗力は、流体速度と粒子速度の差である位相スリップの速度に比例します。粒子が所定の時間に位置している空間で、流体の流速が 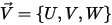 に等しいとすると、抵抗力は次のように表されます。
に等しいとすると、抵抗力は次のように表されます。
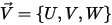 に等しいとすると、抵抗力は次のように表されます。
に等しいとすると、抵抗力は次のように表されます。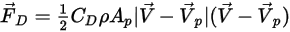
式 2.371
ここで、
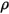 | 流体相の密度 |
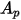 | 流れ方向に投影された粒子の面積 |
直径が 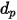 の球状粒子の場合、
の球状粒子の場合、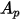 が 2 次元断面の最大面積です。
が 2 次元断面の最大面積です。
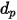 の球状粒子の場合、
の球状粒子の場合、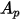 が 2 次元断面の最大面積です。
が 2 次元断面の最大面積です。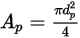
式 2.372
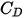 はドラッグ係数で、これは相対的 Reynolds 数
はドラッグ係数で、これは相対的 Reynolds 数 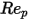 によって異なります。
によって異なります。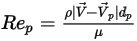
式 2.373
ここで、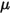 は流体の動粘度 (Pa-s) です。
は流体の動粘度 (Pa-s) です。
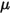 は流体の動粘度 (Pa-s) です。
は流体の動粘度 (Pa-s) です。ドラッグ係数 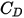 は、固体球の粘性抵抗の実験結果を考慮するために使用されています。流体-粒子交換を推定するドラッグ関数
は、固体球の粘性抵抗の実験結果を考慮するために使用されています。流体-粒子交換を推定するドラッグ関数 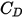 (
(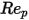 ) を決定するために、さまざまなモデルまたは経験的相関が開発されています。多くのモデルのうち、スムーズな球状粒子の最も完全な
) を決定するために、さまざまなモデルまたは経験的相関が開発されています。多くのモデルのうち、スムーズな球状粒子の最も完全な 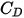 関数は、Morsi と Alexander による相関です。
関数は、Morsi と Alexander による相関です。
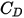 は、固体球の粘性抵抗の実験結果を考慮するために使用されています。流体-粒子交換を推定するドラッグ関数
は、固体球の粘性抵抗の実験結果を考慮するために使用されています。流体-粒子交換を推定するドラッグ関数 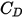 (
(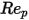 ) を決定するために、さまざまなモデルまたは経験的相関が開発されています。多くのモデルのうち、スムーズな球状粒子の最も完全な
) を決定するために、さまざまなモデルまたは経験的相関が開発されています。多くのモデルのうち、スムーズな球状粒子の最も完全な 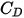 関数は、Morsi と Alexander による相関です。
関数は、Morsi と Alexander による相関です。参照: S. A. Morsi and A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193-208, September 26 1972.
その一般式は次のとおりです。
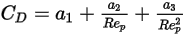
式 2.374
ここで、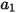 、
、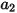 、および
、および 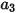 はモデル定数であり、次の表に示すように、その値は相対的 Reynolds 数によって異なります。
はモデル定数であり、次の表に示すように、その値は相対的 Reynolds 数によって異なります。
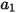 、
、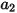 、および
、および 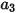 はモデル定数であり、次の表に示すように、その値は相対的 Reynolds 数によって異なります。
はモデル定数であり、次の表に示すように、その値は相対的 Reynolds 数によって異なります。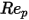 | 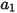 | 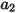 | 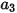 |
0 < 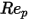 <=0.1 <=0.1 | 0 | 24 | 0 |
0.1 < 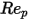 <=1 <=1 | 3.690 | 22.73 | 0.0903 |
1< 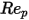 <=10 <=10 | 1.222 | 29.1667 | -3.8889 |
10 < 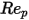 <=100 <=100 | 0.6167 | 46.50 | -116.67 |
100 < 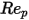 <=1000 <=1000 | 0.3644 | 98.33 | -2778 |
1000 < 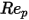 <=5000 <=5000 | 0.357 | 148.62 | -47500 |
5000 < 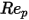 <=10000 <=10000 | 0.46 | -490.546 | 578700 |
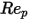 >10000 >10000 | 0.5191 | -1662.5 | 5416700 |
次の表は、Stokes の法則によると、粒子の Reynolds 数 (粘性方式) が非常に低い場合 (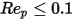 )、流れ通過球状粒子のドラッグ係数が返ることを示しています。
)、流れ通過球状粒子のドラッグ係数が返ることを示しています。
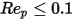 )、流れ通過球状粒子のドラッグ係数が返ることを示しています。
)、流れ通過球状粒子のドラッグ係数が返ることを示しています。
式 2.375
反対に、慣性効果が粘性効果を支配するほど 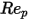 が大きい場合、流体-粒子流れは慣性またはニュートン方式です。この表から、ドラッグ係数の相対的 Reynolds 数への依存が減ることがわかります。また、完全な Morsi と Alexander のモデルの代わりに、
が大きい場合、流体-粒子流れは慣性またはニュートン方式です。この表から、ドラッグ係数の相対的 Reynolds 数への依存が減ることがわかります。また、完全な Morsi と Alexander のモデルの代わりに、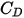 値の定数がよく使用されています。
値の定数がよく使用されています。
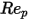 が大きい場合、流体-粒子流れは慣性またはニュートン方式です。この表から、ドラッグ係数の相対的 Reynolds 数への依存が減ることがわかります。また、完全な Morsi と Alexander のモデルの代わりに、
が大きい場合、流体-粒子流れは慣性またはニュートン方式です。この表から、ドラッグ係数の相対的 Reynolds 数への依存が減ることがわかります。また、完全な Morsi と Alexander のモデルの代わりに、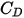 値の定数がよく使用されています。
値の定数がよく使用されています。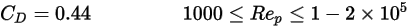
式 2.376
粘性方式と慣性方式の間の遷移領域 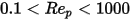 では、球状粒子にとって粘性効果と慣性効果の両方が重要です。したがって、ドラッグ係数は相対的 Reynolds 数の複雑な関数であり、これは Morsi と Alexander のモデルまたはその他の相関によって推定できます。たとえば、Schiller と Naumann のモデルによると、
では、球状粒子にとって粘性効果と慣性効果の両方が重要です。したがって、ドラッグ係数は相対的 Reynolds 数の複雑な関数であり、これは Morsi と Alexander のモデルまたはその他の相関によって推定できます。たとえば、Schiller と Naumann のモデルによると、
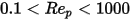 では、球状粒子にとって粘性効果と慣性効果の両方が重要です。したがって、ドラッグ係数は相対的 Reynolds 数の複雑な関数であり、これは Morsi と Alexander のモデルまたはその他の相関によって推定できます。たとえば、Schiller と Naumann のモデルによると、
では、球状粒子にとって粘性効果と慣性効果の両方が重要です。したがって、ドラッグ係数は相対的 Reynolds 数の複雑な関数であり、これは Morsi と Alexander のモデルまたはその他の相関によって推定できます。たとえば、Schiller と Naumann のモデルによると、参照: L. Schiller and Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
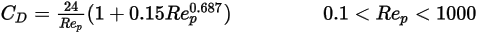
式 2.377
式 2.370で抵抗力の項の式を簡略化するために、微粒子緩和時間 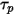 が使用されています。
が使用されています。
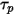 が使用されています。
が使用されています。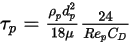
式 2.378
式 2.368、式 2.371、式 2.372、式 2.373、および式 2.378を組み合わせると、単位粒子質量あたりの抵抗力の式は次のようになります。
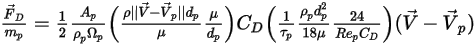
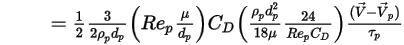
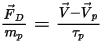
式 2.379
したがって、デフォルトの (抵抗力のみが考慮される) 粒子のフォースバランスの式は、次のように表されます。
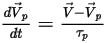
式 2.380
• 重力の項の追加
デフォルトでは、重力の項は粒子のフォースバランスの式に含められません。Creo Flow Analysis では、重力の項をアクティブ化できます。流体流れに浸された粒子の場合、重力の影響により、粒子が変位させた流体の重量に等しい浮力が生じます。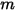 は粒子が変位させた流体質量で、
は粒子が変位させた流体質量で、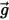 は重力ベクトルであるとすると、フォースは次のようになります。
は重力ベクトルであるとすると、フォースは次のようになります。
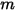 は粒子が変位させた流体質量で、
は粒子が変位させた流体質量で、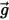 は重力ベクトルであるとすると、フォースは次のようになります。
は重力ベクトルであるとすると、フォースは次のようになります。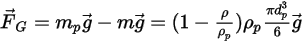
式 2.381
または、単位粒子質量あたりのフォースは次のようになります。
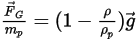
式 2.382
フォースバランスの式の形式は次のとおりです。
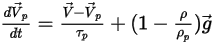
式 2.383
• 粒子上の回転力
回転参照フレーム内のモデルの流体フローの場合、回転によって発生する追加のフォースの項 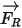 は、粒子加速度の本質的な部分の 1 つです。これは、コリオリの効果と求心力で構成されています。
は、粒子加速度の本質的な部分の 1 つです。これは、コリオリの効果と求心力で構成されています。
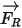 は、粒子加速度の本質的な部分の 1 つです。これは、コリオリの効果と求心力で構成されています。
は、粒子加速度の本質的な部分の 1 つです。これは、コリオリの効果と求心力で構成されています。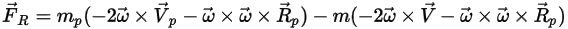
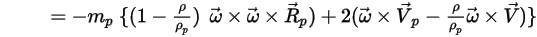
式 2.384
または、単位粒子質量あたりの回転力は次のようになります。
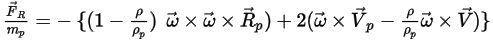
式 2.385
ここで、
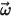 | 回転参照フレームの角速度 |
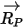 | 軸心と粒子の位置を接続するベクトル |
このフォースの項の追加により、粒子のバランスの式は次のようになります。
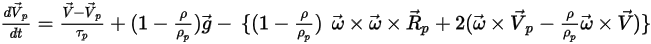
式 2.386
式 2.386は、流れが回転参照フレームで計算されるときのラグランジュ系での粒子の運動を制御します。
粒子の境界条件と初期条件
ラグランジュ的手法では、粒子の追跡は非定常プロセスです。したがって、粒子の軌道を計算するには、境界条件と初期条件が必要です。境界条件は、計算ドメインの境界での粒子の反力を定義します (特に粒子-ウォール相互作用)。初期条件は、境界からの粒子のリリースについて決定し、これにはリリース位置、頻度、速度、粒子のタイプとサイズ (半径)、粒子の数などがあります。
境界条件
Creo Flow Analysis には、境界での粒子の反力を決定する離散相境界条件が用意されています。粒子がウォールや入口境界などの流れドメインの境界 (物理的な境界と固体-流体インタフェースを含む) に到達すると、以下のいずれかが発生します。
• 粒子は弾性衝突または非弾性衝突によって反射する。
• 粒子は境界を通って脱出し、境界との衝突点での計算から失われる。
• 粒子はウォールで捕捉され、境界との衝突点での計算から失われる。
• 粒子はファンや多孔ジャンプなどの内側境界ゾーンを通る。
• ユーザー定義の、粒子が境界に衝突したときの粒子の反力をモデル化する方法によって粒子-境界相互作用が決定される。
流れ境界条件とインタフェースは、境界での粒子の反力に基づいて、オープン、対称、およびウォールの 3 つのタイプの離散粒子境界条件に再グループ化されます。
• オープン離散粒子境界
粒子または流線は、計算ドメインを出ることができます。オープン境界は、オイラー系の流体流れ相の入口または出口境界です。これは、ウォールや対称などの流れ境界についても同じです。オープン粒子境界では、粒子は粒子速度の方向に応じてドメインを出入りします。
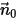 を、粒子境界速度が
を、粒子境界速度が 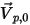 の、計算ドメインから離れる方向を指すオープン境界への単位法線ベクトルとします。
の、計算ドメインから離れる方向を指すオープン境界への単位法線ベクトルとします。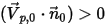 の場合、速度ベクトル
の場合、速度ベクトル 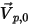 は、計算ドメインから離れる方向を指します。これは、粒子が境界を通って脱出し、境界との衝突点での計算から失われることを示します。
は、計算ドメインから離れる方向を指します。これは、粒子が境界を通って脱出し、境界との衝突点での計算から失われることを示します。• 対称粒子境界
計算ドメイン内の粒子または流線が離散対称境界に衝突すると、それは境界条件によってドメインに反射します。離散粒子相の場合、通常、対称粒子境界はオイラー系の流れ対称に対応します。これは、粒子のリリースの位置についても同じです。
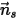 を、対称から離れて計算ドメインに向かう方向の、対称の点
を、対称から離れて計算ドメインに向かう方向の、対称の点 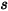 での法線-対称単位ベクトルとします。
での法線-対称単位ベクトルとします。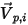 と
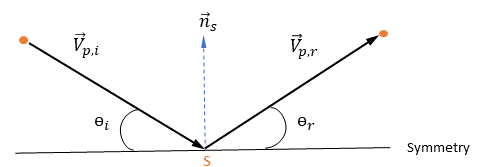
と 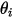 は、次の図に示すように、粒子対称境界での粒子のインパクト速度の角度を示します。粒子が対称から反射するとき、その運動エネルギーが完全に節約されます。接線速度は同じままで、法線速度は成分の記号のみが変わります。粒子対称境界条件は次のように表されます。
は、次の図に示すように、粒子対称境界での粒子のインパクト速度の角度を示します。粒子が対称から反射するとき、その運動エネルギーが完全に節約されます。接線速度は同じままで、法線速度は成分の記号のみが変わります。粒子対称境界条件は次のように表されます。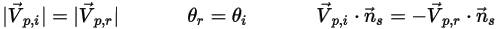
式 2.387
ここで、
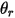 | 対称の点 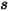 : での角度 (度) : での角度 (度) |
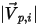 | 粒子の入射速度のマグニチュード (m/s) |
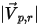 | 粒子の反射速度のマグニチュード (m/s) |
• ウォール粒子境界
液滴の場合、滴-ウォール相互作用は、ウォールの温度、ウォールの材料と粗さ、衝突角度とインパクト速度、ウォール膜の存在、およびその他のさまざまなパラメータによって異なります。したがって、さまざまなウォール-粒子相互作用の方式を再現し、流れパラメータとウォール境界条件の影響を考慮するために、さまざまなサブモデルが使用されます。
現在の離散粒子モデルでは、粒子の形状、サイズ、および質量は変更されないものと推定します。また、流体と粒子は熱平衡状態であると見なします。したがって、粒子 (質量あり) がウォールに干渉するプロセスは、単純なアプローチで説明されます。干渉プロセス中、粒子はウォールとのみ運動量を交換し、粒子は 3 つの方法のいずれかでウォールと相互作用します。これら 3 つの方法は、完全反射、付着反射、および部分反射です。
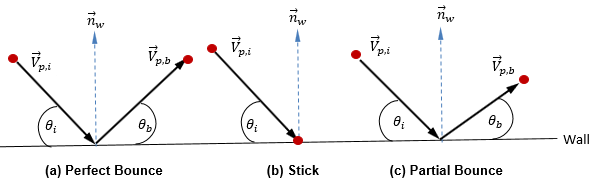
◦ 完全反射 - 粒子または流線は、ウォールに衝突するときに反射します。粒子の運動量と運動エネルギーは完全に節約されます。入射の角度は反射の角度に等しく、ウォールの法線速度は成分の記号が変わります。
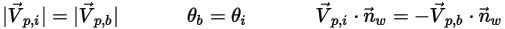
式 2.388
ここで、
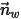 | ウォールの法線単位ベクトル |
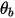 | ウォール境界での角度 (度) |
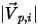 | 粒子の入射速度のマグニチュード (m/s) |
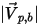 | 粒子の反射速度のマグニチュード (m/s) |
◦ 付着 - 粒子はウォールに衝突し、そのすべての運動量とエネルギーを失い、ウォールに付着します。
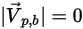
ウォールに沿った粒子の蓄積が考慮されないため、粒子は境界との衝突点での計算から完全に失われます。
◦ 部分反射 - このウォール粒子条件は、完全反射と付着の間に相当します。粒子または流線はウォールから反射しますが、法線、接線、または法線と接線の両方の方向のエネルギーを部分的に失います。粒子の運動量と運動エネルギーは節約されず、一般的に入射の角度は反射の角度よりも大きくなります。
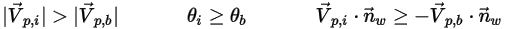
粒子-ウォール相互作用によるエネルギーの損失は、ユーザー入力によって指定されます。
▪ 法線方向のエネルギー損失 - ウォールにおける粒子の運動エネルギーの法線方向の成分の損失を指定します。
▪ 接線方向のエネルギー損失 - ウォールにおける粒子の運動エネルギーの接線方向の成分の損失を指定します。
Creo Flow Analysis では、粒子が反射するかどうか、または付着するかどうかは、指定した最大法線速度と最小法線速度の値によって決定されます。指定した粒子の最大法線速度が 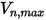 、最小法線速度が
、最小法線速度が 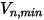 であるとすると、条件は以下のようになります。
であるとすると、条件は以下のようになります。
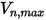 、最小法線速度が
、最小法線速度が 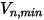 であるとすると、条件は以下のようになります。
であるとすると、条件は以下のようになります。▪ 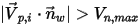 または
または 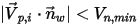 の場合、粒子はウォールから反射します。
の場合、粒子はウォールから反射します。
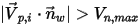 または
または 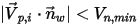 の場合、粒子はウォールから反射します。
の場合、粒子はウォールから反射します。▪ 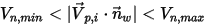 の場合、粒子はウォールに付着します。
の場合、粒子はウォールに付着します。
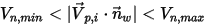 の場合、粒子はウォールに付着します。
の場合、粒子はウォールに付着します。粒子-ウォール相互作用モデルは、「質量あり」(Has Mass) に設定されている粒子にのみ適用されます。質量のない粒子は、ウォールに沿った流れ流線に従います。
粒子ウォール境界は外部ウォールであったり流体-固体インタフェースであったりすることに注意してください。オープンおよび対称粒子境界と同様に、粒子はウォール境界からリリースできます。
初期条件 (粒子をリリース)
初期条件は、個々の粒子の瞬間状態を記述するすべての依存離散相変数の開始値を指定します。ラグランジュ系の粒子の追跡の場合、初期条件の決定の手順において、境界 (オープン、対称、ウォール、およびインタフェース) からの粒子のリリース (頻度と分布) と、各粒子への特性の指定が行われます。
「粒子をリリース」(Release Particle) をアクティブ化すると、以下のパラメータまたは変数が粒子の運動の初期条件になります。
粒子の運動方程式の積分
粒子の運動を追跡するために、各粒子の軌道方程式がラグランジュ系で解析的または数値的に計算 (積分) されます。式 2.367と式 2.386から、運動方程式は次のように書き換えられます。
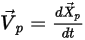
式 2.391
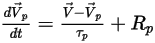
式 2.392
ここで、
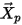 | 粒子の位置ベクトル |
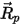 | 抵抗力を除くすべてのフォース (重力、回転効果など) を原因とする加速度を含める |
式 2.391と方程式 2.392は、1 組の結合された常微分方程式です。指定された初期条件と境界条件に基づき、粒子の変位式 2.391は、時間ステップ 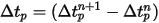 にわたる粒子速度の前方オイラー積分を使用して計算されます。
にわたる粒子速度の前方オイラー積分を使用して計算されます。
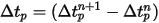 にわたる粒子速度の前方オイラー積分を使用して計算されます。
にわたる粒子速度の前方オイラー積分を使用して計算されます。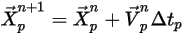
式 2.393
ここで、
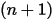 | 新しい値 |
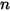 | 現在の値 |
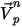 | 現在の時間ステップでの粒子速度 |
最初の時間ステップでは、
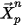 | リリース位置 |
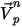 | 初期速度 |
ここで、

式 2.394
この前方積分方法では、時間ステップの開始時に計算された粒子速度がステップ全体よりも優先されるものと推定されます。時間ステップの終了時に、粒子の運動量式 2.392を解くことによって、新しい粒子速度が計算されます。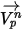 、
、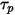 、および
、および 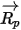 が期間
が期間 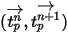 にわたって一定であり、流体の特性が時間
にわたって一定であり、流体の特性が時間 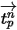 で時間ステップの開始から取得されるとすると、式 2.392の解析的な解は次のようになります。
で時間ステップの開始から取得されるとすると、式 2.392の解析的な解は次のようになります。
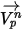 、
、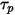 、および
、および 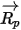 が期間
が期間 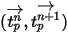 にわたって一定であり、流体の特性が時間
にわたって一定であり、流体の特性が時間 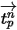 で時間ステップの開始から取得されるとすると、式 2.392の解析的な解は次のようになります。
で時間ステップの開始から取得されるとすると、式 2.392の解析的な解は次のようになります。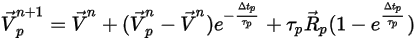
式 2.395
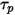 と
と 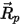 を評価するには、粒子の位置における密度、粘度、速度などの流体変数が必要です。これらは、粒子が現在位置する流体流れ相のセル値と見なされます。この解析スキームは効率的ですが、時間ステップが大きい場合、および粒子が連続流体流れと流体力学的に平衡ではない状況においては、正確ではない可能性があります。このような場合、数値スキームで式 2.392を積分します。
を評価するには、粒子の位置における密度、粘度、速度などの流体変数が必要です。これらは、粒子が現在位置する流体流れ相のセル値と見なされます。この解析スキームは効率的ですが、時間ステップが大きい場合、および粒子が連続流体流れと流体力学的に平衡ではない状況においては、正確ではない可能性があります。このような場合、数値スキームで式 2.392を積分します。粒子-流体結合
オイラー-ラグランジュ的手法では、連続流体流れはフォース、熱、および質量移動によって粒子の反力に影響を与えるものと推定されます。たとえば、粒子のフォースバランス式 2.370内のフォースの項 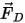 は、粒子上の流れの流線型抵抗力を表します。粒子相は離散と見なされ、ボリューム内の流体を変位させませんが、粒子は、運動量、および場合によっては質量と熱の交換によって、流体流れに反作用力の影響を与える可能性があります。この流れに対する粒子の影響を、粒子-流体結合と呼びます。これには 2 つのカテゴリがあります。
は、粒子上の流れの流線型抵抗力を表します。粒子相は離散と見なされ、ボリューム内の流体を変位させませんが、粒子は、運動量、および場合によっては質量と熱の交換によって、流体流れに反作用力の影響を与える可能性があります。この流れに対する粒子の影響を、粒子-流体結合と呼びます。これには 2 つのカテゴリがあります。
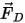 は、粒子上の流れの流線型抵抗力を表します。粒子相は離散と見なされ、ボリューム内の流体を変位させませんが、粒子は、運動量、および場合によっては質量と熱の交換によって、流体流れに反作用力の影響を与える可能性があります。この流れに対する粒子の影響を、粒子-流体結合と呼びます。これには 2 つのカテゴリがあります。
は、粒子上の流れの流線型抵抗力を表します。粒子相は離散と見なされ、ボリューム内の流体を変位させませんが、粒子は、運動量、および場合によっては質量と熱の交換によって、流体流れに反作用力の影響を与える可能性があります。この流れに対する粒子の影響を、粒子-流体結合と呼びます。これには 2 つのカテゴリがあります。• 一方向結合
一方向結合では、流体は粒子の軌道に影響を与えることができますが、粒子は流体に影響を与えません。質量のない粒子の場合、粒子-流体相互作用は一方向結合で、粒子は流体流れとともに移動します。質量がある粒子の場合、一方向結合は、粒子の流体流れに対する影響がごくわずかな分散相の荷重が低い流れにおいては、許容できる近似である場合があります。
連続流体相の場合、流れフィールドは、分散粒子相が存在しない単相流体流れとして計算されます。これにより、流体の運動は、計算された流れ場と初期条件に基づいて追跡されます。定常流れの場合、粒子の追跡は、連続方程式とナビエ-ストークス方程式を解くことによって収束した流れの解が取得された後に発生します。非定常流れシミュレーションの場合、粒子の運動は、流れシミュレーションの各時間ステップの終了時に追跡されます。
• 双方向結合
質量がある粒子の場合、双方向結合では、流体は粒子の軌道に影響を与えることができます。これは、連続流体相に対する粒子の影響も考慮します。質量と熱伝達を含めない場合、流体と粒子の間の双方向の相互作用は、運動量の交換のみを表します。連続相から離散相に伝達された運動量は、個々の粒子が制御ボリュームを通るときに得た運動量または失った運動量を追跡することによって計算されます。双方向結合では、連続体に対する離散相の軌道の影響を考慮するために、流体運動量方程式に粒子-流体運動量交換を含めなければなりません。式 2.386からは、抵抗力のみが粒子-流体運動量交換を考慮し、運動量方程式に追加されます。質量のない粒子の場合、流体流れとの交換の項は計算されないため、離散相の軌道は連続体に影響を与えないことに注意してください。
連続相の運動量方程式に粒子-流体抗力効果を含めるために、流れを移動する各粒子の抵抗力が、時間ステップ中に粒子が位置する制御ボリュームで適用されます。粒子 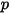 については、抵抗
については、抵抗 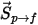 を原因とするその運動量ソースを次の微分方程式から計算します。
を原因とするその運動量ソースを次の微分方程式から計算します。
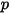 については、抵抗
については、抵抗 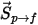 を原因とするその運動量ソースを次の微分方程式から計算します。
を原因とするその運動量ソースを次の微分方程式から計算します。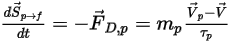
式 2.396
連続相への粒子ソースは、その粒子の数値流速 (粒子の質量で割った質量流速) を掛け合わせたソース項 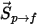 です。
です。
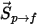 です。
です。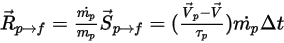
式 2.397
ここで、
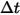 | 時間ステップ |
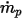 | 粒子の質量流量 |
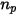 は時間ステップ
は時間ステップ 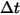 で制御ボリュームを通る粒子の数であるとすると、合計粒子-流体ソース項は次のようになります。
で制御ボリュームを通る粒子の数であるとすると、合計粒子-流体ソース項は次のようになります。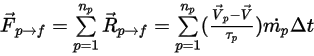
式 2.398
流体-粒子抵抗力の追加により、連続相について計算された支配方程式は次のように表されます。
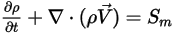
式 2.399
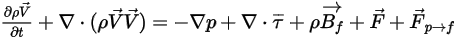
式 2.400
一方向結合 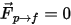 を使用する場合、連続流体相は正確な単相連続方程式および運動量方程式によって支配されます。双方向結合の場合、追加の粒子-流体抵抗力ソース項があります。式 2.399と方程式 2.400の計算は、単相流れと同一です。
を使用する場合、連続流体相は正確な単相連続方程式および運動量方程式によって支配されます。双方向結合の場合、追加の粒子-流体抵抗力ソース項があります。式 2.399と方程式 2.400の計算は、単相流れと同一です。
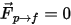 を使用する場合、連続流体相は正確な単相連続方程式および運動量方程式によって支配されます。双方向結合の場合、追加の粒子-流体抵抗力ソース項があります。式 2.399と方程式 2.400の計算は、単相流れと同一です。
を使用する場合、連続流体相は正確な単相連続方程式および運動量方程式によって支配されます。双方向結合の場合、追加の粒子-流体抵抗力ソース項があります。式 2.399と方程式 2.400の計算は、単相流れと同一です。