Solutore ODE
L'equazione 2.432 e l'equazione 2.444, che sono le equazioni differenziali ordinarie (ODE) che regolano rispettivamente la traslazione e la rotazione a 1 grado di libertà dei limiti e dei volumi, vengono risolte numericamente in Creo Flow Analysis. In particolare, per calcolare il movimento e lo spostamento di un limite e di un volume per l'esecuzione di remesh, per integrare le equazioni differenziali ordinarie vengono adottati i seguenti schemi di marcia temporale: solutore esplicito di Runge-Kutta, di Eulero e per differenziali stiff.
Integrazione dell'equazione della traslazione a un grado di libertà
Sostituendo l'equazione 2.434, l'equazione 2.435 e l'equazione 2.436 nell'equazione 2.432 e raggruppando i termini di forza espliciti in un singolo termine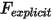 
per brevità, l'equazione della traslazione a 1 grado di libertà del movimento viene riscritta nella forma seguente:
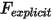per brevità, l'equazione della traslazione a 1 grado di libertà del movimento viene riscritta nella forma seguente: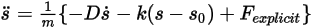
Equazione 2.455
dove il termine di forza calcolato in modo esplicito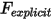 
è:
è:
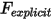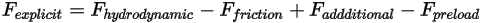
Equazione 2.456
Con le condizioni iniziali e al limite specificate, lo spostamento del corpo solido viene ottenuto integrando l'equazione 2.455 con schemi di marcia temporale espliciti. Nel passo temporale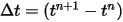 
, le formule generali sono le seguenti:
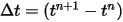, le formule generali sono le seguenti: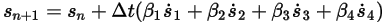
Equazione 2.457
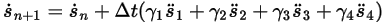
Equazione 2.458
dove la somma dei fattori di peso è l'unità:
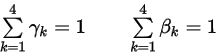
Equazione 2.459
Con la scelta dei fattori di peso vengono derivati diversi schemi. Di seguito sono riportati ad esempio gli schemi espliciti di Eulero e di Runge-Kutta.
• Solutore esplicito di Eulero (primo ordine)
Con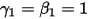 
e 
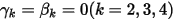, lo schema esplicito di Eulero è il seguent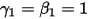e:
e 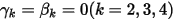, lo schema esplicito di Eulero è il seguente: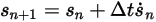
Equazione 2.460
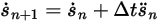
Equazione 2.461
• Solutore esplicito di Runge-Kutta
I solutori di Runge-Kutta sono schemi espliciti del 2° e del 4° ordine, riportati di seguito.
◦ Schema del secondo ordine
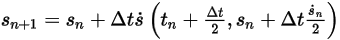
Equazione 2.462
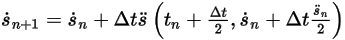
Equazione 2.463
◦ Schema del quarto ordine
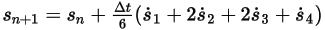
Equazione 2.464
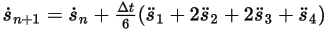
Equazione 2.465
dove
Equazione 2.466
Equazione 2.467
Equazione 2.468
Equazione 2.469
• Solutore per differenziali stiff (esplicito)
In aggiunta agli schemi standard di Eulero e di Runge-Kutta, in Creo Flow Analysis è stato sviluppato un solutore per differenziali stiff per integrare l'equazione differenziale ordinaria della traslazione a 1 grado di libertà. È il metodo di default per i movimenti dinamici dei corpi solidi.
Integrazione dell'equazione della rotazione a un grado di libertà
Come per la traslazione, sostituendo l'equazione 2.446 e l'equazione 2.447 nell'equazione 2.444 e raggruppando i termini di coppia espliciti in un singolo termine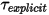 
per brevità, l'equazione della rotazione a 1 grado di libertà del movimento (equazione 2.444) viene riscritta nella forma seguente:
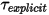per brevità, l'equazione della rotazione a 1 grado di libertà del movimento (equazione 2.444) viene riscritta nella forma seguente: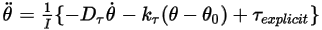
Equazione 2.470
dove il termine di coppia calcolato in modo esplicito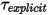 
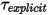è:
è: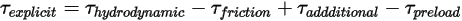
Equazione 2.471
Con le condizioni iniziali e al limite specificate, l'angolo di rotazione viene ottenuto integrando l'equazione 2.470 con schemi di marcia temporale espliciti. Nel passo temporale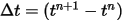 
, le formule generali sono le seguenti:
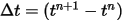, le formule generali sono le seguenti: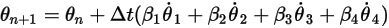
Equazione 2.472
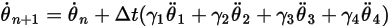
Equazione 2.473
dove la somma dei fattori di peso è l'unità:
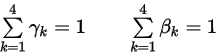
Equazione 2.474
Con la scelta dei fattori di peso vengono facilmente derivati diversi schemi. Di seguito sono riportati gli schemi espliciti di Eulero e di Runge-Kutta.
• Solutore esplicito di Eulero (primo ordine)
Con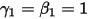 
e 
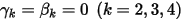, lo schema esplicito di Eulero è il seguent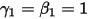e:
e 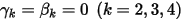, lo schema esplicito di Eulero è il seguente: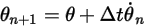
Equazione 2.475
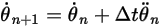
Equazione 2.476
• Solutore esplicito di Runge-Kutta
I solutori di Runge-Kutta sono schemi espliciti del 2° e del 4° ordine, riportati di seguito.
◦ Schema del secondo ordine
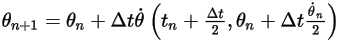
Equazione 2.477
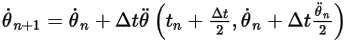
Equazione 2.478
◦ Schema del quarto ordine
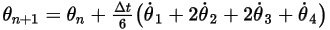
Equazione 2.479
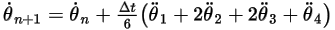
Equazione 2.480
dove
Equazione 2.481
Equazione 2.482
Equazione 2.483
Equazione 2.484
• Solutore per differenziali stiff (esplicito)
In aggiunta agli schemi standard di Eulero e di Runge-Kutta, in Creo Flow Analysis è stato sviluppato un solutore per differenziali stiff per integrare l'equazione differenziale ordinaria della rotazione a 1 grado di libertà (equazione 2.444). È il metodo di default per i movimenti dinamici dei corpi solidi.