Gleichungen für Schaleneigenschaften
Dieses Dokument beschreibt die mathematische Darstellung strukturmechanischer Schaleneigenschaften in Creo Simulate. Außerdem finden Sie hier eine Liste der Terminologie, die in Creo Simulate zur Beschreibung der Schaleneigenschaften und Schalenergebnisse verwendet wird.
Das Dokument ist in folgende Abschnitte unterteilt:
Thema
Übersicht
Die in diesem Dokument beschriebenen Formeln drücken die grundlegenden Beziehungen zwischen Schalenkräften, Momenten, Dehnungen, Krümmungsänderungen, Schaleneigenschaften und Schalenergebnissen aus. Die Formeln stellen eine eindeutige Definition der Konventionen bereit, anhand derer die verschiedenen Modell- und Ergebnisdaten für Schalen beschrieben werden.
Im Dialogfenster Schaleneigenschaften definieren (Shell Property Definition) geben Sie Eigenschaften für die Laminatsteifigkeit an, die das mechanische Verhalten laminierter Schalen bestimmen. Weitere Informationen finden Sie unter Schaleneigenschaften. An dem Punkt, für den Sie sich Ergebnisse anzeigen lassen möchten, definieren Sie bezüglich der Materialorientierung die folgenden Eigenschaften:
• Schalendehnsteifigkeiten
• Schalenquerschubsteifigkeiten
• Schalendehnbiegungs-Kopplungssteifigkeiten
• Schalenbiegungssteifigkeiten
• Wärmemomentkoeffizienten der Schalenresultierenden
• Wärmekraftkoeffizient der Schalenresultierenden
• Masse pro Flächeneinheit
• Rotationsträgheit pro Flächeneinheit
Sie können die folgenden resultierenden Mengen bezüglich der Materialorientierung an wichtigen Punkten oder in Bezug auf ein Koordinatensystem überprüfen. Weitere Informationen finden Sie unter Relative Ergebnisse.
• Rotation der Schalenmittenfläche um die x- und y-Achse
• Mittenflächendehnung
• Krümmungsänderung der Schalenmittenfläche
• Moment der Schalenresultierenden
• Kraft der Schalenresultierenden
• Schalenquerschubkraft
• Spannung
• Verschiebung der Schalenmittenfläche
Die Symbole für diese Ausdrücke finden Sie in der Symbolliste.
Diese Formeln und Beschreibungen stellen kein Tutorial für die Analyse von Schalen dar. Detaillierte Informationen über die Modellierung laminierter oder orthotroper Schalen finden Sie in Texten von Jones (1), Reddy (2), Tsai (3) Ugural (4) und anderen. Weitere Hinweise auf diese Texte finden Sie in der Bibliographie.
Die Abbildungen und Gleichungen in diesem Abschnitt beziehen sich auf flache Schalen oder Platten. Die hier dargestellten maschinenbaulichen Konzepte verallgemeinern zu gekrümmten Schalen. Da die mathematische Beschreibung gekrümmter Schalen jedoch sehr kompliziert ist, wird an dieser Stelle darauf verzichtet.
Formel für die Berechnung von Schaleneigenschaften
Eine Schale ist ein Teilstück eines Creo Simulate Modells, das sehr dünn, zugleich aber lang und breit ist. Aus Gründen der effizienteren Berechnung empfiehlt es sich, dünne Bereiche einer Struktur als Schalen zu modellieren. Die Effizienz gründet sich zum Teil auf allgemeine Annahmen über das Verhalten von Schalen. In anderen Worten: Das mechanische Verhalten einer Schale lässt sich näherungsweise durch eine Beschreibung des mechanischen Verhaltens ihrer Mittenfläche ausdrücken.
Es ist also möglich, die Verschiebung einer Schale über die Rotation und Verschiebung ihrer Mittenfläche, die Dehnung einer Schale über die Dehnung und Krümmungsänderung ihrer Mittenfläche und das Gleichgewicht einer Schale über das Gleichgewicht der Spannungen zu beschreiben, die sich aus der Dicke der Schale ergeben.
Die folgende Abbildung zeigt eine flache rechteckige Schale, deren Kanten an der x- und y-Achse eines kartesischen Koordinatensystems ausgerichtet sind. Die XY-Ebene dieses Koordinatensystems befindet sich in der Mitte zwischen der oberen und der unteren Fläche der Schale; daher liegt die Mittenfläche der Schale bei z=0. Da die Schale die Dicke t aufweist, liegt die obere Fläche bei z = t/2 und die untere Fläche bei z = -t/2, wie die folgende Abbildung zeigt:
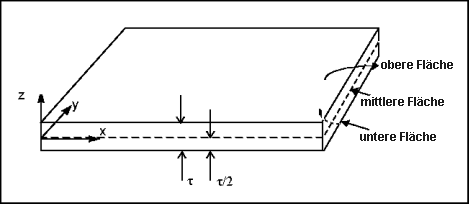
Wie bereits erwähnt gilt die Annahme, dass die Verschiebung eines beliebigen Punktes (x, y, z) innerhalb der Schale als Verschiebung und Rotation des Punktes (x, y, 0) auf der Mittenfläche der Schale ausgedrückt werden kann. Speziell gilt die Annahme, dass:
Dabei gilt:
• 
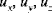sind die Komponenten der Verschiebung in x-, y- bzw. z-Richtung
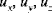sind die Komponenten der Verschiebung in x-, y- bzw. z-Richtung• 
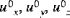sind die Komponenten der Verschiebung der Mittenfläche
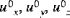sind die Komponenten der Verschiebung der Mittenfläche• 
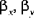sind die (geringfügigen) Rotationen der Mittenfläche um die x- bzw. y-Achse
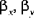sind die (geringfügigen) Rotationen der Mittenfläche um die x- bzw. y-AchseIn ähnlicher Weise können die Dehnungskomponenten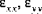 
und 
eines beliebigen Punktes (x,y,z) wie folgt als Dehnungen (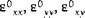
) und Krümmungsänderungen (
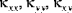) der Mittenfläche (oder Membran) ausgedrückt werden:
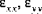und eines beliebigen Punktes (x,y,z) wie folgt als Dehnungen (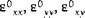) und Krümmungsänderungen (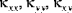) der Mittenfläche (oder Membran) ausgedrückt werden: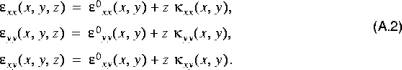
Beachten Sie, dass die Gleichung (A.2) die Schubdehnungskomponenten des Tensors (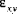
und 
) und 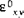nicht die maschinenbaulichen Schubdehnungskomponenten enthält, deren Werte doppelt so hoch sind wie die Werte des Tensors.
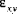und 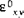) und nicht die maschinenbaulichen Schubdehnungskomponenten enthält, deren Werte doppelt so hoch sind wie die Werte des Tensors.Für flache Schalen gelten folgende Tensor-Schubdehnungskomponenten:
und
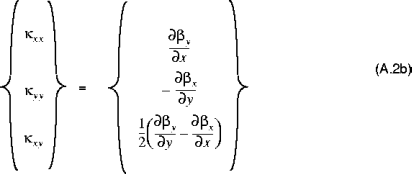
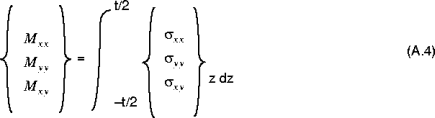
Die Kräfte der Schalenresultierenden (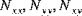
), die Momente der Schalenresultierenden (
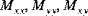) und die Schalenquerschubkräfte (
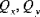) werden ermittelt, indem die Spannungskomponenten 
über die Dicke der Schale einbezogen werden. Die Kräfte der Schalenresultierenden sind gegeben durch:
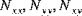), die Momente der Schalenresultierenden (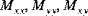) und die Schalenquerschubkräfte (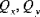) werden ermittelt, indem die Spannungskomponenten über die Dicke der Schale einbezogen werden. Die Kräfte der Schalenresultierenden sind gegeben durch:
Die Momente der Schalenresultierenden sind gegeben durch:
Die Schalenquerschubkräfte sind gegeben durch:
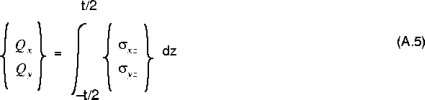
Die folgende Abbildung zeigt die Vorzeichenkonventionen, die in Mechanica für resultierende Kräfte, resultierende Momente und Querschubkräfte verwendet werden. Beachten Sie, dass ein positives Moment (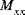
) in der oberen Schalenhälfte (z > 0) eine positive Dehnung (
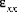), in der unteren Schalenhälfte (z < 0) dagegen eine negative Dehnung bewirkt.
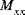) in der oberen Schalenhälfte (z > 0) eine positive Dehnung (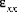), in der unteren Schalenhälfte (z < 0) dagegen eine negative Dehnung bewirkt.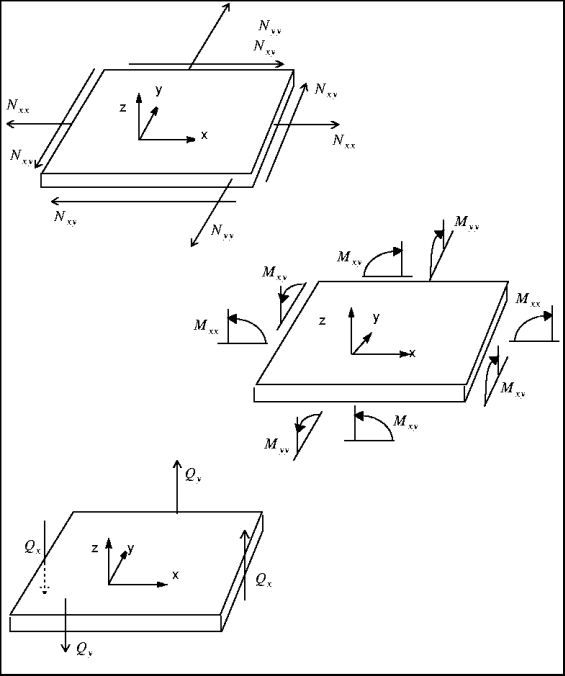
Die Beziehungen zwischen den Schalenresultierenden und den Dehnungen und Krümmungsänderungen der Mittenfläche sind gegeben durch:
und
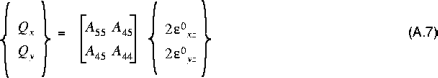
In Gleichung (A.6) werden die Größen 
(wobei i,j = 1,2,6) als Dehnsteifigkeiten, die Größen 
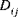als Biegesteifigkeiten, die Größen 
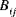als Dehnbiegungs-Kopplungssteifigkeiten und die Größen 
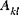(wobei k,l = 4,5) als Querschubsteifigkeiten bezeichnet. Die Größen 
und 
sind die Querschubdehnungen auf der Mittenfläche. Die Größen 
und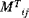 
sind die resultierenden Wärmekräfte bzw. -momente.
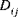(wobei i,j = 1,2,6) als Dehnsteifigkeiten, die Größen als Biegesteifigkeiten, die Größen 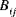als Dehnbiegungs-Kopplungssteifigkeiten und die Größen 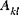(wobei k,l = 4,5) als Querschubsteifigkeiten bezeichnet. Die Größen und sind die Querschubdehnungen auf der Mittenfläche. Die Größen und 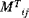sind die resultierenden Wärmekräfte bzw. -momente.Die in den Gleichungen (A.6) und (A.7) eingeführten Schalensteifigkeiten und Wärmeresultierenden sind durch Einbinden der Materialeigenschaften der Schale über die Dicke der Schale definiert. Die Dehnsteifigkeit, die Biegesteifigkeit und die Dehnbiegungssteifigkeit sind gegeben durch:
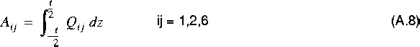und: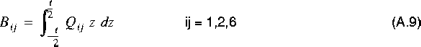
und
Dabei sind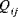 
die reduzierten Steifigkeiten des Materials.
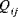die reduzierten Steifigkeiten des Materials.Die Querschubsteifigkeit ist gegeben durch:
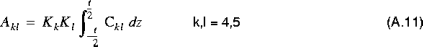
Dabei gilt:
• 
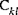sind die (nicht reduzierten) Steifigkeiten des Materials, und
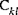sind die (nicht reduzierten) Steifigkeiten des Materials, und• 
sind die Koeffizienten der Schubkorrektur, die bei homogenen Schalen oft als 
angenommen werden.
sind die Koeffizienten der Schubkorrektur, die bei homogenen Schalen oft als angenommen werden.Beachten Sie, dass das Integral in Gleichung (A.9) verschwindet und die Dehnbiegungs-Kopplungssteifigkeiten 
gleich Null sind, wenn das Material der Schale symmetrisch über die Mittenfläche verteilt ist.
gleich Null sind, wenn das Material der Schale symmetrisch über die Mittenfläche verteilt ist.Die resultierenden Wärmekräfte und -momente sind gegeben durch:
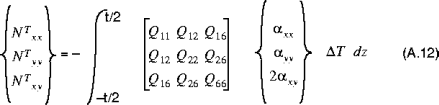
und
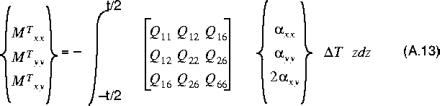
Dabei gilt:
• 
sind die Wärmeausdehnungskoeffizienten des Materials, und
sind die Wärmeausdehnungskoeffizienten des Materials, und• 
ist die Temperaturänderung gegenüber dem spannungsfreien Zustand.
ist die Temperaturänderung gegenüber dem spannungsfreien Zustand.Verläuft die Temperaturänderung gleichmäßig durch die gesamte Dicke der Schale, können die Größen 
aus den Gleichungen (A.12) und (A.13) entfernt werden. Es ergeben sich die Gleichungen (A.14) und (A.15):
aus den Gleichungen (A.12) und (A.13) entfernt werden. Es ergeben sich die Gleichungen (A.14) und (A.15):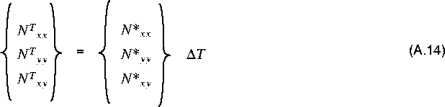
bezeichnet man als Wärmekoeffizienten der Schalenresultierenden. Sie sind gegeben durch:
Auch die Masseneigenschaften für Schalen werden durch Einbinden der Materialeigenschaftsdaten über die Dicke der Schale ermittelt. Die Masse pro Flächeneinheit (
) ist gegeben durch:
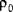) ist gegeben durch:
Dabei ist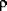 
die Dichte des Materials.
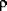die Dichte des Materials.Die Rotationsträgheit pro Flächeneinheit (
) ist gegeben durch:
) ist gegeben durch:
Liste der Symbole
Die folgende Tabelle enthält die Symbole, die in diesem Dokument verwendet werden.
Symbol | Definition |
|---|---|
 | Wärmeausdehnungskoeffizienten |
 (i,j = 1,2,6) | Schalendehnsteifigkeit |
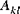 (k,l = 4,5) | Schalenquerschubsteifigkeit |
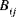 (i,j = 1,2,6) | Schalendehnbiegungs-Kopplungssteifigkeit |
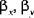 | Rotation der Schalenmittenfläche um die x- und y-Achse |
 (k,l = 4,5) | Materialsteifigkeit |
 (i,j = 1,2,6) | Schalenbiegungssteifigkeit |
 | Temperaturänderung |
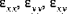 | Dehnung |
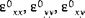 | Mittenflächendehnung (oder Membrandehnung) |
 | Krümmungsänderung der Schalenmittenfläche |
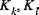 (k,l = 4,5) | Koeffizienten der Schubkorrektur |
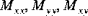 | Moment der Schalenresultierenden |
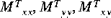 | Wärmemoment der Schalenresultierenden |
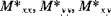 | Wärmemomentkoeffizient der Schalenresultierenden |
 | Kraft der Schalenresultierenden |
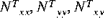 | Wärmekraft der Schalenresultierenden |
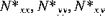 | Wärmekraftkoeffizient der Schalenresultierenden |
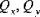 | Schalenquerschubkraft |
 (i,j = 1,2,6) | Reduzierte Materialsteifigkeit |
 | Masse pro Flächeneinheit |
 | Rotationsträgheit pro Flächeneinheit |
 | Spannung |
t | Schalendicke |
 | Verschiebung |
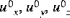 | Verschiebung der Schalenmittenfläche |
x, y | Mittenflächenkoordinaten |
z | Koordinate senkrecht zur Schalenmittenfläche |
Bibliographie
1. Jones, Robert M. Mechanics of Composite Materials. Washington, DC:Scripta Book Company, 1975.
2. Reddy, J.N. Energy and Variational Method in Applied Mechanics. New York: John Wiley & Sons, 1984.
3. Tsai, S. W. and H. T. Hahn Introduction to Composite Materials. Westport, CT: Technomic Publishing Co., 1980.
4. Ugural, A. C. Stresses in Plates and Shells. New York: McGraw-Hill Book Company, 1981.