Physique
Dans le cas d'un écoulement multicomposant, vous résolvez les équations de transport scalaires pour la vitesse du mélange, la pression, la température, la turbulence et d'autres quantités physiques. Lorsque plusieurs composants sont présents, vous devez résoudre d'autres équations afin de déterminer le mode de transport des composants dans le mélange fluide.
Description des différentes espèces (composant)
Il existe plusieurs variables différentes, mais associées pour quantifier le contenu d'un composant  dans l'écoulement
dans l'écoulement 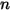 :
:
 dans l'écoulement
dans l'écoulement 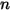 :
: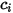 | concentration molaire du composant  |
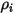 | concentration massique du composant  |
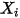 | fraction molaire du composant  |
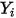 | fraction massique du composant  |
Les quatre grandeurs sont associées comme suit :
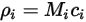
Equation 2.314
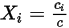
Equation 2.315
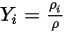
Equation 2.316
où,
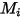 | poids moléculaire du composant  |
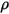 | masse volumique du mélange |
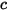 | somme des concentrations molaires de tous les composants d'un système : |
et
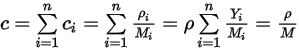
Equation 2.317
où 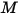 correspond au poids moléculaire du mélange :
correspond au poids moléculaire du mélange :
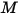 correspond au poids moléculaire du mélange :
correspond au poids moléculaire du mélange :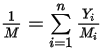
Equation 2.318
L'équation 2.317 indique qu'avec un poids moléculaire pondéré par la fraction massique du mélange, l'équation 2.314 s'applique également au mélange des composants 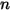 .
.
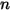 .
.En outre, dans les définitions de l'équation 2.315 et de l'équation 2.316, la somme des fractions molaire et massique doit être une unité :
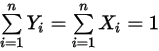
Equation 2.319
Dans les solveurs CFA, vous obtenez la fraction massique du composant arbitraire 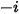 ,
, 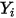 directement en résolvant des équations de transport différentielles partielles. Les autres variables (
directement en résolvant des équations de transport différentielles partielles. Les autres variables (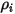 ,
, 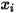 et
et 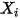 ) sont des variables auxiliaires que vous utilisez pour le post-traitement.
) sont des variables auxiliaires que vous utilisez pour le post-traitement.
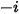 ,
, 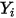 directement en résolvant des équations de transport différentielles partielles. Les autres variables (
directement en résolvant des équations de transport différentielles partielles. Les autres variables (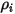 ,
, 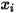 et
et 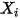 ) sont des variables auxiliaires que vous utilisez pour le post-traitement.
) sont des variables auxiliaires que vous utilisez pour le post-traitement.Equations principales
Dans un écoulement multicomposant, le mouvement global du mélange est modélisé à l'aide des champs de vitesse, de pression, de température et de turbulence. Pour le mélange et le transport des espèces chimiques, chaque composant possède sa propre équation principale de conservation de la masse. L'influence de plusieurs composants sur l'écoulement global est ressentie par la variation des propriétés de mélange, telles que la masse volumique et la viscosité, par rapport aux propriétés du composant et aux fractions massiques locales.
• Equations de fraction massique
Dans le cas de l'écoulement d'un mélange de composants  , s'il n'existe aucune réaction chimique, le transport d'un composant arbitraire
, s'il n'existe aucune réaction chimique, le transport d'un composant arbitraire  est régi par l'équation suivante :
est régi par l'équation suivante :
 , s'il n'existe aucune réaction chimique, le transport d'un composant arbitraire
, s'il n'existe aucune réaction chimique, le transport d'un composant arbitraire  est régi par l'équation suivante :
est régi par l'équation suivante :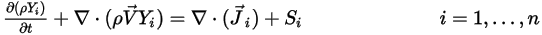
Equation 2.320
où,
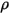 et et 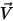 | masse volumique et vitesse du mélange |
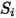 | toute source définie par l'utilisateur |
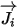 | terme de diffusion massique |
Pour les écoulements laminaires, le vecteur de vitesse 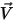 et la fraction massique
et la fraction massique 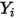 sont des variables instantanées. Pour les écoulements turbulents, ces vecteurs de vitesse sont des grandeurs moyennées de Favre, car les écoulements multicomposants sont considérés comme des écoulements compressibles ou à densité variable.
sont des variables instantanées. Pour les écoulements turbulents, ces vecteurs de vitesse sont des grandeurs moyennées de Favre, car les écoulements multicomposants sont considérés comme des écoulements compressibles ou à densité variable.
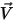 et la fraction massique
et la fraction massique 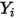 sont des variables instantanées. Pour les écoulements turbulents, ces vecteurs de vitesse sont des grandeurs moyennées de Favre, car les écoulements multicomposants sont considérés comme des écoulements compressibles ou à densité variable.
sont des variables instantanées. Pour les écoulements turbulents, ces vecteurs de vitesse sont des grandeurs moyennées de Favre, car les écoulements multicomposants sont considérés comme des écoulements compressibles ou à densité variable.Dans l'équation 2.320, les grandeurs du mélange et le terme de diffusion massique sont définis comme suit :
◦ Masse volumique du mélange : valeur massique moyenne de toutes les densités de composant :
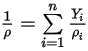
Equation 2.321
Pour un mélange d'espèces gazeuses, la masse volumique du mélange est calculée à l'aide de la loi des gaz parfaits basée sur le poids moléculaire du mélange 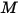 , que vous calculez à l'aide de l'équation 2.318 :
, que vous calculez à l'aide de l'équation 2.318 :
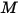 , que vous calculez à l'aide de l'équation 2.318 :
, que vous calculez à l'aide de l'équation 2.318 :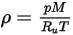
Equation 2.322
où,
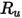 | constante universelle des gaz |
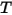 | température du mélange |
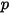 | pression absolue |
Si vous utilisez la pression de service (constante), l'équation 2.322 est réduite à la loi de gaz parfaits dite incompressible. Il s'agit d'une hypothèse appropriée pour le mélange et le transport d'espèces, où la pression manométrique est souvent négligeable par rapport à la pression de service.
◦ Vitesse du mélange : valeur massique moyenne de toutes les vitesses de composant :
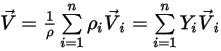
Equation 2.323
Toutefois, une seule vitesse étant résolue, vous supposez que la vitesse du mélange et toutes les vitesses de composant ont les mêmes valeurs.
◦ Flux de diffusion massique : le flux de diffusion massique du composant  est composé de deux éléments : les termes de diffusion turbulente et laminaire, qui sont exprimés comme suit :
est composé de deux éléments : les termes de diffusion turbulente et laminaire, qui sont exprimés comme suit :
 est composé de deux éléments : les termes de diffusion turbulente et laminaire, qui sont exprimés comme suit :
est composé de deux éléments : les termes de diffusion turbulente et laminaire, qui sont exprimés comme suit :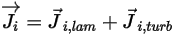
Equation 2.324
Dans l'équation 2.324, 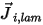 correspond au flux de diffusion laminaire du composant
correspond au flux de diffusion laminaire du composant  qui se produit suite à des gradients de concentration et de température. Par défaut, Creo Flow Analysis utilise la loi de Fick ou l'approximation diluée pour modéliser la diffusion massique due aux gradients de concentration. Le flux de diffusion laminaire présente la formule suivante :
qui se produit suite à des gradients de concentration et de température. Par défaut, Creo Flow Analysis utilise la loi de Fick ou l'approximation diluée pour modéliser la diffusion massique due aux gradients de concentration. Le flux de diffusion laminaire présente la formule suivante :
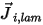 correspond au flux de diffusion laminaire du composant
correspond au flux de diffusion laminaire du composant  qui se produit suite à des gradients de concentration et de température. Par défaut, Creo Flow Analysis utilise la loi de Fick ou l'approximation diluée pour modéliser la diffusion massique due aux gradients de concentration. Le flux de diffusion laminaire présente la formule suivante :
qui se produit suite à des gradients de concentration et de température. Par défaut, Creo Flow Analysis utilise la loi de Fick ou l'approximation diluée pour modéliser la diffusion massique due aux gradients de concentration. Le flux de diffusion laminaire présente la formule suivante :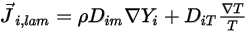
Equation 2.325
où 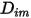 correspond au coefficient de diffusion massique du composant
correspond au coefficient de diffusion massique du composant  dans le mélange et
dans le mélange et 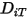 au coefficient de diffusion thermique (Soret).
au coefficient de diffusion thermique (Soret).
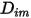 correspond au coefficient de diffusion massique du composant
correspond au coefficient de diffusion massique du composant  dans le mélange et
dans le mélange et 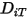 au coefficient de diffusion thermique (Soret).
au coefficient de diffusion thermique (Soret).Pour les écoulements turbulents, le terme de fluctuation dérivé de Favre moyennant l'advection dans l'équation 2.320 est modélisé comme une diffusion turbulente :
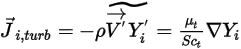
Equation 2.326
où,
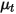 | viscosité turbulente |
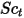 | nombre de Schmidt turbulent 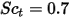 par défaut par défaut |
La diffusion turbulente l'emporte généralement sur la diffusion laminaire. La spécification des propriétés de diffusion laminaire détaillées dans les écoulements turbulents est généralement moins importante que celle de la diffusion turbulente.
Pour dériver l'équation de continuité de la masse pour le mélange de l'écoulement, ajoutez toutes les équations de fraction massique des composants et appliquez l'équation 2.319 :
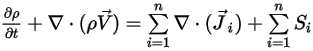
Equation 2.327
Pour remplir la condition de conservation de la masse totale du mélange de l'écoulement, la somme des termes de diffusion de tous les composants doit être égale à zéro :
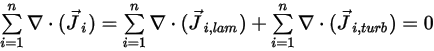
Equation 2.328
Dans l'équation 2.319 et l'équation 2.326, le terme de diffusion turbulente est toujours déterminé à zéro. Par conséquent, pour les écoulements pleinement turbulents, vous devez généralement considérer que l'équation 2.328 est automatiquement vérifiée. Toutefois, pour les écoulements laminaires, ou lorsque vous ne pouvez pas ignorer la diffusion massique laminaire dans les écoulements turbulents, l'équation 2.328 se réduit à la forme suivante :
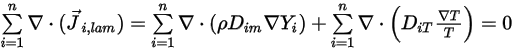
Equation 2.329
Ensuite, pour vérifier l'équation 2.329, vous appliquez les deux contraintes distinctes suivantes :
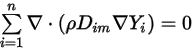
Equation 2.330
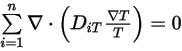
Equation 2.331
L'équation de continuité des écoulements multicomposants présente alors la forme finale suivante :
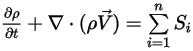
Equation 2.332
• Coefficients de diffusion
Pour résoudre l'équation 2.320 de transport pour les écoulements laminaires multicomposants, vous devez disposer du coefficient de diffusion massique 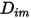 et du coefficient de diffusion thermique
et du coefficient de diffusion thermique 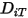 pour chaque composant d'un mélange. Les méthodes permettant de déterminer les coefficients
pour chaque composant d'un mélange. Les méthodes permettant de déterminer les coefficients 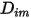 et
et 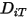 sont les suivantes :
sont les suivantes :
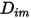 et du coefficient de diffusion thermique
et du coefficient de diffusion thermique 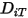 pour chaque composant d'un mélange. Les méthodes permettant de déterminer les coefficients
pour chaque composant d'un mélange. Les méthodes permettant de déterminer les coefficients 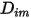 et
et 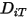 sont les suivantes :
sont les suivantes :◦ Coefficients de diffusion massique : la formule du flux de diffusion massique dans les écoulements laminaires (équation 2.325) est strictement valide lorsque la composition du mélange ne change pas ou que 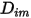 est indépendant de la composition. Il s'agit d'une approximation acceptable dans les mélanges dilués lorsque
est indépendant de la composition. Il s'agit d'une approximation acceptable dans les mélanges dilués lorsque 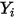 est très petit pour tous les composants, à l'exception du gaz porteur. Pour les mélanges non dilués dans les écoulements laminaires multicomposants, vous calculez
est très petit pour tous les composants, à l'exception du gaz porteur. Pour les mélanges non dilués dans les écoulements laminaires multicomposants, vous calculez 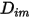 à partir de la formule suivante :
à partir de la formule suivante :
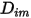 est indépendant de la composition. Il s'agit d'une approximation acceptable dans les mélanges dilués lorsque
est indépendant de la composition. Il s'agit d'une approximation acceptable dans les mélanges dilués lorsque 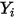 est très petit pour tous les composants, à l'exception du gaz porteur. Pour les mélanges non dilués dans les écoulements laminaires multicomposants, vous calculez
est très petit pour tous les composants, à l'exception du gaz porteur. Pour les mélanges non dilués dans les écoulements laminaires multicomposants, vous calculez 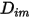 à partir de la formule suivante :
à partir de la formule suivante :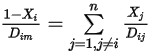
Equation 2.333
où 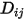 correspond au coefficient de diffusion massique binaire du composant
correspond au coefficient de diffusion massique binaire du composant  dans le composant
dans le composant 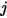 , que vous devez spécifier ou calculer.
, que vous devez spécifier ou calculer.
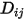 correspond au coefficient de diffusion massique binaire du composant
correspond au coefficient de diffusion massique binaire du composant  dans le composant
dans le composant 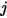 , que vous devez spécifier ou calculer.
, que vous devez spécifier ou calculer.◦ Valeur spécifiée : le coefficient de diffusion massique binaire 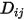 est une constante ou une fonction de température, si le transfert de chaleur est pris en compte. Vous pouvez spécifier la valeur directement ou l'obtenir à partir du nombre de Schmidt spécifié :
est une constante ou une fonction de température, si le transfert de chaleur est pris en compte. Vous pouvez spécifier la valeur directement ou l'obtenir à partir du nombre de Schmidt spécifié :
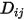 est une constante ou une fonction de température, si le transfert de chaleur est pris en compte. Vous pouvez spécifier la valeur directement ou l'obtenir à partir du nombre de Schmidt spécifié :
est une constante ou une fonction de température, si le transfert de chaleur est pris en compte. Vous pouvez spécifier la valeur directement ou l'obtenir à partir du nombre de Schmidt spécifié :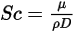
Equation 2.334
où,
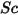 | nombre de Schmidt |
Le nombre de Schmidt représente le rapport entre le taux de diffusion visqueux et le taux de diffusion moléculaire (masse).
Si une valeur ou une fonction de température s'applique à tous les composants, l'équation 2.333 est réduite à l'expression suivante :
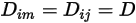
Equation 2.335
L'équation 2.335 est une approximation appropriée pour la modélisation d'un mélange dilué, avec les espèces présentes à des fractions massiques faibles dans un fluide porteur présentant une forte concentration. Dans ce cas, vous définissez 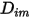 directement en tant que constante ou fonction de température.
directement en tant que constante ou fonction de température.
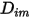 directement en tant que constante ou fonction de température.
directement en tant que constante ou fonction de température.Toutefois, pour les mélanges non dilués, avec le coefficient 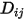 spécifié, vous utilisez l'équation 2.333 pour calculer le coefficient de diffusion massique individuel dans le mélange
spécifié, vous utilisez l'équation 2.333 pour calculer le coefficient de diffusion massique individuel dans le mélange 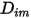 .
.
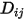 spécifié, vous utilisez l'équation 2.333 pour calculer le coefficient de diffusion massique individuel dans le mélange
spécifié, vous utilisez l'équation 2.333 pour calculer le coefficient de diffusion massique individuel dans le mélange 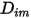 .
.◦ Théorie cinétique : pour un gaz parfait, le coefficient de diffusion massique binaire 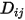 peut également être obtenu à l'aide de la théorie cinétique.
peut également être obtenu à l'aide de la théorie cinétique.
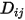 peut également être obtenu à l'aide de la théorie cinétique.
peut également être obtenu à l'aide de la théorie cinétique.Références : H. A. McGee, "Molecular Engineering", McGraw-Hill, New York, 1991.
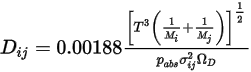
Equation 2.336
où 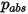 correspond à la pression absolue et
correspond à la pression absolue et 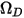 à l'intégrale de collision de diffusion, qui est une mesure de l'interaction des molécules dans le système.
à l'intégrale de collision de diffusion, qui est une mesure de l'interaction des molécules dans le système. 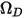 est une fonction de la grandeur
est une fonction de la grandeur 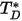 , définie comme suit :
, définie comme suit :
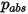 correspond à la pression absolue et
correspond à la pression absolue et 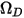 à l'intégrale de collision de diffusion, qui est une mesure de l'interaction des molécules dans le système.
à l'intégrale de collision de diffusion, qui est une mesure de l'interaction des molécules dans le système. 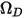 est une fonction de la grandeur
est une fonction de la grandeur 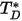 , définie comme suit :
, définie comme suit :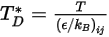
Equation 2.337
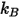 correspond à la constante de Boltzmann, qui est définie comme la constante universelle des gaz
correspond à la constante de Boltzmann, qui est définie comme la constante universelle des gaz 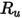 divisée par le nombre d'Avogadro.
divisée par le nombre d'Avogadro. 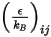 pour le mélange, correspond à la moyenne géométrique :
pour le mélange, correspond à la moyenne géométrique :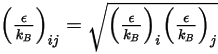
Equation 2.338
Pour un mélange binaire, 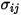 est calculé comme la moyenne arithmétique des paramètres
est calculé comme la moyenne arithmétique des paramètres 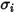 et
et 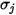 :
:
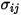 est calculé comme la moyenne arithmétique des paramètres
est calculé comme la moyenne arithmétique des paramètres 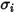 et
et 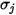 :
: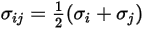
Equation 2.339
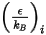 et
et 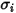 correspondent aux paramètres de Lennard-Jones du composant
correspondent aux paramètres de Lennard-Jones du composant  dans le mélange. En particulier
dans le mélange. En particulier 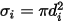 correspond à la section efficace de collision de la molécule sphérique de diamètre
correspond à la section efficace de collision de la molécule sphérique de diamètre 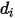 (notez qu'une molécule balaye une zone spécifiée par deux fois son diamètre, car les molécules avec lesquelles elle entre en collision ont également un diamètre
(notez qu'une molécule balaye une zone spécifiée par deux fois son diamètre, car les molécules avec lesquelles elle entre en collision ont également un diamètre 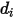 ) et
) et 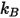 =1.38064852(79) ×10-23(J/K) à la constante de Boltzmann.
=1.38064852(79) ×10-23(J/K) à la constante de Boltzmann.Dans Creo Flow Analysis, vous spécifiez le diamètre 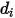 et l'énergie
et l'énergie 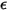 pour déterminer les deux paramètres de Lennard-Jones.
pour déterminer les deux paramètres de Lennard-Jones.
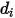 et l'énergie
et l'énergie 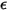 pour déterminer les deux paramètres de Lennard-Jones.
pour déterminer les deux paramètres de Lennard-Jones.◦ Coefficients de diffusion thermique 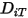 : ils peuvent être définis comme des constantes, des fonctions polynomiales de température, des fonctions définies par l'utilisateur ou à l'aide de l'expression dépendante de la composition empirique dérivée de la référence suivante :
: ils peuvent être définis comme des constantes, des fonctions polynomiales de température, des fonctions définies par l'utilisateur ou à l'aide de l'expression dépendante de la composition empirique dérivée de la référence suivante :
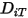 : ils peuvent être définis comme des constantes, des fonctions polynomiales de température, des fonctions définies par l'utilisateur ou à l'aide de l'expression dépendante de la composition empirique dérivée de la référence suivante :
: ils peuvent être définis comme des constantes, des fonctions polynomiales de température, des fonctions définies par l'utilisateur ou à l'aide de l'expression dépendante de la composition empirique dérivée de la référence suivante :Références : K. K. Y. Kuo, "Principles of Combustion", John Wiley and Sons, New York, 1986.
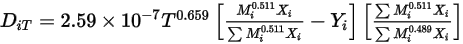
Equation 2.340
Dans cette forme du coefficient de diffusion thermique, la diffusion des molécules lourdes est plus lente, tandis que les molécules légères se diffusent plus rapidement vers les surfaces chaudes.
• Equations d'énergie cinétique
Avec les propriétés et les vitesses pondérées par la masse, les équations d'énergie cinétique pour un mélange de tous les composants sont exprimées de la même manière que celles d'écoulements mono-fluides :
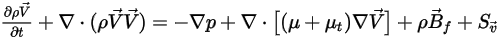
Equation 2.341
où la densité et la vitesse du mélange sont calculées à l'aide de l'équation 2.321, de l'équation 2.322 et de l'équation 2.323. La viscosité turbulente est directement calculée à partir des modèles de turbulence en fonction du mélange de l'écoulement, de sorte que sa valeur soit indépendante des composants. La viscosité laminaire est calculée comme suit :
◦ Viscosité laminaire massique moyenne : pour les mélanges de gaz réels, la viscosité du mélange est calculée sur la base d'une moyenne de la fraction massique de la viscosité des espèces chimiques (composants) pures :
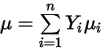
Equation 2.342
◦ Théorie cinétique : pour les mélanges de gaz parfaits, la viscosité du mélange est calculée à partir de la théorie cinétique. Pour chaque composant, la viscosité dynamique est basée sur l'équation de Boltzmann :
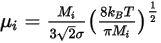
Equation 2.343
Pour la diffusivité massique, vous avez besoin des paramètres de Lennard-Jones, 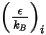 et
et 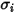 , pour calculer la viscosité des composants gazeux d'un mélange.
, pour calculer la viscosité des composants gazeux d'un mélange.
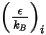 et
et 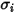 , pour calculer la viscosité des composants gazeux d'un mélange.
, pour calculer la viscosité des composants gazeux d'un mélange.La viscosité du mélange de gaz parfaits est donc calculée comme suit :
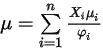
Equation 2.344
où,
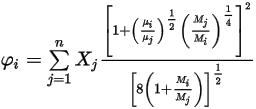
Equation 2.345
• Equation d'énergie
Comme indiqué dans le module Chaleur (Heat), l'équation d'énergie du mélange de tous les composants est exprimée comme suit :
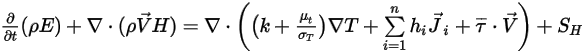
Equation 2.346
où 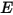 et
et 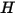 correspondent à l'énergie interne totale et à l'enthalpie totale du mélange de composants
correspondent à l'énergie interne totale et à l'enthalpie totale du mélange de composants 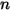 . Avec la chaleur spécifique
. Avec la chaleur spécifique 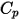 et l'enthalpie statique
et l'enthalpie statique 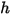 du mélange, ces données sont obtenues en établissant la moyenne massique des valeurs correspondantes de chaque composant :
du mélange, ces données sont obtenues en établissant la moyenne massique des valeurs correspondantes de chaque composant :
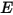 et
et 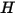 correspondent à l'énergie interne totale et à l'enthalpie totale du mélange de composants
correspondent à l'énergie interne totale et à l'enthalpie totale du mélange de composants 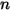 . Avec la chaleur spécifique
. Avec la chaleur spécifique 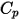 et l'enthalpie statique
et l'enthalpie statique 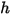 du mélange, ces données sont obtenues en établissant la moyenne massique des valeurs correspondantes de chaque composant :
du mélange, ces données sont obtenues en établissant la moyenne massique des valeurs correspondantes de chaque composant :◦ Capacité thermique massique moyenne du mélange
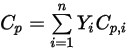
Equation 2.347
◦ Energie et enthalpie massiques moyennes du mélange
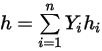
Equation 2.348
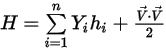
Equation 2.349
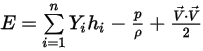
Equation 2.350
L'enthalpie statique d'un composant comporte deux parties : l'enthalpie de référence d'état standard et l'enthalpie sensible. Dans le cas d'écoulements multicomposants, vous incluez les deux parties de l'enthalpie (valeur absolue ou totale) lorsque vous calculez 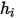 .
.
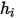 .
.Dans l'équation 2.336, le premier terme à droite représente la diffusion de l'énergie. Il se compose de trois parties : conduction thermique, transport d'énergie dû à la diffusion des espèces et échauffement visqueux. La conduction thermique du mélange est modélisée de la même manière que pour un écoulement mono-fluide. Dans Creo Flow Analysis, la conductivité thermique du mélange est calculée comme suit :
◦ Conductivité thermique massique moyenne : pour les mélanges de gaz réels, la conductivité thermique du mélange est calculée à partir d'une moyenne de fraction massique simple de la conductivité thermique des composants ou espèces purs :
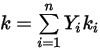
Equation 2.351
Il s'agit de la méthode par défaut dans Creo Flow Analysis.
◦ Théorie cinétique : pour les mélanges de gaz parfaits, la conductivité thermique du mélange peut être calculée en fonction de la théorie cinétique. Pour chaque composant, la conductivité thermique se présente sous la forme suivante :
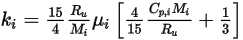
Equation 2.352
où,
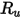 | constante universelle des gaz |
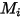 | poids moléculaire |
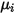 | viscosité spécifiée ou calculée du composant |
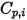 | capacité thermique spécifique calculée ou spécifiée du composant |
Notez que, à l'instar de la viscosité laminaire 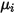 , la chaleur spécifique
, la chaleur spécifique 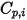 peut également être obtenue à l'aide de la théorie cinétique :
peut également être obtenue à l'aide de la théorie cinétique :
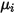 , la chaleur spécifique
, la chaleur spécifique 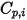 peut également être obtenue à l'aide de la théorie cinétique :
peut également être obtenue à l'aide de la théorie cinétique :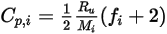
Equation 2.353
où 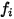 correspond au nombre de modes de stockage d'énergie (degrés de liberté) pour le composant de gaz
correspond au nombre de modes de stockage d'énergie (degrés de liberté) pour le composant de gaz  .
.
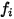 correspond au nombre de modes de stockage d'énergie (degrés de liberté) pour le composant de gaz
correspond au nombre de modes de stockage d'énergie (degrés de liberté) pour le composant de gaz  .
.La conductivité thermique du mélange de gaz parfaits est alors calculée comme suit :
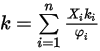
Equation 2.354
où 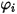 est exprimé dans l'équation 2.335.
est exprimé dans l'équation 2.335.
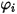 est exprimé dans l'équation 2.335.
est exprimé dans l'équation 2.335.Le second terme de diffusion,
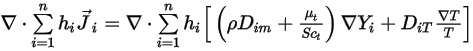
Equation 2.355
représente le transport de l'enthalpie dû à la diffusion des espèces chimiques dans l'écoulement de composants 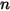 . Ce terme peut avoir un effet significatif sur l'enthalpie et ne doit pas être négligé. Lorsque le nombre de Lewis, rapport entre la diffusivité thermique
. Ce terme peut avoir un effet significatif sur l'enthalpie et ne doit pas être négligé. Lorsque le nombre de Lewis, rapport entre la diffusivité thermique 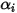 et la diffusivité massique
et la diffusivité massique 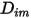 :
:
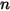 . Ce terme peut avoir un effet significatif sur l'enthalpie et ne doit pas être négligé. Lorsque le nombre de Lewis, rapport entre la diffusivité thermique
. Ce terme peut avoir un effet significatif sur l'enthalpie et ne doit pas être négligé. Lorsque le nombre de Lewis, rapport entre la diffusivité thermique 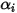 et la diffusivité massique
et la diffusivité massique 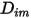 :
: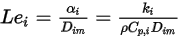
Equation 2.356
pour toute espèce n'est pas une unité, le fait de négliger ce terme peut entraîner des erreurs importantes.
Le troisième terme de diffusion correspond à la contribution de l'échauffement visqueux 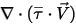 . Bien que le traitement soit le même que pour un écoulement mono-fluide, vous calculez la contrainte de cisaillement
. Bien que le traitement soit le même que pour un écoulement mono-fluide, vous calculez la contrainte de cisaillement 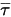 à l'aide des viscosités laminaire et turbulente du mélange. Le terme source général
à l'aide des viscosités laminaire et turbulente du mélange. Le terme source général 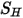 correspond à la source de chaleur externe/utilisateur totale sur tous les composants.
correspond à la source de chaleur externe/utilisateur totale sur tous les composants.
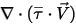 . Bien que le traitement soit le même que pour un écoulement mono-fluide, vous calculez la contrainte de cisaillement
. Bien que le traitement soit le même que pour un écoulement mono-fluide, vous calculez la contrainte de cisaillement 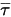 à l'aide des viscosités laminaire et turbulente du mélange. Le terme source général
à l'aide des viscosités laminaire et turbulente du mélange. Le terme source général 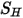 correspond à la source de chaleur externe/utilisateur totale sur tous les composants.
correspond à la source de chaleur externe/utilisateur totale sur tous les composants.• Modèles de turbulence : avec la densité du mélange 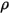 , la viscosité moléculaire
, la viscosité moléculaire 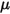 et la vitesse
et la vitesse 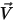 , les équations de modélisation de la turbulence dans les modèles k-ε standard et k-ε RNG présentent les mêmes formes générales que dans les modèles de turbulence mono-fluide. Ces derniers sont décrits dans le module Turbulence (Turbulence). La viscosité turbulente du mélange,
, les équations de modélisation de la turbulence dans les modèles k-ε standard et k-ε RNG présentent les mêmes formes générales que dans les modèles de turbulence mono-fluide. Ces derniers sont décrits dans le module Turbulence (Turbulence). La viscosité turbulente du mélange, 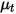 , est directement calculée à partir de l'expression :
, est directement calculée à partir de l'expression :
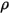 , la viscosité moléculaire
, la viscosité moléculaire 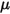 et la vitesse
et la vitesse 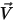 , les équations de modélisation de la turbulence dans les modèles k-ε standard et k-ε RNG présentent les mêmes formes générales que dans les modèles de turbulence mono-fluide. Ces derniers sont décrits dans le module Turbulence (Turbulence). La viscosité turbulente du mélange,
, les équations de modélisation de la turbulence dans les modèles k-ε standard et k-ε RNG présentent les mêmes formes générales que dans les modèles de turbulence mono-fluide. Ces derniers sont décrits dans le module Turbulence (Turbulence). La viscosité turbulente du mélange, 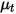 , est directement calculée à partir de l'expression :
, est directement calculée à partir de l'expression :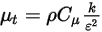
Equation 2.357
Par ailleurs, la production d'énergie cinétique turbulente est calculée en fonction des gradients de vitesse et de viscosité turbulente du mélange.
Modélisation des frontières multicomposants
Dans un écoulement multicomposant, les conditions aux limites des équations de modélisation des turbulences, de l'énergie et des écoulements sont identiques à celles des écoulements monophasiques décrits dans les modules Ecoulement (Flow), Chaleur (Heat) et Turbulence (Turbulence). Pour les fractions massiques d'un composant, les conditions aux limites sont constituées d'une valeur spécifiée, d'un flux volumétrique spécifié et/ou d'un gradient.
• Frontière d'entrée n composants
Au niveau d'une frontière d'entrée, le transport net d'un composant peut comporter à la fois des contributions de convection et de diffusion. La convection est déterminée par la fraction massique des espèces d'entrée spécifiées. La diffusion dépend du gradient du champ de fraction massique calculé. Lorsque les vitesses d'admission de convection sont très basses, une masse substantielle peut être gagnée ou perdue via l'entrée, en raison de la diffusion. Pour cette raison, la diffusion d'entrée n'est pas incluse par défaut, mais peut être activée en option.
◦ Valeur spécifiée : pour l'écoulement de composants 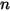 , les fractions massiques d'entrée sont prédéterminées pour les composants
, les fractions massiques d'entrée sont prédéterminées pour les composants 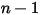 , tandis que la fraction massique du composant
, tandis que la fraction massique du composant 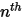 est obtenue à l'aide de l'équation 2.319 de contrainte physique :
est obtenue à l'aide de l'équation 2.319 de contrainte physique :
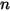 , les fractions massiques d'entrée sont prédéterminées pour les composants
, les fractions massiques d'entrée sont prédéterminées pour les composants 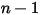 , tandis que la fraction massique du composant
, tandis que la fraction massique du composant 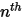 est obtenue à l'aide de l'équation 2.319 de contrainte physique :
est obtenue à l'aide de l'équation 2.319 de contrainte physique :
Equation 2.358
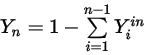
Equation 2.359
De plus, la fraction massique de chaque composant ne doit pas être négative.
◦ Flux volumétrique spécifié : en supposant que 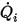 est le flux volumétrique d'entrée prédéterminé pour le composant
est le flux volumétrique d'entrée prédéterminé pour le composant  , vous disposez du flux massique de chaque composant
, vous disposez du flux massique de chaque composant 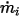 et du flux massique total à l'entrée
et du flux massique total à l'entrée 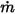 comme suit :
comme suit :
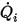 est le flux volumétrique d'entrée prédéterminé pour le composant
est le flux volumétrique d'entrée prédéterminé pour le composant  , vous disposez du flux massique de chaque composant
, vous disposez du flux massique de chaque composant 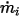 et du flux massique total à l'entrée
et du flux massique total à l'entrée 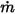 comme suit :
comme suit :
Equation 2.360
où 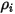 correspond à la densité d'entrée du composant
correspond à la densité d'entrée du composant  .
.
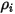 correspond à la densité d'entrée du composant
correspond à la densité d'entrée du composant  .
.Par définition, la fraction massique est calculée comme suit :
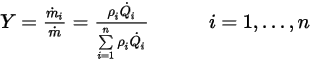
Equation 2.361
◦ Frontière de sortie/symétrie/paroi : pour les composants 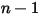 , les conditions de gradient zéro s'appliquent à toutes les frontières de sortie, de symétrie et de paroi, tandis que la phase
, les conditions de gradient zéro s'appliquent à toutes les frontières de sortie, de symétrie et de paroi, tandis que la phase 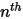 est obtenue à l'aide de la contrainte physique :
est obtenue à l'aide de la contrainte physique :
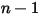 , les conditions de gradient zéro s'appliquent à toutes les frontières de sortie, de symétrie et de paroi, tandis que la phase
, les conditions de gradient zéro s'appliquent à toutes les frontières de sortie, de symétrie et de paroi, tandis que la phase 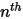 est obtenue à l'aide de la contrainte physique :
est obtenue à l'aide de la contrainte physique :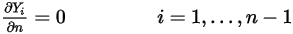
Equation 2.362
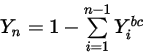
Equation 2.363
où 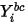 correspond à la valeur de frontière obtenue par l'équation 2.347.
correspond à la valeur de frontière obtenue par l'équation 2.347.
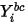 correspond à la valeur de frontière obtenue par l'équation 2.347.
correspond à la valeur de frontière obtenue par l'équation 2.347.Considérations numériques
Les équations principales, les modèles de turbulence et les conditions aux limites ci-dessus constituent la base du modèle de mélange multicomposant. Sans termes sources externes ou utilisateur, ni de réactions chimiques, ils forment un système d'équations fermé que vous résolvez numériquement à l'aide d'un solveur volumes finis basé sur la pression.
Les équations de transport pour les fractions massiques sont résolues pour tous les composants. Pour satisfaire à la contrainte physique, les fractions massiques réelles sont mises à l'échelle à l'aide de la somme des valeurs résolues pour tous les composants :

Equation 2.364
où 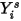 correspond à la valeur obtenue par la résolution de l'équation 2.320. La fraction massique réelle est la suivante :
correspond à la valeur obtenue par la résolution de l'équation 2.320. La fraction massique réelle est la suivante :
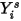 correspond à la valeur obtenue par la résolution de l'équation 2.320. La fraction massique réelle est la suivante :
correspond à la valeur obtenue par la résolution de l'équation 2.320. La fraction massique réelle est la suivante :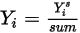
Equation 2.365