Solveur d'EDO
Les équations différentielles ordinaires (ODE) 2.432 et 2.444, qui régissent respectivement la translation et la rotation 1 DDL des frontières et des volumes, sont résolues numériquement dans Creo Flow Analysis. Plus précisément, pour calculer le mouvement et le déplacement d'une frontière et d'un volume à des fins de remaillage, les schémas de pas de temps suivants sont adoptés pour intégrer les EDO : solveur explicite raide, d'Euler ou Runge-Kutta.
Intégration d'une équation de translation à 1 DDL
En intégrant les équations 2.434, 2.435 et 2.436 à l'équation 2.432 et en regroupant des termes de force explicites en un terme unique (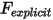 , par souci de concision), vous réécrivez l'équation de mouvement de translation à 1 DDL sous la forme suivante :
, par souci de concision), vous réécrivez l'équation de mouvement de translation à 1 DDL sous la forme suivante :
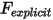 , par souci de concision), vous réécrivez l'équation de mouvement de translation à 1 DDL sous la forme suivante :
, par souci de concision), vous réécrivez l'équation de mouvement de translation à 1 DDL sous la forme suivante :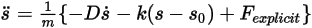
Equation 2.455
où le terme de force calculé explicitement 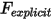 est :
est :
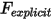 est :
est :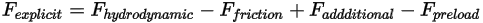
Equation 2.456
Avec les conditions initiales et aux limites données, le déplacement du corps solide est obtenu en intégrant l'équation 2.455 à l'aide de schémas de pas de temps explicites. Pour le pas de temps 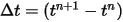 , vous disposez des formules générales suivantes :
, vous disposez des formules générales suivantes :
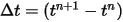 , vous disposez des formules générales suivantes :
, vous disposez des formules générales suivantes :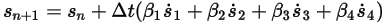
Equation 2.457
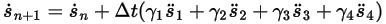
Equation 2.458
où les facteurs de chargement totalisent 1 :
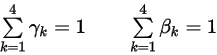
Equation 2.459
Avec le choix des facteurs de chargement, différents schémas sont dérivés. Par exemple, les schémas explicites d'Euler et de Runge-Kutta sont les suivants :
• Méthode explicite d'Euler (premier ordre)
Avec 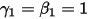 et
et 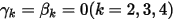 , vous disposez du schéma explicite d'Euler dans les éléments suivants :
, vous disposez du schéma explicite d'Euler dans les éléments suivants :
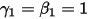 et
et 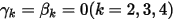 , vous disposez du schéma explicite d'Euler dans les éléments suivants :
, vous disposez du schéma explicite d'Euler dans les éléments suivants :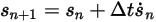
Equation 2.460
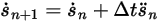
Equation 2.461
• Solveur explicite Runge-Kutta
Les solveurs Runge-Kutta sont des schémas explicites de deuxième et de quatrième ordre. Les voici :
◦ Schéma du deuxième ordre
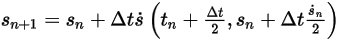
Equation 2.462
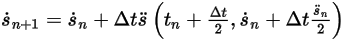
Equation 2.463
◦ Schéma du quatrième ordre
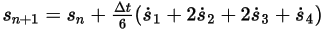
Equation 2.464
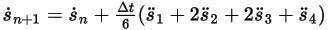
Equation 2.465
où,

Equation 2.466

Equation 2.467

Equation 2.468

Equation 2.469
• Solveur raide (explicite)
Outre les schémas standard d'Euler et Runge-Kutta, Creo Flow Analysis a développé son solveur raide pour intégrer l'EDO de translation à 1-DDL. Il s'agit de la méthode par défaut pour les mouvements dynamiques des corps solides.
Intégration d'une équation de rotation à 1 DDL
En ce qui concerne la translation, en intégrant les équations 2.446 et 2.447 à l'équation 2.444 et en regroupant des termes de couple explicites en un seul terme (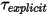 , par souci de concision), vous réécrivez l'équation de mouvement de rotation à 1-DDL (équation 2.444) sous la forme suivante :
, par souci de concision), vous réécrivez l'équation de mouvement de rotation à 1-DDL (équation 2.444) sous la forme suivante :
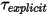 , par souci de concision), vous réécrivez l'équation de mouvement de rotation à 1-DDL (équation 2.444) sous la forme suivante :
, par souci de concision), vous réécrivez l'équation de mouvement de rotation à 1-DDL (équation 2.444) sous la forme suivante :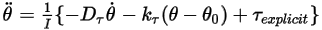
Equation 2.470
où le terme de couple calculé explicitement 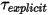 est :
est :
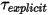 est :
est :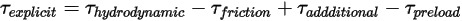
Equation 2.471
Avec les conditions initiales et aux limites données, l'angle de rotation est obtenu en intégrant l'équation 2.470 à l'aide de schémas de pas de temps explicites. Pour le pas de temps 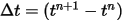 , vous disposez des formules générales suivantes :
, vous disposez des formules générales suivantes :
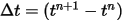 , vous disposez des formules générales suivantes :
, vous disposez des formules générales suivantes :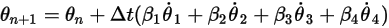
Equation 2.472
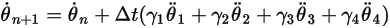
Equation 2.473
où les facteurs de chargement totalisent 1 :
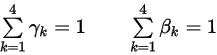
Equation 2.474
Avec le choix des facteurs de chargement, différents schémas numériques sont facilement dérivés. Voici encore une fois les schémas explicites d'Euler et Runge-Kutta :
• Méthode explicite d'Euler (premier ordre)
Avec 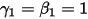 et
et 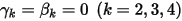 , vous disposez du schéma explicite d'Euler dans les éléments suivants :
, vous disposez du schéma explicite d'Euler dans les éléments suivants :
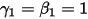 et
et 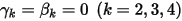 , vous disposez du schéma explicite d'Euler dans les éléments suivants :
, vous disposez du schéma explicite d'Euler dans les éléments suivants :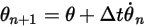
Equation 2.475
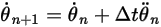
Equation 2.476
• Solveur explicite Runge-Kutta
Les solveurs Runge-Kutta sont des schémas explicites de deuxième et de quatrième ordre. Les voici :
◦ Schéma du deuxième ordre
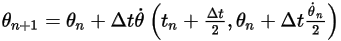
Equation 2.477
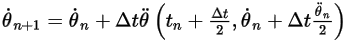
Equation 2.478
◦ Schéma du quatrième ordre
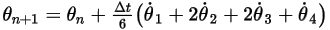
Equation 2.479
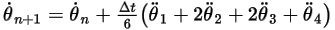
Equation 2.480
où,

Equation 2.481

Equation 2.482

Equation 2.483

Equation 2.484
• Solveur raide (explicite)
Outre les schémas standard d'Euler et Runge-Kutta, Creo Flow Analysis a développé son solveur raide pour intégrer l'EDO de translation à 1 DDL (équation 2.444). Il s'agit de la méthode par défaut pour les mouvements dynamiques des corps solides.