Mouvements d'un corps rigide
Dans les simulations, les surfaces d'un objet solide sont généralement des frontières de paroi dans un domaine d'écoulement. Lorsqu'un objet ou une surface solide est soumis à des forces dynamiques et mécaniques, et à un effet thermique, le déséquilibre des forces nettes peut entraîner le déplacement et la déformation du corps. Un objet solide est souvent considéré comme un corps rigide dans les simulations d'écoulement. Par conséquent, pour un objet solide soumis à des déséquilibres de force, vous supposez qu'il peut se déplacer de manière linéaire (translation), de manière angulaire (rotation) ou à la fois de manière linéaire et angulaire, sans déformation. Toutefois, dans le cas d'un domaine de calculs CFA, le déplacement des frontières peut entraîner la modification du domaine et, par conséquent, le maillage du volume peut se déformer, comme décrit dans le module Ecoulement (Flow).
Dans le cas d'un corps rigide, les équations qui régissent ses mouvements sont directement dérivées de la conservation du moment linéaire et angulaire :
• Moment linéaire (translation)
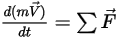
Equation 2.426
• Moment angulaire (rotation)
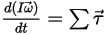
Equation 2.427
Dans l'équation 2.426, 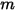 correspond à la masse de l'objet en mouvement,
correspond à la masse de l'objet en mouvement, 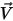 ⃗ à la vitesse linéaire/transitoire et
⃗ à la vitesse linéaire/transitoire et 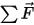 ⃗ aux forces totales/nettes exercées sur le corps en translation. Dans l'équation 2.427,
⃗ aux forces totales/nettes exercées sur le corps en translation. Dans l'équation 2.427, 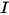 correspond au moment d'inertie,
correspond au moment d'inertie, 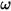 ⃗ à la vitesse angulaire et
⃗ à la vitesse angulaire et 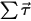 ⃗ au couple total/net exercé sur le corps en rotation.
⃗ au couple total/net exercé sur le corps en rotation.
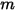 correspond à la masse de l'objet en mouvement,
correspond à la masse de l'objet en mouvement, 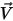 ⃗ à la vitesse linéaire/transitoire et
⃗ à la vitesse linéaire/transitoire et 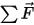 ⃗ aux forces totales/nettes exercées sur le corps en translation. Dans l'équation 2.427,
⃗ aux forces totales/nettes exercées sur le corps en translation. Dans l'équation 2.427, 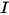 correspond au moment d'inertie,
correspond au moment d'inertie, 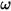 ⃗ à la vitesse angulaire et
⃗ à la vitesse angulaire et 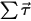 ⃗ au couple total/net exercé sur le corps en rotation.
⃗ au couple total/net exercé sur le corps en rotation.L'équation 2.426 et l'équation 2.427 régissent les mouvements généraux d'un corps solide, qui dispose de six degrés de liberté avec trois degrés chacun pour la translation et la rotation, respectivement. Creo Flow Analysis ne prend en compte qu'un degré de liberté de translation et de rotation. Ceux-ci sont expliqués dans cette section.
Translation - Un degré de liberté
En supposant qu'un corps solide se déplace de manière linéaire dans une direction arbitraire (qui ne change pas), définie par un vecteur unitaire 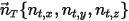 , le mouvement de translation du corps est réduit à un degré de liberté. Par conséquent, pour conserver le moment linéaire, l'équation 2.426 devient une équation scalaire suivant la direction du mouvement, la vitesse et la force de déplacement étant exprimées par
, le mouvement de translation du corps est réduit à un degré de liberté. Par conséquent, pour conserver le moment linéaire, l'équation 2.426 devient une équation scalaire suivant la direction du mouvement, la vitesse et la force de déplacement étant exprimées par 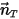 :
:
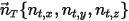 , le mouvement de translation du corps est réduit à un degré de liberté. Par conséquent, pour conserver le moment linéaire, l'équation 2.426 devient une équation scalaire suivant la direction du mouvement, la vitesse et la force de déplacement étant exprimées par
, le mouvement de translation du corps est réduit à un degré de liberté. Par conséquent, pour conserver le moment linéaire, l'équation 2.426 devient une équation scalaire suivant la direction du mouvement, la vitesse et la force de déplacement étant exprimées par 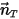 :
: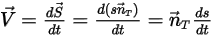
Equation 2.428
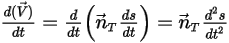
Equation 2.429
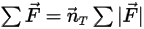
Equation 2.430
où 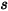 correspond à l'amplitude du vecteur position
correspond à l'amplitude du vecteur position 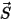 à un point d'intérêt sur le corps solide suivant la direction du mouvement
à un point d'intérêt sur le corps solide suivant la direction du mouvement 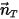 . Dans un repère cartésien, vous obtenez :
. Dans un repère cartésien, vous obtenez :
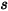 correspond à l'amplitude du vecteur position
correspond à l'amplitude du vecteur position 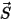 à un point d'intérêt sur le corps solide suivant la direction du mouvement
à un point d'intérêt sur le corps solide suivant la direction du mouvement 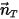 . Dans un repère cartésien, vous obtenez :
. Dans un repère cartésien, vous obtenez :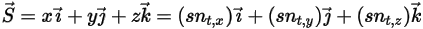
Equation 2.431
Si la masse du corps solide reste constante et que vous développez le terme de force pour inclure explicitement toutes les forces appliquées au corps, vous obtenez l'équation scalaire du moment linéaire suivante :
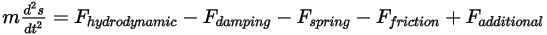
Equation 2.432
Les forces à droite indiquent les éléments suivants :
• Force hydrodynamique  : comprend les forces de pression et de cisaillement. Celles-ci sont dues au mouvement relatif entre l'écoulement de fluide et les surfaces du corps solide en contact avec cet écoulement. Les forces de pression et de cisaillement sont obtenues à partir des solutions d'écoulement (grandeurs de sortie) :
: comprend les forces de pression et de cisaillement. Celles-ci sont dues au mouvement relatif entre l'écoulement de fluide et les surfaces du corps solide en contact avec cet écoulement. Les forces de pression et de cisaillement sont obtenues à partir des solutions d'écoulement (grandeurs de sortie) :
 : comprend les forces de pression et de cisaillement. Celles-ci sont dues au mouvement relatif entre l'écoulement de fluide et les surfaces du corps solide en contact avec cet écoulement. Les forces de pression et de cisaillement sont obtenues à partir des solutions d'écoulement (grandeurs de sortie) :
: comprend les forces de pression et de cisaillement. Celles-ci sont dues au mouvement relatif entre l'écoulement de fluide et les surfaces du corps solide en contact avec cet écoulement. Les forces de pression et de cisaillement sont obtenues à partir des solutions d'écoulement (grandeurs de sortie) :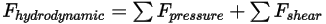
Equation 2.433
• Force d'amortissement 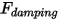 : force de retardement causée par l'effet d'amortissement du frottement. Elle est déterminée par le mouvement de l'objet solide et le coefficient d'amortissement défini par l'utilisateur
: force de retardement causée par l'effet d'amortissement du frottement. Elle est déterminée par le mouvement de l'objet solide et le coefficient d'amortissement défini par l'utilisateur 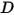 :
:
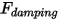 : force de retardement causée par l'effet d'amortissement du frottement. Elle est déterminée par le mouvement de l'objet solide et le coefficient d'amortissement défini par l'utilisateur
: force de retardement causée par l'effet d'amortissement du frottement. Elle est déterminée par le mouvement de l'objet solide et le coefficient d'amortissement défini par l'utilisateur 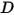 :
: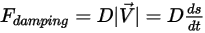
Equation 2.434
• Force de ressort 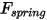 : dépend du déplacement du ressort
: dépend du déplacement du ressort 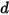 , de la constante de rappel
, de la constante de rappel 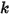 et de la force de précharge
et de la force de précharge 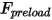 :
:
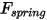 : dépend du déplacement du ressort
: dépend du déplacement du ressort 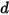 , de la constante de rappel
, de la constante de rappel 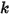 et de la force de précharge
et de la force de précharge 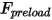 :
: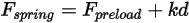
Equation 2.435
où le déplacement du ressort 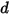 est défini comme suit :
est défini comme suit :
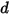 est défini comme suit :
est défini comme suit :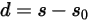
Equation 2.436
où 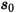 correspond à l'amplitude du vecteur position
correspond à l'amplitude du vecteur position 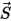 à la position précédente
à la position précédente 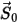 .
.
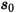 correspond à l'amplitude du vecteur position
correspond à l'amplitude du vecteur position 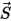 à la position précédente
à la position précédente 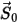 .
.• Force de frottement : le modèle de frottement de contact est adopté pour prendre en compte l'effet de frottement dans un système dynamique. La force de frottement 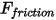 est modélisée comme suit :
est modélisée comme suit :
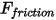 est modélisée comme suit :
est modélisée comme suit :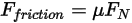
Equation 2.437
où 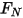 est la composante normale de la force de contact exercée sur la surface solide d'intérêt. Pour le coefficient de frottement
est la composante normale de la force de contact exercée sur la surface solide d'intérêt. Pour le coefficient de frottement 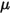 , le coefficient de frottement statique
, le coefficient de frottement statique 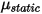 et le coefficient de frottement par glissement
et le coefficient de frottement par glissement 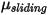 sont également introduits pour les corps immobiles et mobiles, respectivement :
sont également introduits pour les corps immobiles et mobiles, respectivement :
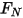 est la composante normale de la force de contact exercée sur la surface solide d'intérêt. Pour le coefficient de frottement
est la composante normale de la force de contact exercée sur la surface solide d'intérêt. Pour le coefficient de frottement 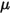 , le coefficient de frottement statique
, le coefficient de frottement statique 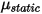 et le coefficient de frottement par glissement
et le coefficient de frottement par glissement 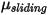 sont également introduits pour les corps immobiles et mobiles, respectivement :
sont également introduits pour les corps immobiles et mobiles, respectivement :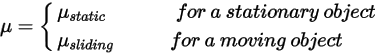
Equation 2.438
• Force supplémentaire 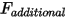 : ajoutée pour les forces supplémentaires spécifiées par l'utilisateur.
: ajoutée pour les forces supplémentaires spécifiées par l'utilisateur.
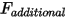 : ajoutée pour les forces supplémentaires spécifiées par l'utilisateur.
: ajoutée pour les forces supplémentaires spécifiées par l'utilisateur.Rotation - Un degré de liberté
Lorsqu'un axe de rotation arbitraire est défini par un point (centre de l'axe) 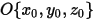 et le vecteur unitaire de direction
et le vecteur unitaire de direction 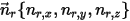 , la rotation du corps solide autour de l'axe
, la rotation du corps solide autour de l'axe 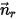 est également limitée à un degré de liberté. De même, pour conserver le moment angulaire, l'équation 2.427 devient également une équation scalaire suivant la direction tangentielle
est également limitée à un degré de liberté. De même, pour conserver le moment angulaire, l'équation 2.427 devient également une équation scalaire suivant la direction tangentielle 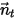 , définie comme suit :
, définie comme suit :
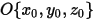 et le vecteur unitaire de direction
et le vecteur unitaire de direction 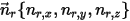 , la rotation du corps solide autour de l'axe
, la rotation du corps solide autour de l'axe 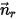 est également limitée à un degré de liberté. De même, pour conserver le moment angulaire, l'équation 2.427 devient également une équation scalaire suivant la direction tangentielle
est également limitée à un degré de liberté. De même, pour conserver le moment angulaire, l'équation 2.427 devient également une équation scalaire suivant la direction tangentielle 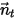 , définie comme suit :
, définie comme suit :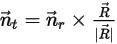
Equation 2.439
où 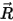 correspond au vecteur pointant depuis le centre de l'axe vers un point arbitraire
correspond au vecteur pointant depuis le centre de l'axe vers un point arbitraire 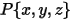 du corps solide :
du corps solide :
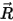 correspond au vecteur pointant depuis le centre de l'axe vers un point arbitraire
correspond au vecteur pointant depuis le centre de l'axe vers un point arbitraire 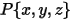 du corps solide :
du corps solide :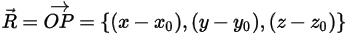
Equation 2.440
La vitesse angulaire et le couple au point 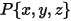 sont reformulés comme suit :
sont reformulés comme suit :
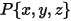 sont reformulés comme suit :
sont reformulés comme suit :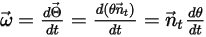
Equation 2.441
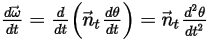
Equation 2.442
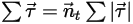
Equation 2.443
où 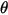 correspond à l'angle de rotation du point
correspond à l'angle de rotation du point 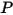 par rapport à la position de départ ou de référence.
par rapport à la position de départ ou de référence.
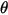 correspond à l'angle de rotation du point
correspond à l'angle de rotation du point 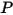 par rapport à la position de départ ou de référence.
par rapport à la position de départ ou de référence.Si le moment d'inertie reste constant et que vous développez le terme de couple pour inclure explicitement tous les couples appliqués au corps en rotation, vous obtenez l'équation scalaire du moment angulaire suivante :
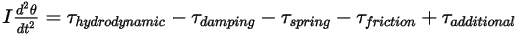
Equation 2.444
Les termes de couple à droite sont définis comme suit :
• Couple hydrodynamique 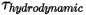 : combinaison de couple dû aux forces de pression et de cisaillement :
: combinaison de couple dû aux forces de pression et de cisaillement :
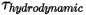 : combinaison de couple dû aux forces de pression et de cisaillement :
: combinaison de couple dû aux forces de pression et de cisaillement :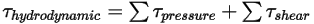
Equation 2.445
• Couple d'amortissement 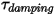 : dépend de la vitesse de rotation
: dépend de la vitesse de rotation 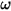 et du coefficient d'amortissement défini par l'utilisateur
et du coefficient d'amortissement défini par l'utilisateur 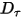 :
:
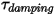 : dépend de la vitesse de rotation
: dépend de la vitesse de rotation 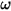 et du coefficient d'amortissement défini par l'utilisateur
et du coefficient d'amortissement défini par l'utilisateur 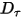 :
: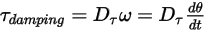
Equation 2.446
• Couple de ressort 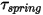 : couple induit par la torsion qui dépend de l'angle de déplacement
: couple induit par la torsion qui dépend de l'angle de déplacement 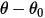 , du couple de précharge défini par l'utilisateur
, du couple de précharge défini par l'utilisateur 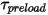 et de la constante de torsion
et de la constante de torsion 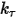 .
.
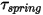 : couple induit par la torsion qui dépend de l'angle de déplacement
: couple induit par la torsion qui dépend de l'angle de déplacement 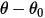 , du couple de précharge défini par l'utilisateur
, du couple de précharge défini par l'utilisateur 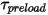 et de la constante de torsion
et de la constante de torsion 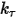 .
.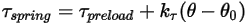
Equation 2.447
où 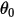 correspond à l'angle de référence. Il s'agit généralement de la position de la frontière ou du volume pendant la configuration du modèle, mais cela peut correspondre à une autre position. Par exemple, sur un déplacement angulaire nul, l'angle de référence
correspond à l'angle de référence. Il s'agit généralement de la position de la frontière ou du volume pendant la configuration du modèle, mais cela peut correspondre à une autre position. Par exemple, sur un déplacement angulaire nul, l'angle de référence 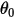 n'est pas identique à la position angulaire initiale.
n'est pas identique à la position angulaire initiale.
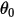 correspond à l'angle de référence. Il s'agit généralement de la position de la frontière ou du volume pendant la configuration du modèle, mais cela peut correspondre à une autre position. Par exemple, sur un déplacement angulaire nul, l'angle de référence
correspond à l'angle de référence. Il s'agit généralement de la position de la frontière ou du volume pendant la configuration du modèle, mais cela peut correspondre à une autre position. Par exemple, sur un déplacement angulaire nul, l'angle de référence 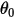 n'est pas identique à la position angulaire initiale.
n'est pas identique à la position angulaire initiale.• Couple de frottement : couple causé par la force de frottement qui se produit lorsque deux objets en contact se déplacent. Dans les expériences, il est déterminé par la différence entre le couple appliqué et le couple observé ou net. Cela dépend du coefficient de frottement 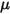 et du couple de contact en raison de la force normale
et du couple de contact en raison de la force normale 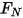 appliquée sur la surface de contact :
appliquée sur la surface de contact :
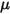 et du couple de contact en raison de la force normale
et du couple de contact en raison de la force normale 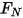 appliquée sur la surface de contact :
appliquée sur la surface de contact :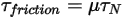
Equation 2.448
où 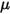 correspond à un paramètre défini par l'utilisateur, défini dans l'équation 2.438.
correspond à un paramètre défini par l'utilisateur, défini dans l'équation 2.438.
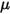 correspond à un paramètre défini par l'utilisateur, défini dans l'équation 2.438.
correspond à un paramètre défini par l'utilisateur, défini dans l'équation 2.438.• Couples supplémentaires 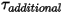 : ajoutés pour les couples supplémentaires spécifiés par l'utilisateur.
: ajoutés pour les couples supplémentaires spécifiés par l'utilisateur.
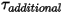 : ajoutés pour les couples supplémentaires spécifiés par l'utilisateur.
: ajoutés pour les couples supplémentaires spécifiés par l'utilisateur.Modèle de rebond
Dans de nombreux cas, un corps solide translate et/ou pivote dans un espace limité (distance ou angle limité), à savoir qu'il a une position maximale et/ou minimale. Par exemple, comme illustré par la figure suivante, lorsqu'un pendule de gravité simple est lancé de la position d'origine avec l'angle 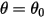 , la force de rappel agissant sur sa masse entraîne l'oscillation par rapport à la position d'équilibre. L'angle maximal de chaque côté de la position d'équilibre
, la force de rappel agissant sur sa masse entraîne l'oscillation par rapport à la position d'équilibre. L'angle maximal de chaque côté de la position d'équilibre 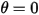 dépend de sa position de lancement
dépend de sa position de lancement 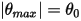 . En l'absence de frottement (pivot sans frottement et dans le vide), l'angle maximum reste inchangé et le pendule se balance indéfiniment d'avant en arrière en conservant les mêmes positions extrêmes. Toutefois, lorsqu'un pendule est lancé dans l'atmosphère, par exemple, la résistance de l'air (amortissement) entraîne une réduction progressive de l'angle maximal de balancement avant un arrêt à la position d'équilibre.
. En l'absence de frottement (pivot sans frottement et dans le vide), l'angle maximum reste inchangé et le pendule se balance indéfiniment d'avant en arrière en conservant les mêmes positions extrêmes. Toutefois, lorsqu'un pendule est lancé dans l'atmosphère, par exemple, la résistance de l'air (amortissement) entraîne une réduction progressive de l'angle maximal de balancement avant un arrêt à la position d'équilibre.
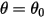 , la force de rappel agissant sur sa masse entraîne l'oscillation par rapport à la position d'équilibre. L'angle maximal de chaque côté de la position d'équilibre
, la force de rappel agissant sur sa masse entraîne l'oscillation par rapport à la position d'équilibre. L'angle maximal de chaque côté de la position d'équilibre 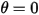 dépend de sa position de lancement
dépend de sa position de lancement 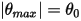 . En l'absence de frottement (pivot sans frottement et dans le vide), l'angle maximum reste inchangé et le pendule se balance indéfiniment d'avant en arrière en conservant les mêmes positions extrêmes. Toutefois, lorsqu'un pendule est lancé dans l'atmosphère, par exemple, la résistance de l'air (amortissement) entraîne une réduction progressive de l'angle maximal de balancement avant un arrêt à la position d'équilibre.
. En l'absence de frottement (pivot sans frottement et dans le vide), l'angle maximum reste inchangé et le pendule se balance indéfiniment d'avant en arrière en conservant les mêmes positions extrêmes. Toutefois, lorsqu'un pendule est lancé dans l'atmosphère, par exemple, la résistance de l'air (amortissement) entraîne une réduction progressive de l'angle maximal de balancement avant un arrêt à la position d'équilibre.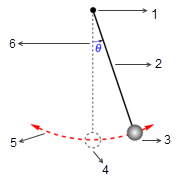
figure
1. Pivot sans frottement
2. Tige sans masse
3. Lentille avec masse
4. Position d'équilibre
5. Trajectoire de la lentille
6. Amplitude
En outre, dans un cycle de balancement (période), lorsque le pendule atteint la position la plus élevée 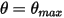 , il change de direction avec une perte totale de son énergie cinétique. Avec un pendule de gravité simple, l'énergie cinétique est complètement transférée en énergie potentielle, tandis que, lorsque vous tenez compte de la résistance du milieu, une partie de l'énergie cinétique est perdue pour surmonter l'amortissement visqueux. Toutefois, la force nette ou l'énergie potentielle inverse le balancement du pendule vers la position d'équilibre, où l'énergie cinétique (vitesse) est au maximum et l'énergie potentielle au minimum. Dans ce cas,
, il change de direction avec une perte totale de son énergie cinétique. Avec un pendule de gravité simple, l'énergie cinétique est complètement transférée en énergie potentielle, tandis que, lorsque vous tenez compte de la résistance du milieu, une partie de l'énergie cinétique est perdue pour surmonter l'amortissement visqueux. Toutefois, la force nette ou l'énergie potentielle inverse le balancement du pendule vers la position d'équilibre, où l'énergie cinétique (vitesse) est au maximum et l'énergie potentielle au minimum. Dans ce cas, 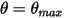 indique l'absence de rebond pour l'équation 2.444 de moment angulaire à un degré de liberté.
indique l'absence de rebond pour l'équation 2.444 de moment angulaire à un degré de liberté.
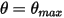 , il change de direction avec une perte totale de son énergie cinétique. Avec un pendule de gravité simple, l'énergie cinétique est complètement transférée en énergie potentielle, tandis que, lorsque vous tenez compte de la résistance du milieu, une partie de l'énergie cinétique est perdue pour surmonter l'amortissement visqueux. Toutefois, la force nette ou l'énergie potentielle inverse le balancement du pendule vers la position d'équilibre, où l'énergie cinétique (vitesse) est au maximum et l'énergie potentielle au minimum. Dans ce cas,
, il change de direction avec une perte totale de son énergie cinétique. Avec un pendule de gravité simple, l'énergie cinétique est complètement transférée en énergie potentielle, tandis que, lorsque vous tenez compte de la résistance du milieu, une partie de l'énergie cinétique est perdue pour surmonter l'amortissement visqueux. Toutefois, la force nette ou l'énergie potentielle inverse le balancement du pendule vers la position d'équilibre, où l'énergie cinétique (vitesse) est au maximum et l'énergie potentielle au minimum. Dans ce cas, 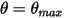 indique l'absence de rebond pour l'équation 2.444 de moment angulaire à un degré de liberté.
indique l'absence de rebond pour l'équation 2.444 de moment angulaire à un degré de liberté.En plus de cette condition, un corps mobile à la position limite peut ne pas perdre d'énergie cinétique et rebondir (rebond parfait) ou ne perdre qu'une partie de son énergie cinétique (rebond partiel). Par conséquent, les trois conditions de rebond suivantes sont appliquées lorsque les équations de la dynamique de translation et de rotation (un degré de liberté) (équation 2.432 et équation 2.444) sont résolues pour déterminer les mouvements d'un corps solide ou d'une frontière de paroi pour le domaine découlement :
• Aucun rebond : modèle par défaut dans Creo Flow Analysis. Cela permet de déterminer que, lorsqu'un corps solide ou une frontière atteint la limite de son mouvement, il/elle change de direction avec la perte totale de son énergie cinétique. Avec 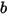 et
et  représentant le rebond et l'incidence, et
représentant le rebond et l'incidence, et 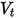 et
et 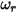 la vitesse de translation et de rotation (amplitude uniquement), ce modèle de rebond est exprimé comme suit :
la vitesse de translation et de rotation (amplitude uniquement), ce modèle de rebond est exprimé comme suit :
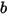 et
et  représentant le rebond et l'incidence, et
représentant le rebond et l'incidence, et 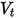 et
et 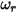 la vitesse de translation et de rotation (amplitude uniquement), ce modèle de rebond est exprimé comme suit :
la vitesse de translation et de rotation (amplitude uniquement), ce modèle de rebond est exprimé comme suit :◦ Translation
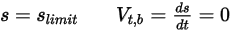
Equation 2.449
◦ Rotation
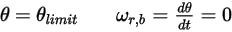
Equation 2.450
• Rebond partiel : modèle qui détermine que, lorsqu'un corps solide ou une frontière atteint la limite de son mouvement, il/elle change de direction avec une perte partielle de son énergie cinétique, déterminée par un facteur défini par l'utilisateur 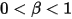 :
:
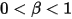 :
:◦ Translation
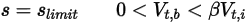
Equation 2.451
◦ Rotation
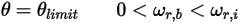
Equation 2.452
• Rebond parfait : modèle qui détermine que, lorsqu'un corps solide ou une frontière atteint la limite de son mouvement, il/elle change de direction sans perte de son énergie cinétique 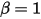 :
:
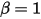 :
:◦ Translation

Equation 2.453
◦ Rotation

Equation 2.454