Modélisation du transfert de chaleur par rayonnement
Dans un système de fluide thermique, les surfaces solides ou l'écoulement de fluides (ou les deux) peuvent être soumis à un réchauffement ou un refroidissement causé par un rayonnement. Dans des modèles CFA, le transfert de chaleur par rayonnement est expliqué par la résolution de l'équation de transfert radiatif, puis par l'obtention du terme source de rayonnement pour l'équation de conservation d'énergie totale. Une approche de modélisation largement utilisée, le modèle de rayonnement de surface à surface (S2S) est le modèle choisi dans Creo Flow Analysis.
Equation de transfert radiatif
Un rayonnement traversant une couche d'un milieu absorbant, d'émission et dispersif dans une direction donnée, le rayon perd de l'énergie par absorption et dispersion du rayon. Le rayon gagne également de l'énergie des sources de lumière dans le milieu par émission et la diffusion dirigée vers le rayon. L'équilibre énergétique global du rayon sur une couche infinie du milieu produit une équation différentielle, connue sous le nom d'équation de transfert radiatif.
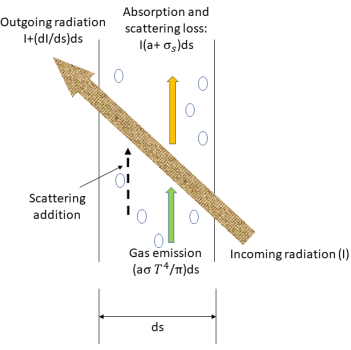
Pour dériver l'équation de transfert radiatif, considérez un rayonnement entrant avec une intensité de I qui traverse un milieu, par exemple, un gaz, avec l'épaisseur incrémentale ds dans la direction de 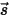 , comme illustré à la figure. A travers le milieu considéré, l'incidence à l'emplacement
, comme illustré à la figure. A travers le milieu considéré, l'incidence à l'emplacement 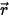 ⃗ et pour la direction
⃗ et pour la direction 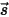 change de quatre manières, augmentant (gain d'énergie +) ou diminuant (perte d'énergie -) l'intensité du rayonnement
change de quatre manières, augmentant (gain d'énergie +) ou diminuant (perte d'énergie -) l'intensité du rayonnement 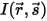 :
:
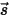 , comme illustré à la figure. A travers le milieu considéré, l'incidence à l'emplacement
, comme illustré à la figure. A travers le milieu considéré, l'incidence à l'emplacement 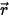 ⃗ et pour la direction
⃗ et pour la direction 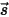 change de quatre manières, augmentant (gain d'énergie +) ou diminuant (perte d'énergie -) l'intensité du rayonnement
change de quatre manières, augmentant (gain d'énergie +) ou diminuant (perte d'énergie -) l'intensité du rayonnement 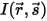 :
:• Absorption : milieu, par exemple un gaz, qui absorbe une fraction du rayonnement qui le traverse. Avec le coefficient d'absorption 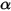 , l'énergie de rayonnement perdue par absorption est :
, l'énergie de rayonnement perdue par absorption est :
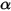 , l'énergie de rayonnement perdue par absorption est :
, l'énergie de rayonnement perdue par absorption est :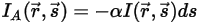
équation 2.282
• Dispersion : milieu, par exemple un gaz, qui disperse une fraction de l'énergie de rayonnement dans une autre direction (loin de la direction 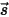 ) lorsque le rayonnement traverse le milieu. Avec le coefficient de dispersion
) lorsque le rayonnement traverse le milieu. Avec le coefficient de dispersion 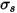 , l'énergie de rayonnement perdue par dispersion est :
, l'énergie de rayonnement perdue par dispersion est :
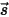 ) lorsque le rayonnement traverse le milieu. Avec le coefficient de dispersion
) lorsque le rayonnement traverse le milieu. Avec le coefficient de dispersion 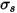 , l'énergie de rayonnement perdue par dispersion est :
, l'énergie de rayonnement perdue par dispersion est :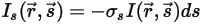
Equation 2.283
• Emission : un milieu émet une énergie de rayonnement vers le rayon sous la forme d'un corps gris en fonction de ses caractéristiques locales de température (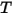 ) et d'émission. Selon la loi de Stefan-Boltzmann et la réciprocité entre l'émission et l'absorption (équation 2.274 et équation 2.279), le rayonnement émis par le milieu est :
) et d'émission. Selon la loi de Stefan-Boltzmann et la réciprocité entre l'émission et l'absorption (équation 2.274 et équation 2.279), le rayonnement émis par le milieu est : 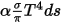 .
.
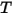 ) et d'émission. Selon la loi de Stefan-Boltzmann et la réciprocité entre l'émission et l'absorption (équation 2.274 et équation 2.279), le rayonnement émis par le milieu est :
) et d'émission. Selon la loi de Stefan-Boltzmann et la réciprocité entre l'émission et l'absorption (équation 2.274 et équation 2.279), le rayonnement émis par le milieu est : 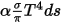 .
.En outre, en supposant que n est l'indice de réfraction du milieu (résultat du rapport entre la vitesse de la lumière dans le vide et la vitesse de la lumière dans le milieu indiqué), l'énergie réelle acquise par le rayonnement est :
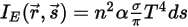
Equation 2.284
• Dispersion d'autres rayonnements : une fraction d'autres sources de rayonnement dans la couche du milieu est dispersée dans le rayonnement en fonction des vecteurs de position et de direction 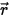 et
et 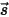 . En introduisant
. En introduisant 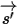
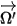 pour représenter la direction et l'angle solide du faisceau de rayonnement et
pour représenter la direction et l'angle solide du faisceau de rayonnement et 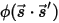 pour représenter la fonction de phase, vous disposez de la fraction d'intensité d'un rayon qui se déplace dans toutes les directions pour être dispersé dans la direction de
pour représenter la fonction de phase, vous disposez de la fraction d'intensité d'un rayon qui se déplace dans toutes les directions pour être dispersé dans la direction de 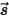 ⃗ :
⃗ :
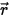 et
et 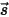 . En introduisant
. En introduisant 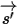
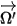 pour représenter la direction et l'angle solide du faisceau de rayonnement et
pour représenter la direction et l'angle solide du faisceau de rayonnement et 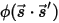 pour représenter la fonction de phase, vous disposez de la fraction d'intensité d'un rayon qui se déplace dans toutes les directions pour être dispersé dans la direction de
pour représenter la fonction de phase, vous disposez de la fraction d'intensité d'un rayon qui se déplace dans toutes les directions pour être dispersé dans la direction de 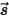 ⃗ :
⃗ :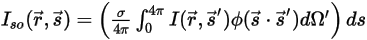
équation 2.285
Notez que dans l'équation 2.285, les processus de dispersion sont ignorés.
Avec le rayonnement entrant 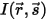 et le rayonnement sortant
et le rayonnement sortant 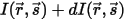 , l'équilibre de l'énergie de rayonnement dans la direction
, l'équilibre de l'énergie de rayonnement dans la direction 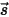 ⃗ prend la forme suivante :
⃗ prend la forme suivante :
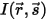 et le rayonnement sortant
et le rayonnement sortant 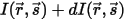 , l'équilibre de l'énergie de rayonnement dans la direction
, l'équilibre de l'énergie de rayonnement dans la direction 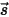 ⃗ prend la forme suivante :
⃗ prend la forme suivante :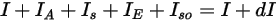
équation 2.286
En remplaçant l'équation 2.282 par l'équation 2.285 dans l'équation 2.286, puis en la divisant par 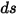 , vous obtenez l'équation de transfert radiatif suivante :
, vous obtenez l'équation de transfert radiatif suivante :
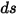 , vous obtenez l'équation de transfert radiatif suivante :
, vous obtenez l'équation de transfert radiatif suivante :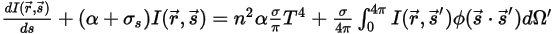
équation 2.287
L'équation de transfert radiatif est une équation intégro-différentielle du premier ordre pour l'intensité de rayonnement 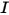 dans une direction fixe
dans une direction fixe 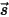 . Pour résoudre cette équation au sein d'un domaine, vous devez disposer du champ de température du domaine, des conditions aux limites pour
. Pour résoudre cette équation au sein d'un domaine, vous devez disposer du champ de température du domaine, des conditions aux limites pour 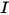 sur les surfaces internes et externes, ainsi que les interfaces entre deux milieux différents.
sur les surfaces internes et externes, ainsi que les interfaces entre deux milieux différents.
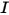 dans une direction fixe
dans une direction fixe 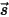 . Pour résoudre cette équation au sein d'un domaine, vous devez disposer du champ de température du domaine, des conditions aux limites pour
. Pour résoudre cette équation au sein d'un domaine, vous devez disposer du champ de température du domaine, des conditions aux limites pour 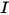 sur les surfaces internes et externes, ainsi que les interfaces entre deux milieux différents.
sur les surfaces internes et externes, ainsi que les interfaces entre deux milieux différents.La température locale du milieu est obtenue en résolvant l'équation de conservation d'énergie totale (y compris les sources de rayonnement), décrite dans le module Chaleur (Heat). Toutefois, pour le rayonnement thermique, le traitement aux limites est complexe et dépend des modèles de rayonnement. En général, une limite peut être un milieu opaque qui émet, réfléchit et absorbe, ou bien un milieu semi-transparent qui transmet également. La réflexion et la transmission peuvent être diffuses ou spéculaires, ou à la fois diffuses et spéculaires. Par exemple, sur une frontière opaque d'émission et réfléchissante avec un rayonnement gris, et en fonction du type de réflexion, l'intensité d'un rayon peut être exprimée comme suit :
◦ Frontière opaque avec émission et réflexion diffuses :
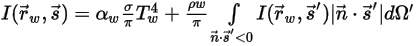
Equation 2.288
◦ Frontière opaque avec émission diffuse et réflexion spéculaire :
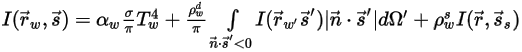
Equation 2.289
où,
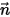 ⃗ ⃗ | vecteur normal unitaire à la position 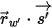 |
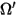 | direction et angle solide d'un rayon réfléchi de façon diffuse (réflexion uniforme dans toutes les directions) |
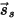 | direction d'un rayon réfléchi de façon spéculaire (réflexion parfaite en fonction de l'incidence) |
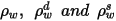 | réflectivité de la surface, réflectivité diffuse et réflectivité spéculaire, qui présentent respectivement la relation suivante : 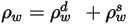 équation 2.290 |
Avec les conditions aux limites données, l'équation 2.287 régit le transfert de l'intensité du rayonnement dans une direction spécifiée. Pour les rayonnements gris, l'équation 2.287 doit être résolue dans toutes les directions différentes dans une sphère. Pour les rayonnements non gris, l'intensité dépend également des longueurs d'onde. Par conséquent, elle doit être résolue dans toutes les directions sur l'ensemble du spectre des longueurs d'onde. Clairement, la solution directe de l'équation de transfert radiatif est très chronophage. Dans de nombreuses simulations d'ingénierie, il est donc souhaitable d'utiliser des modèles simplifiés mais approximatifs pour tenir compte des dépendances directionnelles et spectrales. Dans les simulations CFD, les modèles de rayonnement suivants sont régulièrement adoptés. Une description détaillée peut être consultée dans les références.
Références : R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modèle de rayonnement Rosseland
Références : R, Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modèle de rayonnement P-1
Références : R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modèle de rayonnement par transfert discret
Références : N. G. Shah, "A New Method of Computation of Radiant Heat Transfer in Combustion Chambers", PhD thesis, Imperial College of Science and Technology, London, England, 1979.
Références : M. G. Carvalho, T. Farias, and P. Fontes, "Predicting Radiative Heat Transfer in Absorbing, Emitting, and Scattering Media Using the Discrete Transfer Method", In W. A. Fiveland et al., editor, "Fundamentals of Radiation Heat Transfer", volume 160, pages 17-26. ASME HTD, 1991.
▪ Modèle de rayonnement de surface à surface (S2S)
Références : R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
▪ Modèle de rayonnement basé sur des ordonnées discrètes
Références : G. D. Raithby and E. H. Chui, "A Finite-Volume Method for Predicting a Radiant Heat Transfer in Enclosures with Participating Media", J. Heat Transfer, 112:415-423, 1990.
Références : E. H. Chui and G. D. Raithby, "Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method", Numerical Heat Transfer, Part B, 23:269-288, 1993.
Chaque modèle possède ses propres avantages et limites en matière de précision et de coûts. Par exemple, si le modèle Rosseland ne résout pas une équation de transfert pour le rayonnement incident, il s'agit du modèle de rayonnement le plus rapide qui nécessite le moins de mémoire supplémentaire. Rosseland ne peut être utilisé que pour des milieux optiquement épais (l'épaisseur optique est le logarithme naturel du rapport entre la puissance rayonnante incidente et la puissance rayonnante transmise dans un milieu) en raison de la simplification excessive de l'équation de transfert radiatif.
Le modèle de rayonnement basé sur des ordonnées discrètes (DO) transforme l'équation 2.287 en une équation de transfert pour l'intensité de rayonnement dans les coordonnées spatiales 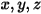 et la résout sur un nombre fini d'angles solides discrets associés à l'orientation du vecteur
et la résout sur un nombre fini d'angles solides discrets associés à l'orientation du vecteur 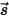 . Le nombre d'angles solides sélectionnés détermine directement la précision et le coût de calcul. L'approche de modélisation DO est également identique à l'approche utilisée pour les équations d'écoulement de fluide et d'énergie. Actuellement, il s'agit du modèle de rayonnement le plus général qui couvre l'ensemble des épaisseurs optiques. Il peut être appliqué aux problèmes allant du rayonnement de surface à surface à un rayonnement dans un milieu participatif, tel qu'un système de combustion. Toutefois, le coût de calcul du modèle DO est élevé pour les rayonnements non gris.
. Le nombre d'angles solides sélectionnés détermine directement la précision et le coût de calcul. L'approche de modélisation DO est également identique à l'approche utilisée pour les équations d'écoulement de fluide et d'énergie. Actuellement, il s'agit du modèle de rayonnement le plus général qui couvre l'ensemble des épaisseurs optiques. Il peut être appliqué aux problèmes allant du rayonnement de surface à surface à un rayonnement dans un milieu participatif, tel qu'un système de combustion. Toutefois, le coût de calcul du modèle DO est élevé pour les rayonnements non gris.
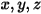 et la résout sur un nombre fini d'angles solides discrets associés à l'orientation du vecteur
et la résout sur un nombre fini d'angles solides discrets associés à l'orientation du vecteur 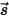 . Le nombre d'angles solides sélectionnés détermine directement la précision et le coût de calcul. L'approche de modélisation DO est également identique à l'approche utilisée pour les équations d'écoulement de fluide et d'énergie. Actuellement, il s'agit du modèle de rayonnement le plus général qui couvre l'ensemble des épaisseurs optiques. Il peut être appliqué aux problèmes allant du rayonnement de surface à surface à un rayonnement dans un milieu participatif, tel qu'un système de combustion. Toutefois, le coût de calcul du modèle DO est élevé pour les rayonnements non gris.
. Le nombre d'angles solides sélectionnés détermine directement la précision et le coût de calcul. L'approche de modélisation DO est également identique à l'approche utilisée pour les équations d'écoulement de fluide et d'énergie. Actuellement, il s'agit du modèle de rayonnement le plus général qui couvre l'ensemble des épaisseurs optiques. Il peut être appliqué aux problèmes allant du rayonnement de surface à surface à un rayonnement dans un milieu participatif, tel qu'un système de combustion. Toutefois, le coût de calcul du modèle DO est élevé pour les rayonnements non gris.Parmi les modèles de rayonnement susmentionnés, le modèle de surface à surface (S2S) est particulièrement adapté pour modéliser le transfert radiatif dans une enceinte sans tenir compte du milieu participatif. Parmi les exemples classiques, on compte les appareils de chauffage radiant et les systèmes ainsi que les systèmes de compartiment moteur et de soubassement de carrosserie. Dans ce cas, les modèles de rayonnement destinés au rayonnement dans un milieu participatif manquent parfois d'efficacité. Par rapport au modèle de rayonnement DO, le modèle S2S a un temps par itération plus rapide, bien que le calcul du facteur de forme puisse nécessiter une utilisation importante du processeur. Dans Creo Flow Analysis, le choix actuel du modèle pour le transfert de chaleur par rayonnement est le modèle de rayonnement S2S.
Modèle de rayonnement de surface à surface (S2S)
Le modèle de rayonnement de surface à surface explique le transfert radiatif dans une enceinte de surfaces grises diffusantes sans milieu participatif. L'échange de l'énergie de rayonnement de surface à surface dépend de deux facteurs principaux : les caractéristiques de rayonnement des surfaces impliquées et les paramètres géométriques, y compris la superficie et la forme des surfaces, ainsi que la position relative de l'une par rapport à l'autre (orientation et distance de séparation). Dans le modèle de rayonnement S2S, le transfert de chaleur par rayonnement entre surfaces est pris en compte par le modèle de rayonnement gris diffusant, tandis que les paramètres géométriques sont pris en compte par une fonction géométrique appelée facteur de forme.
• Rayonnement gris diffusant
Le modèle de rayonnement S2S part du principe que les surfaces sont grises et diffuses (rayonnement gris). Pour une surface grise, l'émissivité 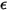 et l'absorptivité
et l'absorptivité 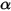 des surfaces sont indépendantes de la longueur d'onde des rayons sortants et entrants. Selon la loi du rayonnement de Kirchhoff dans l'équation 2.274, l'émissivité est égale à l'absorptivité :
des surfaces sont indépendantes de la longueur d'onde des rayons sortants et entrants. Selon la loi du rayonnement de Kirchhoff dans l'équation 2.274, l'émissivité est égale à l'absorptivité :
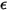 et l'absorptivité
et l'absorptivité 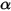 des surfaces sont indépendantes de la longueur d'onde des rayons sortants et entrants. Selon la loi du rayonnement de Kirchhoff dans l'équation 2.274, l'émissivité est égale à l'absorptivité :
des surfaces sont indépendantes de la longueur d'onde des rayons sortants et entrants. Selon la loi du rayonnement de Kirchhoff dans l'équation 2.274, l'émissivité est égale à l'absorptivité :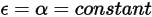
Equation 2.291
En outre, avec l'hypothèse d'une surface diffuse, aucune réflexion spéculaire ne se produit sur la surface et la réflectivité (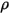 ) du rayonnement incident sur la surface est isotrope par rapport à l'angle solide. Dans l'équation 2.290, la réflectivité de la surface est déterminée comme suit :
) du rayonnement incident sur la surface est isotrope par rapport à l'angle solide. Dans l'équation 2.290, la réflectivité de la surface est déterminée comme suit :
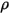 ) du rayonnement incident sur la surface est isotrope par rapport à l'angle solide. Dans l'équation 2.290, la réflectivité de la surface est déterminée comme suit :
) du rayonnement incident sur la surface est isotrope par rapport à l'angle solide. Dans l'équation 2.290, la réflectivité de la surface est déterminée comme suit :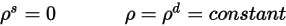
Equation 2.292
où,
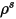 | réflexion spéculaire de la surface |
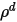 | réflectivité diffuse |
Pour une surface non opaque ou semi-transparente, la transmissivité 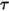 est également indépendante des longueurs d'onde :
est également indépendante des longueurs d'onde :
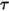 est également indépendante des longueurs d'onde :
est également indépendante des longueurs d'onde :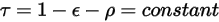
Equation 2.293
Le modèle de surface à surface grise diffusante suppose que l'échange d'énergie de rayonnement entre les surfaces n'est pratiquement pas affecté par le milieu qui les sépare. Ainsi, si une certaine quantité d'énergie rayonnante 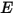 est incidente sur une surface par unité de surface (irradiance), les portions de l'énergie de rayonnement réfléchie, absorbée et transmise sont
est incidente sur une surface par unité de surface (irradiance), les portions de l'énergie de rayonnement réfléchie, absorbée et transmise sont 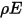 ,
, 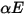 et
et 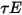 respectivement. Etant donné que, pour la plupart des applications, les surfaces sont opaques au rayonnement thermique dans le spectre infrarouge, les surfaces de rayonnement peuvent être considérées comme opaques. La transmissivité peut donc être ignorée
respectivement. Etant donné que, pour la plupart des applications, les surfaces sont opaques au rayonnement thermique dans le spectre infrarouge, les surfaces de rayonnement peuvent être considérées comme opaques. La transmissivité peut donc être ignorée 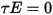 . Dans l'équation 2.273 et l'équation 2.274, la réflectivité de la surface
. Dans l'équation 2.273 et l'équation 2.274, la réflectivité de la surface 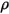 est exprimée comme suit :
est exprimée comme suit :
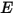 est incidente sur une surface par unité de surface (irradiance), les portions de l'énergie de rayonnement réfléchie, absorbée et transmise sont
est incidente sur une surface par unité de surface (irradiance), les portions de l'énergie de rayonnement réfléchie, absorbée et transmise sont 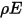 ,
, 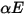 et
et 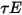 respectivement. Etant donné que, pour la plupart des applications, les surfaces sont opaques au rayonnement thermique dans le spectre infrarouge, les surfaces de rayonnement peuvent être considérées comme opaques. La transmissivité peut donc être ignorée
respectivement. Etant donné que, pour la plupart des applications, les surfaces sont opaques au rayonnement thermique dans le spectre infrarouge, les surfaces de rayonnement peuvent être considérées comme opaques. La transmissivité peut donc être ignorée 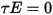 . Dans l'équation 2.273 et l'équation 2.274, la réflectivité de la surface
. Dans l'équation 2.273 et l'équation 2.274, la réflectivité de la surface 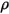 est exprimée comme suit :
est exprimée comme suit :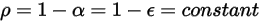
Equation 2.294
avec les hypothèses du rayonnement gris diffusant, l'équation de modélisation S2S est construite en fonction de la conservation d'énergie sur chaque surface.
• Equation de modélisation S2S
L'hypothèse principale du modèle S2S est que dans un système fermé, le transfert de chaleur par rayonnement ne se produit qu'entre des surfaces grises diffusantes (rayonnement gris). Vous pouvez ignorer l'absorption, l'émission ou la diffusion du rayonnement dans le milieu séparant les surfaces. Par conséquent, seul le rayonnement de surface à surface est pris en considération pour l'analyse numérique.
Le flux d'énergie de rayonnement qui quitte une surface donnée se compose d'énergie directement émise et réfléchie. Le flux d'énergie réfléchi dépend du flux d'énergie incident de l'environnement, qui peut ensuite être exprimé en termes de flux d'énergie quittant toutes les autres surfaces. Pour calculer le flux d'énergie de rayonnement net dans une surface, il convient de définir la radiosité 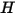 , qui correspond à la somme du rayonnement émis par unité de surface (émittance)
, qui correspond à la somme du rayonnement émis par unité de surface (émittance) 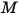 et d'une partie de la puissance de rayonnement réfléchie reçue par la surface par unité de surface (irradiance)
et d'une partie de la puissance de rayonnement réfléchie reçue par la surface par unité de surface (irradiance) 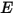 :
:
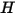 , qui correspond à la somme du rayonnement émis par unité de surface (émittance)
, qui correspond à la somme du rayonnement émis par unité de surface (émittance) 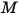 et d'une partie de la puissance de rayonnement réfléchie reçue par la surface par unité de surface (irradiance)
et d'une partie de la puissance de rayonnement réfléchie reçue par la surface par unité de surface (irradiance) 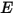 :
: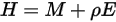
Equation 2.295
Pour une surface opaque 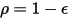 , vous avez la radiosité :
, vous avez la radiosité :
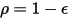 , vous avez la radiosité :
, vous avez la radiosité :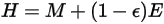
équation 2.296
avec les hypothèses du modèle S2S, il est possible de formuler le système d'équations linéaires suivant pour calculer la radiosité sur chaque surface d'un système fermé. En supposant que 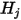 représente la radiosité sur une surface arbitraire
représente la radiosité sur une surface arbitraire 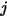 ,
, 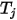 la température de la surface et
la température de la surface et 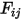 le facteur de forme entre les surfaces
le facteur de forme entre les surfaces 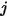 et
et  , vous obtenez la radiosité de la surface
, vous obtenez la radiosité de la surface  :
:
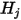 représente la radiosité sur une surface arbitraire
représente la radiosité sur une surface arbitraire 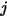 ,
, 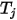 la température de la surface et
la température de la surface et 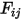 le facteur de forme entre les surfaces
le facteur de forme entre les surfaces 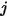 et
et  , vous obtenez la radiosité de la surface
, vous obtenez la radiosité de la surface  :
: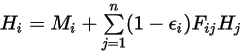
équation 2.297
où 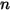 correspond au nombre de surfaces participant au transfert de chaleur par rayonnement. En introduisant le symbole de Kronecker
correspond au nombre de surfaces participant au transfert de chaleur par rayonnement. En introduisant le symbole de Kronecker 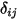 et en appliquant la loi de Stefan-Boltzmann pour le rayonnement gris, l'équation 2.278, vous pouvez réécrire l'équation 2.297 et dériver l'équation de modélisation S2S :
et en appliquant la loi de Stefan-Boltzmann pour le rayonnement gris, l'équation 2.278, vous pouvez réécrire l'équation 2.297 et dériver l'équation de modélisation S2S :
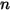 correspond au nombre de surfaces participant au transfert de chaleur par rayonnement. En introduisant le symbole de Kronecker
correspond au nombre de surfaces participant au transfert de chaleur par rayonnement. En introduisant le symbole de Kronecker 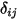 et en appliquant la loi de Stefan-Boltzmann pour le rayonnement gris, l'équation 2.278, vous pouvez réécrire l'équation 2.297 et dériver l'équation de modélisation S2S :
et en appliquant la loi de Stefan-Boltzmann pour le rayonnement gris, l'équation 2.278, vous pouvez réécrire l'équation 2.297 et dériver l'équation de modélisation S2S :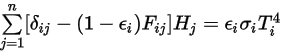
équation 2.298
Avec le facteur de forme pré-calculé 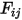 , le système d'équations 2.298 linéaires est résolu pour obtenir
, le système d'équations 2.298 linéaires est résolu pour obtenir 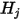 pour les surfaces participatives. Les flux de rayonnement thermique nets sur chaque surface sont ainsi calculés facilement. Pour la surface
pour les surfaces participatives. Les flux de rayonnement thermique nets sur chaque surface sont ainsi calculés facilement. Pour la surface  , le flux de rayonnement thermique net
, le flux de rayonnement thermique net 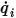 correspond à la différence entre le rayonnement sortant (
correspond à la différence entre le rayonnement sortant (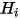 ) et le rayonnement entrant (
) et le rayonnement entrant (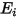 ) par unité de surface. Dans l'équation 2.278 et l'équation 2.296, vous pouvez dériver la formulation de flux suivante :
) par unité de surface. Dans l'équation 2.278 et l'équation 2.296, vous pouvez dériver la formulation de flux suivante :
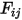 , le système d'équations 2.298 linéaires est résolu pour obtenir
, le système d'équations 2.298 linéaires est résolu pour obtenir 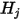 pour les surfaces participatives. Les flux de rayonnement thermique nets sur chaque surface sont ainsi calculés facilement. Pour la surface
pour les surfaces participatives. Les flux de rayonnement thermique nets sur chaque surface sont ainsi calculés facilement. Pour la surface  , le flux de rayonnement thermique net
, le flux de rayonnement thermique net 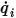 correspond à la différence entre le rayonnement sortant (
correspond à la différence entre le rayonnement sortant (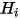 ) et le rayonnement entrant (
) et le rayonnement entrant (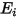 ) par unité de surface. Dans l'équation 2.278 et l'équation 2.296, vous pouvez dériver la formulation de flux suivante :
) par unité de surface. Dans l'équation 2.278 et l'équation 2.296, vous pouvez dériver la formulation de flux suivante :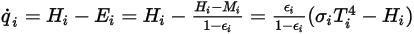
Equation 2.299
Pour une superficie donnée 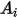 , les flux de rayonnement thermique nets quittant la surface
, les flux de rayonnement thermique nets quittant la surface 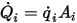 sont calculés comme suit :
sont calculés comme suit :
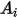 , les flux de rayonnement thermique nets quittant la surface
, les flux de rayonnement thermique nets quittant la surface 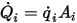 sont calculés comme suit :
sont calculés comme suit :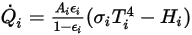
Equation 2.300
Le modèle S2S est composé d'un système d'équations linéaires sous la forme de l'équation 2.298. L'avantage de l'application du modèle est que, pour les facteurs de forme et les températures donnés, vous calculez les flux thermiques nets en résolvant un système d'équations linéaires, qui sont calculées par l'application d'algorithmes numériques. Toutefois, l'application du modèle de surface à surface proposé présente une difficulté : le calcul des facteurs de forme 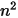 pour un nombre n de surfaces participatives. Cela peut prendre beaucoup de temps, en particulier lorsque le nombre de surfaces augmente.
pour un nombre n de surfaces participatives. Cela peut prendre beaucoup de temps, en particulier lorsque le nombre de surfaces augmente.
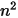 pour un nombre n de surfaces participatives. Cela peut prendre beaucoup de temps, en particulier lorsque le nombre de surfaces augmente.
pour un nombre n de surfaces participatives. Cela peut prendre beaucoup de temps, en particulier lorsque le nombre de surfaces augmente.Calcul du facteur de forme
Dans l'équation 2.298 de la modélisation S2S, le facteur de forme 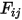 correspond à la proportion de rayonnement quittant la surface
correspond à la proportion de rayonnement quittant la surface  et frappant la surface
et frappant la surface 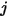 . Comme illustré dans la figure 2.37, en supposant que
. Comme illustré dans la figure 2.37, en supposant que 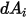 correspond à la zone différentielle sur la surface
correspond à la zone différentielle sur la surface  et
et 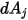 à la zone différentielle sur la surface
à la zone différentielle sur la surface 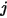 et que la distance entre
et que la distance entre 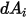 et
et 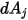 est
est 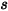 , vous exprimez le facteur de forme
, vous exprimez le facteur de forme 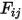 de
de 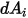 dans
dans 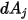 à une distance
à une distance 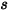 comme suit :
comme suit :
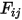 correspond à la proportion de rayonnement quittant la surface
correspond à la proportion de rayonnement quittant la surface  et frappant la surface
et frappant la surface 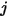 . Comme illustré dans la figure 2.37, en supposant que
. Comme illustré dans la figure 2.37, en supposant que 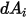 correspond à la zone différentielle sur la surface
correspond à la zone différentielle sur la surface  et
et 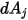 à la zone différentielle sur la surface
à la zone différentielle sur la surface 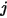 et que la distance entre
et que la distance entre 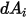 et
et 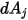 est
est 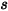 , vous exprimez le facteur de forme
, vous exprimez le facteur de forme 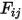 de
de 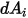 dans
dans 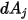 à une distance
à une distance 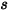 comme suit :
comme suit :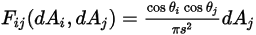
Equation 2.301
où 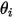 et
et 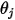 correspondent à l'angle entre les directions normales à la surface et un rayon entre les deux zones différentielles.
correspondent à l'angle entre les directions normales à la surface et un rayon entre les deux zones différentielles.
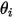 et
et 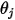 correspondent à l'angle entre les directions normales à la surface et un rayon entre les deux zones différentielles.
correspondent à l'angle entre les directions normales à la surface et un rayon entre les deux zones différentielles.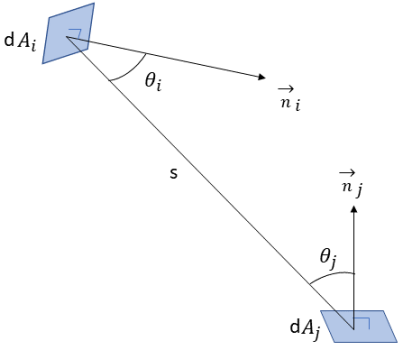
Figure 2.37
Si 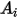 et
et 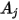 sont les superficies données
sont les superficies données  et
et 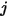 , respectivement, le facteur de forme de la surface
, respectivement, le facteur de forme de la surface  à la surface
à la surface 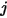 correspond à l'intégrale de surface moyenne de l'équation 2.301 sur les surfaces
correspond à l'intégrale de surface moyenne de l'équation 2.301 sur les surfaces  et
et 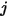 :
:
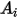 et
et 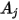 sont les superficies données
sont les superficies données  et
et 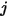 , respectivement, le facteur de forme de la surface
, respectivement, le facteur de forme de la surface  à la surface
à la surface 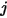 correspond à l'intégrale de surface moyenne de l'équation 2.301 sur les surfaces
correspond à l'intégrale de surface moyenne de l'équation 2.301 sur les surfaces  et
et 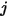 :
: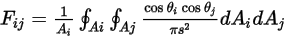
Equation 2.302
Notez que le rayonnement de surface à surface ne se produit que lorsque les deux surfaces sont visibles l'une par rapport à l'autre ou que le facteur de forme est différent de zéro. En introduisant le symbole de Kronecker 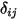 par rapport à la visibilité entre
par rapport à la visibilité entre 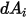 et
et 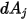 :
:
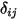 par rapport à la visibilité entre
par rapport à la visibilité entre 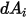 et
et 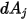 :
: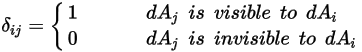
Equation 2.303
vous pouvez réécrire l'équation 2.302 comme suit :
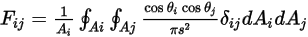
Equation 2.304
Pour deux surfaces visibles l'une par rapport à l'autre, une surface donnée  ne diffuse qu'une partie de l'énergie de rayonnement sortant vers la surface
ne diffuse qu'une partie de l'énergie de rayonnement sortant vers la surface 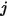 , comme illustré dans la figure 2.378. Par conséquent, le facteur de forme adimensionnel
, comme illustré dans la figure 2.378. Par conséquent, le facteur de forme adimensionnel 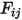 représente la partie de l'énergie qui quitte la surface
représente la partie de l'énergie qui quitte la surface  et atteint la surface
et atteint la surface 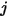 . Les caractéristiques sont répertoriées dans la liste ci-après :
. Les caractéristiques sont répertoriées dans la liste ci-après :
 ne diffuse qu'une partie de l'énergie de rayonnement sortant vers la surface
ne diffuse qu'une partie de l'énergie de rayonnement sortant vers la surface 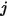 , comme illustré dans la figure 2.378. Par conséquent, le facteur de forme adimensionnel
, comme illustré dans la figure 2.378. Par conséquent, le facteur de forme adimensionnel 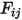 représente la partie de l'énergie qui quitte la surface
représente la partie de l'énergie qui quitte la surface  et atteint la surface
et atteint la surface 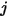 . Les caractéristiques sont répertoriées dans la liste ci-après :
. Les caractéristiques sont répertoriées dans la liste ci-après :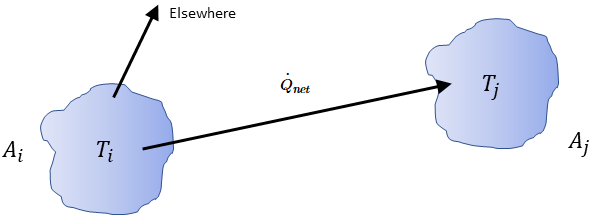
Figure 2.378
• Somme de facteurs de forme : le rayonnement quittant une surface étant conservé, la somme de tous les facteurs de forme d'une surface donnée  est une unité. Pour un système fermé par des surfaces
est une unité. Pour un système fermé par des surfaces 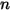 , vous utilisez
, vous utilisez
 est une unité. Pour un système fermé par des surfaces
est une unité. Pour un système fermé par des surfaces 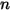 , vous utilisez
, vous utilisez
Equation 2.305
• Surfaces visibles par elles-mêmes : le rayonnement se déplaçant en ligne droite, aucun rayon provenant d'une surface convexe ne peut quitter la surface, puis frapper la même surface ultérieurement. Par conséquent, les surfaces convexes ne peuvent pas être considérées comme visibles par elles-mêmes :
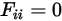
Equation 2.306
Pour les surfaces concaves, le rayon sortant d'une position sur la surface peut toucher la même surface ultérieurement à une autre position. Par conséquent, une surface concave peut être visible par elle-même :
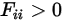
Equation 2.307
• Superposition : pour un système de surfaces 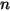 , si une surface donnée
, si une surface donnée  émet un rayonnement vers un nombre
émet un rayonnement vers un nombre 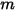 de surfaces (
de surfaces (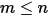 ), le facteur de forme entre la surface
), le facteur de forme entre la surface  et le nombre
et le nombre 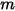 de surfaces est égal à la somme des facteurs de forme entre la surface
de surfaces est égal à la somme des facteurs de forme entre la surface  et chaque surface du nombre
et chaque surface du nombre 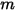 de surfaces :
de surfaces :
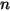 , si une surface donnée
, si une surface donnée  émet un rayonnement vers un nombre
émet un rayonnement vers un nombre 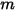 de surfaces (
de surfaces (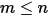 ), le facteur de forme entre la surface
), le facteur de forme entre la surface  et le nombre
et le nombre 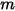 de surfaces est égal à la somme des facteurs de forme entre la surface
de surfaces est égal à la somme des facteurs de forme entre la surface  et chaque surface du nombre
et chaque surface du nombre 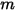 de surfaces :
de surfaces :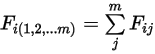
Equation 2.308
La règle de superposition ou la règle de somme est utile lorsqu'une géométrie n'est pas disponible avec les graphiques ou les graphes donnés. Elle vous permet d'exprimer la géométrie recherchée à l'aide de la somme ou de la différence des géométries connues.
• Réciprocité : l'équation 2.304 définit le facteur de forme 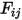 comme la fraction de l'énergie de rayonnement qui quitte la surface
comme la fraction de l'énergie de rayonnement qui quitte la surface  et atteint la surface
et atteint la surface 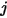 . De même, le facteur de forme
. De même, le facteur de forme 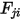 , qui correspond à la partie de l'énergie qui quitte la surface
, qui correspond à la partie de l'énergie qui quitte la surface 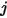 et qui atteint la surface
et qui atteint la surface  , est exprimé comme suit :
, est exprimé comme suit :
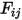 comme la fraction de l'énergie de rayonnement qui quitte la surface
comme la fraction de l'énergie de rayonnement qui quitte la surface  et atteint la surface
et atteint la surface 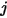 . De même, le facteur de forme
. De même, le facteur de forme 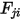 , qui correspond à la partie de l'énergie qui quitte la surface
, qui correspond à la partie de l'énergie qui quitte la surface 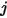 et qui atteint la surface
et qui atteint la surface  , est exprimé comme suit :
, est exprimé comme suit :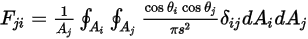
Equation 2.309
Si vous comparez l'équation 2.309 à l'équation 2.304, vous obtenez la relation suivante :
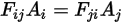
Equation 2.310
L'équation 2.310 est décrite comme la réciprocité des facteurs de forme. Avec ce théorème de réciprocité, vous pouvez calculer directement une seule des paires de facteurs de forme.
Clustering
Le modèle de rayonnement S2S nécessite de nombreuses ressources de calcul lorsque le nombre de surfaces de rayonnement est important. Pour réduire la durée de calcul et les besoins de stockage, vous pouvez réduire le nombre de surfaces de rayonnement en regroupant plusieurs faces adjacentes de cellules frontières afin de créer des clusters de surfaces. La radiosité (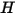 ) est ensuite calculée pour les clusters de surfaces. Ces valeurs sont ensuite distribuées aux faces de cellules frontières au sein de chaque cluster pour calculer les températures de paroi. Etant donné que les termes source de rayonnement ne sont pas linéaires (proportionnels à la quatrième puissance de température), assurez-vous de calculer la température moyenne des clusters de surfaces et de distribuer le flux et les termes source de manière appropriée parmi les faces frontières qui forment les clusters.
) est ensuite calculée pour les clusters de surfaces. Ces valeurs sont ensuite distribuées aux faces de cellules frontières au sein de chaque cluster pour calculer les températures de paroi. Etant donné que les termes source de rayonnement ne sont pas linéaires (proportionnels à la quatrième puissance de température), assurez-vous de calculer la température moyenne des clusters de surfaces et de distribuer le flux et les termes source de manière appropriée parmi les faces frontières qui forment les clusters.
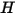 ) est ensuite calculée pour les clusters de surfaces. Ces valeurs sont ensuite distribuées aux faces de cellules frontières au sein de chaque cluster pour calculer les températures de paroi. Etant donné que les termes source de rayonnement ne sont pas linéaires (proportionnels à la quatrième puissance de température), assurez-vous de calculer la température moyenne des clusters de surfaces et de distribuer le flux et les termes source de manière appropriée parmi les faces frontières qui forment les clusters.
) est ensuite calculée pour les clusters de surfaces. Ces valeurs sont ensuite distribuées aux faces de cellules frontières au sein de chaque cluster pour calculer les températures de paroi. Etant donné que les termes source de rayonnement ne sont pas linéaires (proportionnels à la quatrième puissance de température), assurez-vous de calculer la température moyenne des clusters de surfaces et de distribuer le flux et les termes source de manière appropriée parmi les faces frontières qui forment les clusters.La température des clusters de surfaces est obtenue en réalisant une moyenne de la température des faces frontières, comme illustré dans l'équation suivante :
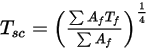
Equation 2.311
où 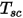 correspond à la température du cluster de surfaces, et
correspond à la température du cluster de surfaces, et 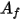 et
et 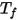 à la surface et à la température de la face de la cellule frontière dans les simulations CFA. La somme est effectuée sur toutes les faces d'un cluster de surfaces.
à la surface et à la température de la face de la cellule frontière dans les simulations CFA. La somme est effectuée sur toutes les faces d'un cluster de surfaces.
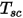 correspond à la température du cluster de surfaces, et
correspond à la température du cluster de surfaces, et 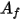 et
et 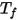 à la surface et à la température de la face de la cellule frontière dans les simulations CFA. La somme est effectuée sur toutes les faces d'un cluster de surfaces.
à la surface et à la température de la face de la cellule frontière dans les simulations CFA. La somme est effectuée sur toutes les faces d'un cluster de surfaces.