Caractéristiques du rayonnement thermique
Les caractéristiques du rayonnement thermique dépendent des propriétés suivantes de l'objet ou du corps émetteur :
• température de la surface ;
• lissage ou rugosité de la surface ;
• absorptivité spectrale ;
• puissance d'émission spectrale.
En tant qu'ondes électromagnétiques, le rayonnement thermique se compose d'une dispersion continue d'énergies de photons avec un spectre de fréquences ou de longueurs d'onde. Pour tout corps émetteur, la distribution du spectre, la valeur de crête de la longueur d'onde et la quantité totale rayonnée de toutes les longueurs d'onde varient en fonction de la température de la surface du corps émetteur. En outre, quelle que soit la température de surface, l'absorptivité, la réflectivité et l'émissivité du corps émetteur dépendent toutes de la longueur d'onde du rayonnement.
Echange d'énergie de rayonnement
Tous les corps rayonnent de l'énergie sous la forme de photons qui se déplacent dans une direction aléatoire, avec une phase et une fréquence aléatoires. Lorsque les photons rayonnés de la surface d'un corps atteignent la surface d'un autre corps, comme illustré à la figure 2.35, ils peuvent être absorbés, réfléchis et/ou transmis. Le comportement d'une surface exposée à un rayonnement incident peut être décrit par les grandeurs suivantes.
Références : R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992.
• Absorptance α : fraction du rayonnement incident absorbée à une longueur d'onde donnée.
• Réflectivité ρ : fraction du rayonnement incident réfléchie à une longueur d'onde donnée.
• Transmission τ : fraction du rayonnement incident transmise à une longueur d'onde donnée.
Les trois coefficients sont fonction de la longueur des ondes électromagnétiques du rayonnement λ. Dans les considérations énergétiques, elles doivent totaliser 1 :
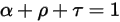
équation 2.273
Selon la loi du rayonnement thermique de Kirchhoff, l'émissivité d'un corps émetteur est égale à l'absorptivité spectrale pour toute longueur d'onde donnée en raison de la réciprocité :
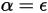
équation 2.274
où ε correspond à l'émissivité, le rapport entre l'énergie rayonnée d'un corps émetteur et celle d'un émetteur parfait (corps noir) à la même température et avec la même longueur d'onde.
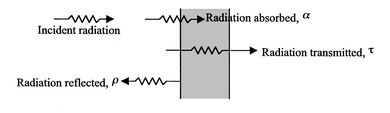
Figure 2.35
L'équation 2.273 indique que la façon dont un corps réagit vis-à-vis d'un rayonnement thermique est caractérisé par son facteur d'absorption α, sa réflexion ρ et sa transmission τ. Selon les valeurs de α, ρ et τ, les types idéalisés suivants de corps émetteur sont définis :
R. Siegel and J. R. Howell, "Thermal Radiation Heat Transfer", Hemisphere Publishing Corporation, Washington DC, 1992
• Corps opaque : ne transmet aucun rayonnement qui l'atteint, mais peut en réfléchir. τ = 0 et α + ρ = 1
• Corps transparent : transmet l'intégralité du rayonnement qui l'atteint. τ = 1 et α = ρ = 0
• Corps noir : modèle théorique proposé par Planck. Le corps noir est un objet qui absorbe tous les rayonnements électromagnétiques incidents à toutes les longueurs d'onde, quelle que soit la fréquence ou l'angle d'incidence. Si un objet émettant un rayonnement répond aux caractéristiques physiques d'un corps noir en équilibre thermodynamique, le rayonnement est appelé rayonnement du corps noir. Pour un corps noir, α = ε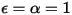 et
et 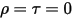
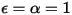 et
et 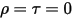
• Corps blanc : objet théorique réfléchissant complètement tous les rayons incidents de manière uniforme et dans toutes les directions. 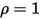 et
et 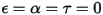
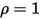 et
et 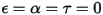
• Corps gris : corps dont 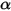 et
et 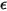 ne dépendent ni de la température, ni de la longueur d'onde.
ne dépendent ni de la température, ni de la longueur d'onde.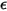 est uniforme pour toutes les longueurs d'onde. Le rayonnement d'une surface ou d'un corps gris est appelé rayonnement gris. A la différence du rayonnement gris, le rayonnement thermique avec un spectre de longueurs d'onde est appelé rayonnement non gris.
est uniforme pour toutes les longueurs d'onde. Le rayonnement d'une surface ou d'un corps gris est appelé rayonnement gris. A la différence du rayonnement gris, le rayonnement thermique avec un spectre de longueurs d'onde est appelé rayonnement non gris.
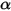 et
et 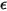 ne dépendent ni de la température, ni de la longueur d'onde.
ne dépendent ni de la température, ni de la longueur d'onde.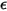 est uniforme pour toutes les longueurs d'onde. Le rayonnement d'une surface ou d'un corps gris est appelé rayonnement gris. A la différence du rayonnement gris, le rayonnement thermique avec un spectre de longueurs d'onde est appelé rayonnement non gris.
est uniforme pour toutes les longueurs d'onde. Le rayonnement d'une surface ou d'un corps gris est appelé rayonnement gris. A la différence du rayonnement gris, le rayonnement thermique avec un spectre de longueurs d'onde est appelé rayonnement non gris.Puissance de rayonnement
• Puissance 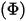 : énergie de rayonnement totale ou nette émise, réfléchie, transmise ou reçue par unité de temps pour une source donnée.
: énergie de rayonnement totale ou nette émise, réfléchie, transmise ou reçue par unité de temps pour une source donnée.
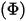 : énergie de rayonnement totale ou nette émise, réfléchie, transmise ou reçue par unité de temps pour une source donnée.
: énergie de rayonnement totale ou nette émise, réfléchie, transmise ou reçue par unité de temps pour une source donnée.• Irradiance (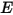 ) : puissance de rayonnement reçue par une surface
) : puissance de rayonnement reçue par une surface 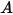 par unité de surface.
par unité de surface. 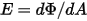
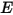 ) : puissance de rayonnement reçue par une surface
) : puissance de rayonnement reçue par une surface 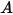 par unité de surface.
par unité de surface. 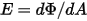
• Emittance (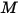 ) : puissance de rayonnement émise
) : puissance de rayonnement émise 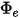 par une surface par unité de surface.
par une surface par unité de surface. 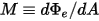
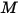 ) : puissance de rayonnement émise
) : puissance de rayonnement émise 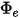 par une surface par unité de surface.
par une surface par unité de surface. 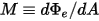
• Intensité (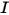 ) : puissance rayonnée dans une direction donnée (angle solide,
) : puissance rayonnée dans une direction donnée (angle solide, 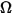 ) pour une source donnée.
) pour une source donnée. 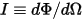
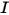 ) : puissance rayonnée dans une direction donnée (angle solide,
) : puissance rayonnée dans une direction donnée (angle solide, 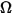 ) pour une source donnée.
) pour une source donnée. 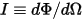
• Luminance (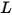 ) : puissance de rayonnement émise, réfléchie, transmise ou reçue par une surface donnée, par unité d'angle solide par unité de surface projetée.
) : puissance de rayonnement émise, réfléchie, transmise ou reçue par une surface donnée, par unité d'angle solide par unité de surface projetée. 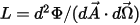
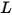 ) : puissance de rayonnement émise, réfléchie, transmise ou reçue par une surface donnée, par unité d'angle solide par unité de surface projetée.
) : puissance de rayonnement émise, réfléchie, transmise ou reçue par une surface donnée, par unité d'angle solide par unité de surface projetée. 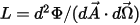
• Loi de Planck
Le rayonnement thermique émis par un corps à n'importe quelle température est composé d'une large gamme de fréquences. Dans le cas d'un corps noir, la loi de Planck décrit la distribution des fréquences de son rayonnement comme étant uniquement fonction de la température de l'objet. Planck a montré que la luminance spectrale d'un corps noir, 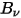 , définie comme étant la puissance émise par unité de surface du corps, par unité d'angle solide de mesure du rayonnement et par unité de fréquence,
, définie comme étant la puissance émise par unité de surface du corps, par unité d'angle solide de mesure du rayonnement et par unité de fréquence, 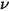 , s'exprime par la formule suivante relativement à la température du corps :
, s'exprime par la formule suivante relativement à la température du corps :
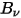 , définie comme étant la puissance émise par unité de surface du corps, par unité d'angle solide de mesure du rayonnement et par unité de fréquence,
, définie comme étant la puissance émise par unité de surface du corps, par unité d'angle solide de mesure du rayonnement et par unité de fréquence,  , s'exprime par la formule suivante relativement à la température du corps :
, s'exprime par la formule suivante relativement à la température du corps :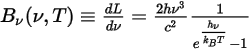
Equation 2.275
où,
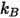 | constante de Boltzmann |
h | constante de Planck |
c | vitesse de la lumière dans le vide ou dans un milieu matériel |
La luminance spectrale est également exprimée par unité de longueur d'onde λ :
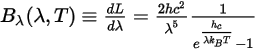
Equation 2.276
• Loi de Stefan-Boltzmann :
Avec l'intégration de la loi de Planck sur la fréquence, v, la puissance de sortie donnée par la loi de Stefan-Boltzmann est la puissance émise par un corps noir au regard de sa température. La loi de Stefan-Boltzmann est également appelée émittance du corps noir. La loi de Stefan-Boltzmann stipule que l'énergie totale rayonnée par unité de surface d'un corps noir sur toutes les longueurs d'onde par unité de temps est directement proportionnelle à la quatrième puissance de la température thermodynamique du corps noir. 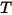 :
:
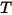 :
: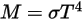
2.277
où,
σ | constante de Stefan-Boltzmann |
M | émittance |
Un corps gris, qui n'absorbe pas tous les rayonnements incidents, émet moins d'énergie totale qu'un corps noir. Avec l'introduction de émissivité,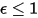 (corps noir :
(corps noir : 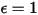 ), l'équation 2.277 est étendue à un corps gris :
), l'équation 2.277 est étendue à un corps gris :
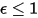 (corps noir :
(corps noir : 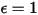 ), l'équation 2.277 est étendue à un corps gris :
), l'équation 2.277 est étendue à un corps gris :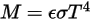
2.278
D'après la loi de Stefan-Boltzmann, la luminance et la puissance émises par un corps sont calculées comme suit :
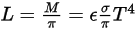
équation 2.279
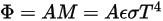
Equation 2.280
• Loi du déplacement de Wien
La loi du déplacement de Wien indique que la longueur d'onde λ, pour laquelle la luminance spectrale d'un corps noir par unité de longueur d'onde atteint sa valeur maximale, est inversement proportionnelle à la température :
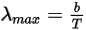
Equation 2.281
où b est la constante du déplacement de Wien.
Constantes de modèle
Les constantes utilisées dans les modèles théoriques ci-dessus sont répertoriées dans le tableau suivant :
h | constante de Planck | 6.626 069 3(11) × 10-34J-s = 4.135 667 43(35) × 10-15eV-s |
b | constante de déplacement de Wien | 2.897 768 5(51) × 10-3m-K |
kB | constante de Boltzmann | 1.380 650 5(24) × 10-23J/K = 8.617 343 (15) × 10-5eV/K |
σ | constante de Stefan-Boltzmann | 5.670 373 (21) × 10-8 W/(m2-K4) |
c | vitesse de la lumière | 299 792 458 m/s |