Modèle de particules discret
Dans le modèle de particule discret, l'écoulement de la phase dispersée est modélisé par le suivi d'un nombre spécifié de particules traversant la phase fluide continue. Dans Creo Flow Analysis, le modèle présente les hypothèses et restrictions suivantes :
• Nombre défini de particules sphériques traversant la phase d'écoulement continu du fluide. Les particules sont définies selon deux types : Avec masse (Has Mass) ou Sans masse (Massless).
• Un rayon spécifié à la position et à l'heure de la libération détermine la taille de la particule, qui reste inchangée. L'interaction entre les particules est négligeable.
• Les particules interagissent avec l'écoulement du fluide et les frontières de paroi. Le volume d'une particule ne déplace aucune quantité de fluide (fractions d'un faible volume dans la phase particulaire) et n'entraîne aucune interférence avec la géométrie (une particule surdimensionnée rentre dans un espace plus petit).
• Aucun transfert thermique ni massique n'a lieu entre la phase fluide continue et les particules. La température des particules est considérée comme étant identique à la température locale de l'écoulement du fluide.
Partant de ces hypothèses, le mouvement de chaque particule est suivi à l'aide de l'approche lagrangienne. Le suivi est effectué en formant un ensemble d'équations différentielles ordinaires dans le temps pour chaque particule, constitué d'équations de position et de vitesse. Ces équations sont ensuite intégrées pour calculer la réaction des particules au fur et à mesure qu'elles traversent le domaine de l'écoulement. Les caractéristiques de l'approche de modélisation particulaire mise en oeuvre dans Creo Flow Analysis sont les suivantes :
• Le modèle de particules discret suit l'approche d'Euler-Lagrange. La phase fluide est traitée comme un continuum en résolvant les équations de continuité et de Navier-Stokes. La phase dispersée est résolue en effectuant le suivi du mouvement de chaque particule en suivant une approche lagrangienne. La fraction de volume occupée par les particules n'est pas incluse dans le calcul de phase continue.
• Les particules de type Sans masse (Massless) se déplacent avec l'écoulement du fluide ou suivent les lignes de courant du champ de l'écoulement. La taille (ou le rayon) des particules n'a aucune incidence sur l'écoulement ou les particules. Elle est uniquement fournie à titre de référence.
• La masse des particules de type "avec masse" (Has Mass) est déterminée à l'aide des valeurs de densité et de rayon (ou de diamètre) des particules que vous spécifiez. Les forces qui agissent sur une particule et qui déterminent leur mouvement incluent la traînée particules-fluide (force d'inertie) et la gravité. Les forces de dispersion de turbulence appliquées aux particules ne sont pas prises en compte. La taille des particules affecte les forces de traînée et le post-traitement particules-fluide.
• L'échange de quantité de mouvement entre la phase fluide et les phases particulaires discrètes est modélisé de la façon suivante :
◦ Couplage unidirectionnel : seule la phase fluide affecte les mouvements des particules.
◦ Couplage bidirectionnel : les particules affectent également l'écoulement du fluide via les forces de traînée particules-fluide.
• Les interactions de type paroi-particule sont modélisées à l'aide de modèles de paroi particulaire, notamment de type "adhérence", "rebond parfait" et "rebond partiel".
• Bien que la phase fluide puisse être régulière ou irrégulière, le suivi des particules est un processus transitoire qui implique l'intégration de trajectoires de particule dans le domaine discrétisé. Selon cette approche, chaque particule est libérée ou injectée à des emplacements spécifiés à différents instants. Chaque particule est suivie de sa position de libération à sa destination, où elle quitte le domaine ou répond à certaines limites d'intégration. Enfin, on obtient une moyenne de toutes les traces de particule, et les interactions de type particules-fluide sont calculées en tant que termes sources des équations de quantité de mouvement de la phase fluide.
• La trajectoire parcourue par les particules est affichée à l'aide de la méthode de suivi des lignes d'émission associée dans le module de Particule (Particle).
Théorie du mouvement des particules
Selon l'approche lagrangienne, le mouvement des particules est déterminé par l'équilibre des forces sur la particule et les conditions dans lesquelles la particule est libérée (conditions initiales). Pour modéliser la phase particulaire discrète, les équations de mouvement des particules sont d'abord formulées en fonction de l'équilibre des forces. Vous spécifiez ensuite la frontière et les conditions initiales des particules. Enfin, l'intégration de l'équation de mouvement des particules est utilisée pour le suivi des particules.
Equations de mouvement des particules
• Equilibre des forces sur les particules
Le mouvement d'une particule discrète circulant dans un milieu fluide continu est déterminé par la force résultante qui s'y applique. Selon la deuxième loi de Newton, vous pouvez exprimer l'équilibre des forces sur les particules avec la formule lagrangienne suivante :
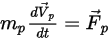
Equation 2.366
où,
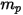 | Masse de la particule (en kg) |
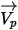 | Vitesse de la particule (en m/s) |
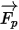 | Force nette exercée sur la particule (en N), qui affecte son accélération |
Dans un repère cartésien, si
un point 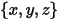 | emplacement de la particule |
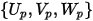 | composantes de vitesse de la particule |
Avec l'approche lagrangienne, la vitesse de la particule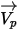 
est définie comme suit :
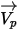est définie comme suit :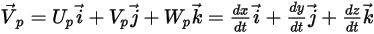
Equation 2.367
Pour une particule sphérique qui occupe un volume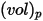 
et présente une densité 
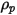ainsi qu'un diamètre 
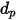(Creo Flow Analysis accepte le rayon comme entrée), la masse de la particule 
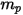est calculée comme suit :
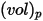et présente une densité 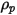ainsi qu'un diamètre 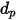(Creo Flow Analysis accepte le rayon comme entrée), la masse de la particule 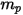est calculée comme suit :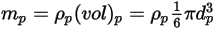
Equation 2.368
En ce qui concerne la force nette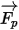 
, elle présente des facteurs tels que la force de traîné fluide-particule, la gravité et les forces dues à la rotation du domaine (forces centripète et de Coriolis). Elle est constituée des autres forces résultant de la différence de vitesse entre la particule et le fluide, ainsi que du déplacement du fluide par la particule. Dans Creo Flow Analysis, 
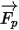peut être exprimée comme suit :
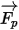, elle présente des facteurs tels que la force de traîné fluide-particule, la gravité et les forces dues à la rotation du domaine (forces centripète et de Coriolis). Elle est constituée des autres forces résultant de la différence de vitesse entre la particule et le fluide, ainsi que du déplacement du fluide par la particule. Dans Creo Flow Analysis, 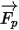peut être exprimée comme suit :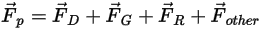
Equation 2.369
où,
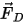 | force de traînée (en N) |
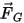 | gravité (en N) |
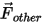 | autres forces telles que la force de masse virtuelle, la force de gradient de pression, la portance spécifiée par l'utilisateur (en N) |
Par défaut, seule la force de trainée exercée sur la particule est prise en compte.
En intégrant les équations 2.369 et 2.366, puis en divisant cela par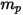 
, l'équation d'équilibre des forces résolues pour une particule présente la formule suivante :
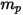, l'équation d'équilibre des forces résolues pour une particule présente la formule suivante :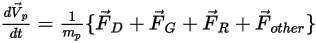
Equation 2.370
Pour fermer l'équation 2.370, vous devez calculer la contribution de chaque force. Les sous-modèles ou les formules adoptés dans Creo Flow Analysis sont décrits comme suit :
◦ Force de traînée exercée sur les particules
La force de traînée aérodynamique exercée sur une particule est proportionnelle à la vitesse de glissement de phase, la différence entre les vitesses du fluide et de la particule. En supposant que la vitesse d'écoulement du fluide est égale à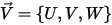 
dans le même espace où se trouve la particule à un moment donné, la force de traînée est exprimée sous la forme suivante :
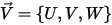dans le même espace où se trouve la particule à un moment donné, la force de traînée est exprimée sous la forme suivante :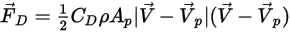
Equation 2.371
où,
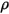 | masse volumique de la phase fluide |
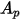 | zone de la particule projetée dans la direction de l'écoulement |
Dans le cas d'une particule sphérique de diamètre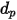 
, 
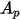est la zone maximale de coupe :
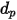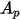, est la zone maximale de coupe :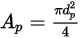
Equation 2.372
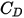est le coefficient de traînée, qui dépend du nombre de Reynolds relatif 
:
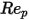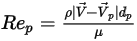
Equation 2.373
où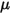 
correspond à la viscosité dynamique du fluide (Pa-s).
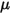correspond à la viscosité dynamique du fluide (Pa-s).Le coefficient de traînée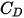 
est introduit pour tenir compte de résultats expérimentaux sur la traînée visqueuse d'une sphère solide. Différents modèles ou corrélations empiriques sont développés pour déterminer la fonction de la traînée 
(
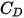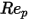) afin d'estimer l'échange fluide-particule. Pour les particules sphériques lisses, parmi de nombreux modèles, les corrections de Morsi et Alexander constituent la fonction 
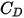la plus complète.
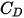est introduit pour tenir compte de résultats expérimentaux sur la traînée visqueuse d'une sphère solide. Différents modèles ou corrélations empiriques sont développés pour déterminer la fonction de la traînée 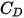(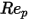) afin d'estimer l'échange fluide-particule. Pour les particules sphériques lisses, parmi de nombreux modèles, les corrections de Morsi et Alexander constituent la fonction 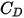la plus complète.Références : S. A. Morsi et A. J. Alexander, "An Investigation of Particle Trajectories in Two-Phase Flow Systems", J. Fluid Mech., 55(2) 193–208, 26 septembre 1972.
Elle présente l'expression générale suivante :
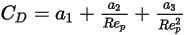
Equation 2.374
où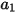 
, 
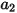et 
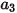sont des constantes de modèle dont les valeurs dépendent du nombre de Reynolds relatif, comme indiqué dans le tableau suivant :
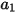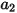, et 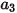sont des constantes de modèle dont les valeurs dépendent du nombre de Reynolds relatif, comme indiqué dans le tableau suivant : |  |  |  |
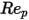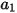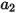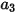0 < 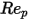 <= 0.1 | 0 | 24 | 0 |
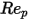0.1 <  <= 1 | 3.690 | 22.73 | 0.0903 |
1 < 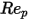 <= 10 | 1.222 | 29.1667 | -3.8889 |
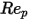10 <  <= 100 | 0.6167 | 46.50 | -116.67 |
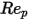100 <  <= 1000 | 0.3644 | 98.33 | -2778 |
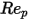1000 <  <= 5000 | 0.357 | 148.62 | -47500 |
500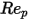0 <  <= 10000 | 0.46 | -490.546 | 57870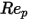0 |
 > 10000 | 0.5191 | -1662.5 | 5416700 |
Le tableau montre que, pour les nombres de Reynolds particulaires très faibles (régime visqueux),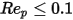 
, le coefficient de traînée affectant l'écoulement autour de particules sphériques renvoie à la Loi de Stokes :
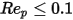, le coefficient de traînée affectant l'écoulement autour de particules sphériques renvoie à la Loi de Stokes :
Equation 2.375
Inversement, lorsque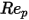 
est suffisamment grand pour que les effets inertiels dominent les effets visqueux, l'écoulement fluide-particule est en régime inertiel (ou régime de Newton). Dans le tableau, vous pouvez constater que le coefficient de traînée devient moins dépendant du nombre de Reynolds relatif. En outre, une constante de la valeur 
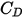est souvent utilisée à la place du modèle complet de Morsi et Alexander :
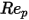est suffisamment grand pour que les effets inertiels dominent les effets visqueux, l'écoulement fluide-particule est en régime inertiel (ou régime de Newton). Dans le tableau, vous pouvez constater que le coefficient de traînée devient moins dépendant du nombre de Reynolds relatif. En outre, une constante de la valeur 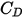est souvent utilisée à la place du modèle complet de Morsi et Alexander :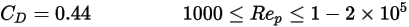
Equation 2.376
Pour les particules sphériques dans la zone de transition entre les régimes visqueux et inertiel (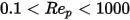
), les effets visqueux et inertiels sont tous deux importants. Par conséquent, le coefficient de traînée est une fonction complexe du nombre de Reynolds relatif, qui peut être estimée à l'aide du modèle de Morsi et Alexander ou d'autres corrélations. Par exemple, d'après le modèle de Schiller et Naumann :
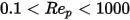), les effets visqueux et inertiels sont tous deux importants. Par conséquent, le coefficient de traînée est une fonction complexe du nombre de Reynolds relatif, qui peut être estimée à l'aide du modèle de Morsi et Alexander ou d'autres corrélations. Par exemple, d'après le modèle de Schiller et Naumann :Références : L. Schiller et Z. Naumann, "Z. Ver. Deutsch. Ing. 77. 318. 1935.
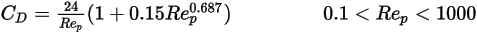
Equation 2.377
Pour simplifier l'expression du terme de la force de traînée dans l'équation 2.370, le temps de relaxation particulaire (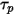
) est introduit :
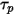) est introduit :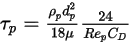
Equation 2.378
Si vous combinez les équations 2.368, 2.371, 2.372, 2.373 et 2.378, la force de traînée par unité de masse particulaire présente la formule suivante :
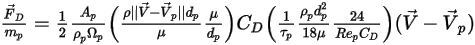
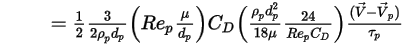
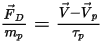
Equation 2.379
Par conséquent, l'équation par défaut de l'équilibre des forces sur les particules (seule la force de traînée est prise en compte) est exprimée sous la forme suivante :
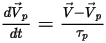
Equation 2.380
• Inclusion du terme de gravité
Par défaut, le terme de gravité n'est pas inclus dans l'équation de l'équilibre des forces sur les particules. Vous pouvez activer le terme de gravité dans Creo Flow Analysis. Pour une particule immergée dans un écoulement de fluide, l'effet de la gravité crée une force de flottaison égale au poids de la quantité de fluide déplacée par la particule. En supposant que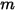 
corresponde à la masse du fluide déplacée par la particule et que 
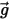soit le vecteur de gravité, la force résultante est définie comme suit :
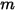corresponde à la masse du fluide déplacée par la particule et que 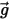soit le vecteur de gravité, la force résultante est définie comme suit :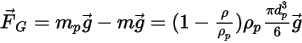
Equation 2.381
Ou la force par unité de masse particulaire est donnée comme suit :
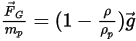
Equation 2.382
Et l'équation de l'équilibre des forces se présente comme suit :
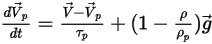
Equation 2.383
• Force de rotation exercée sur les particules
Pour les écoulements de fluide de modèle dans un référentiel en rotation, le terme de force supplémentaire résultant de la rotation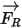 
fait partie intégrante de l'accélération des particules. Il est composé de l'effet des forces centripète et de Coriolis :
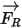fait partie intégrante de l'accélération des particules. Il est composé de l'effet des forces centripète et de Coriolis :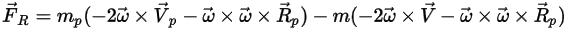
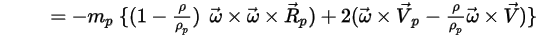
Equation 2.384
Ou la force de rotation par unité de masse particulaire est donnée comme suit :
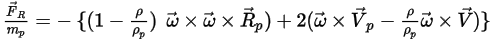
Equation 2.385
où,
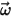 | Vitesse angulaire du référentiel en rotation |
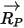 | Vecteur reliant le centre de l'axe et la position des particules |
Avec l'ajout de ce terme de force, l'équation de l'équilibre des forces sur les particules est :
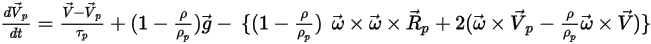
Equation 2.386
L'équation 2.386 régit le mouvement d'une particule dans un système lagrangien lorsque l'écoulement est résolu dans un référentiel en rotation.
Conditions aux limites et initiales des particules
Dans l'approche lagrangienne, le suivi des particules est une procédure transitoire. Par conséquent, vous avez besoin des conditions aux limites et initiales pour calculer les trajectoires des particules. Les conditions aux limites définissent la réaction des particules au niveau des frontières du domaine de calcul, notamment les interactions de type particules-paroi. Les conditions initiales déterminent la libération de particules à partir des frontières, y compris la position, la fréquence et la vitesse de libération, ainsi que le nombre, le type et la taille (rayon) des particules.
Conditions aux limites
Creo Flow Analysis fournit une condition aux limites de phase discrète pour déterminer la réaction des particules au niveau d'une frontière. Lorsqu'une particule atteint une frontière du domaine d'écoulement (y compris la frontière physique et l'interface solide-fluide), comme une paroi ou une frontière d'entrée, par exemple, l'un des phénomènes suivants se produit :
• La particule est reflétée par un choc élastique ou une collision inélastique.
• La particule s'échappe au travers de la frontière et est exclue du calcul au point d'impact avec la frontière.
• La particule est piégée au niveau de la paroi et est exclue du calcul au point d'impact avec la frontière.
• La particule passe dans une zone de frontière interne, telle qu'un ventilateur ou un milieu poreux.
• L'interaction entre les particules et les frontières est déterminée par des méthodes définies par l'utilisateur afin de modéliser la réaction des particules lorsqu'elles atteignent la frontière.
En fonction de la réaction des particules aux frontières, les interfaces et conditions aux limites d'écoulement sont regroupées en trois types de conditions aux limites de particules discrètes : ouverte, symétrie et paroi.
• Frontière de particules discrètes ouverte
Les particules ou les lignes de courant peuvent quitter le domaine de calcul. Une frontière ouverte est une frontière d'entrée ou de sortie de la phase d'écoulement du fluide dans le système d'Euler. Elle peut également s'appliquer à des frontières d'écoulement telles que des frontières de paroi et de symétrie. A une frontière de particule ouverte, la particule sort du domaine ou pénètre dans celui-ci selon la direction de la vitesse de la particule.
Supposons que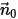 
soit le vecteur unitaire normal à la frontière ouverte, qui pointe dans la direction opposée au domaine de calcul, avec la vitesse de la particule au niveau de la frontière 
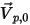. Si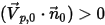 
, le vecteur de vitesse 
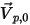pointe vers l'extérieur du domaine de calcul. Cela signifie que la particule s'échappe au travers de la frontière et est exclue du calcul au point d'impact avec la frontière.
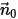soit le vecteur unitaire normal à la frontière ouverte, qui pointe dans la direction opposée au domaine de calcul, avec la vitesse de la particule au niveau de la frontière 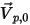. Si 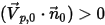, le vecteur de vitesse 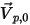pointe vers l'extérieur du domaine de calcul. Cela signifie que la particule s'échappe au travers de la frontière et est exclue du calcul au point d'impact avec la frontière.• Frontière de particule de symétrie
Lorsqu'une particule ou une ligne d'émission du domaine de calcul atteint une frontière de symétrie discrète, la condition aux limites la renvoie dans le domaine. Pour la phase de particule discrète, une frontière de particule de symétrie correspond généralement à une symétrie d'écoulement dans le système d'Euler. Il peut également s'agir d'un emplacement de libération de particules.
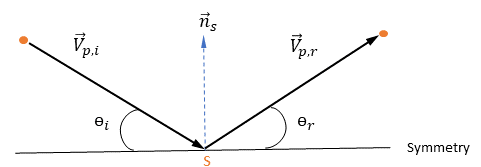
Supposons que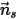 
soit le vecteur unitaire normal à l'axe de symétrie au point 
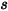de la symétrie, sa direction étant orientée vers l'extérieur de la symétrie, vers le domaine de calcul. 
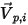et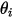 
sont introduits pour indiquer l'angle de vitesse d'impact de la particule au niveau de la frontière de particule de symétrie, comme illustré dans la figure suivante. Alors que la particule est reflétée depuis la symétrie, son énergie cinétique totale est conservée : la vitesse tangentielle reste identique, tandis que la composante de vitesse normale ne change que le signe. La condition aux limites de symétrie de particule est exprimée sous la forme suivante :
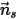soit le vecteur unitaire normal à l'axe de symétrie au point 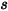de la symétrie, sa direction étant orientée vers l'extérieur de la symétrie, vers le domaine de calcul. 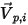et 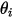sont introduits pour indiquer l'angle de vitesse d'impact de la particule au niveau de la frontière de particule de symétrie, comme illustré dans la figure suivante. Alors que la particule est reflétée depuis la symétrie, son énergie cinétique totale est conservée : la vitesse tangentielle reste identique, tandis que la composante de vitesse normale ne change que le signe. La condition aux limites de symétrie de particule est exprimée sous la forme suivante :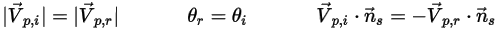
Equation 2.387
où,
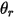 | Angle au point 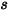 de la symétrie (en degrés) |
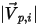 | Magnitude de la vitesse incidente de la particule (en m/s) |
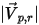 | Magnitude de la vitesse réfléchie de la particule (en m/s) |
• Frontière de particule de paroi
Pour les gouttelettes de liquide, l'interaction gouttelette-paroi dépend de la température de la paroi, de la matière de la paroi, de la rugosité, de l'angle d'impact, de la vitesse d'impact, de la présence d'un film de paroi et d'autres paramètres. Par conséquent, un ensemble de sous-modèles est utilisé pour reproduire les différents régimes d'interactions paroi-particule et tenir compte des impacts des paramètres d'écoulement et des conditions aux limites de paroi.
Dans le modèle de particules discret actuel, nous partons du principe que la forme, la taille et la masse des particules restent inchangées. En outre, nous supposons que le fluide et les particules sont en équilibre thermique. Par conséquent, une approche simple décrit le processus de collision des particules (de type "avec masse") avec les parois : pendant le processus de collision, les particules échangent de la quantité de mouvement uniquement avec la paroi, et les particules peuvent interagir avec la paroi de trois manières différentes. Ces trois manières sont le rebond parfait, l'adhérence et le rebond partiel.
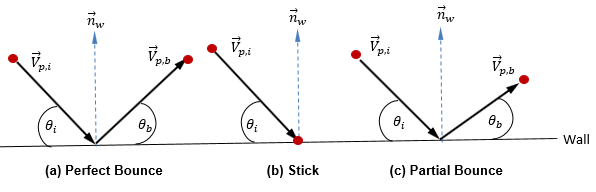
◦ Rebond parfait : une particule ou une ligne d'émission est réfléchie lorsqu'elle frappe une paroi. La quantité de mouvement et l'énergie cinétique de la particule sont parfaitement conservées. L'angle d'incidence est égal à l'angle de réflexion, tandis que la composante de vitesse normale à la paroi change de signe :
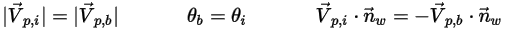
Equation 2.388
où,
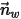 | Vecteur unitaire normal à la paroi |
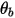 | Angle à la frontière de paroi (en degrés) |
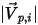 | Magnitude de la vitesse incidente de la particule (en m/s) |
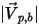 | Magnitude de la vitesse de rebond de la particule (en m/s) |
◦ Adhérence : une particule entre en collision avec la paroi, perd toute la quantité de mouvement et l'énergie dont elle dispose, et adhère à la paroi :
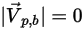
Sans tenir compte de l'accumulation de particules le long de la paroi, la particule est complètement exclue du calcul au point d'impact avec la frontière.
◦ Rebond partiel : condition de particule à la paroi entre le rebond parfait et l'adhérence. Une particule ou une ligne d'émission rebondit sur la paroi, mais perd une partie de son énergie dans une direction normale, tangentielle ou à la fois normale et tangentielle. La quantité de mouvement et l'énergie cinétique de la particule ne sont pas conservées, et l'angle d'incidence est généralement supérieur à l'angle de réflexion :
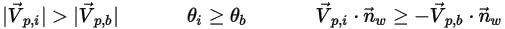
La perte d'énergie résultant de l'interaction particule-paroi est spécifiée par des entrées utilisateur :
▪ Perte d'énergie normale : spécifie la perte de la composante normale de l'énergie cinétique d'une particule au contact de la paroi.
▪ Perte d'énergie tangentielle : spécifie la perte de la composante tangentielle de l'énergie cinétique d'une particule au contact de la paroi.
Dans Creo Flow Analysis, le rebond ou l'adhérence d'une particule au contact de la paroi sont déterminés par les valeurs spécifiées des vitesses normales maximale et minimale. En supposant que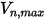 
soit la vitesse normale maximale spécifiée de la particule et que 
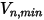corresponde à la vitesse normale minimale spécifiée de la particule, nous obtenons les conditions suivantes :
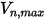soit la vitesse normale maximale spécifiée de la particule et que 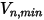corresponde à la vitesse normale minimale spécifiée de la particule, nous obtenons les conditions suivantes :▪ Si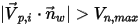 
ou 
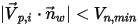, la particule rebondit au contact de la paroi.
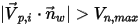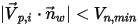ou , la particule rebondit au contact de la paroi.▪ Si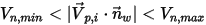 
, la particule adhère à la paroi.
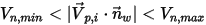, la particule adhère à la paroi.Les modèles d'interaction particule-paroi s'appliquent uniquement aux particules de type Avec masse (Has Mass). Une particule sans masse suit la ligne de courant de l'écoulement le long des parois.
Notez que les frontières de paroi de particules peuvent être des parois externes et des interfaces fluide-solide. Tout comme pour les frontières de particules ouvertes et de symétrie, les particules peuvent être libérées à partir d'une frontière de paroi.
Conditions initiales (particules au moment de leur libération)
Les conditions initiales fournissent les valeurs de départ de toutes les variables de phase discrète dépendantes qui décrivent les conditions instantanées d'une particule individuelle. Pour le suivi des particules dans un système lagrangien, la procédure de détermination des conditions initiales implique des libérations de particules (fréquences et distributions) à partir de frontières (ouverture, symétrie, paroi et interface) et l'affectation de propriétés pour chaque particule.
Lorsque vous activez l'option de libération des particules (Release Particle), les paramètres ou variables suivants sont les conditions initiales définies pour les mouvements des particules :
Intégration d'une équation de mouvement des particules
Pour suivre le mouvement des particules, les équations de trajectoire de chaque particule sont résolues (intégrées) de manière analytique ou numérique dans un système lagrangien. A partir des équations 2.367 et 2.386, les équations de mouvement sont réécrites comme suit :
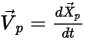
Equation 2.391
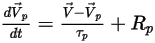
Equation 2.392
où,
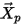 | Vecteur position de la particule |
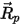 | Inclut les accélérations résultant de toutes les autres forces, (à l'exception de la force de traînée) telles que la gravité, les effets de rotation, etc. |
Les équations 2.391 et 2.392 sont un ensemble d'équations différentielles ordinaires couplées. Avec les conditions initiales et les conditions aux limites données, le déplacement particulaire (équation 2.391) est calculé à l'aide de l'intégration d'Euler explicite de la vitesse de la particule sur un pas de temps,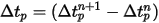 
:
:
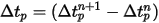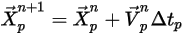
Equation 2.393
où,
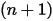 | Nouvelles valeurs |
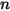 | Valeurs actuelles |
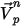 | Vitesse de la particule au pas de temps actuel |
Au premier pas de temps,
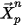 | position de libération |
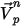| vitesse initiale |
où,
Equation 2.394
Dans cette méthode d'intégration explicite, nous supposons que la vitesse de la particule calculée au début du pas de temps reste la même pour l'intégralité du pas de temps. A la fin du pas de temps, la nouvelle vitesse de la particule est calculée en résolvant l'équation de quantité de mouvement de la particule (équation 2.392). En supposant que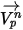 
, 
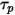et 
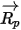soient constants sur une période 
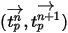, et que les propriétés du fluide soient récupérées au début du pas de temps 
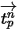, nous obtenons la solution analytique de l'équation 2.392 :
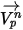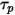, et 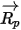soient constants sur une période 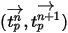, et que les propriétés du fluide soient récupérées au début du pas de temps 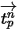, nous obtenons la solution analytique de l'équation 2.392 :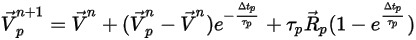
Equation 2.395
Pour évaluer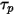 
et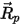 
, vous avez besoin de variables du fluide telles que la densité, la viscosité et la vitesse à la position de la particule. Elles sont considérées comme des valeurs de cellule de la phase d'écoulement du fluide dans laquelle la particule est actuellement située. Bien que ce schéma analytique soit efficace, il peut se révéler imprécis pour les pas de temps longs et dans les cas où les particules ne sont pas en équilibre hydrodynamique avec l'écoulement continu du fluide. Dans ce cas, les schémas numériques intègrent l'équation 2.392.
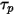et 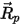, vous avez besoin de variables du fluide telles que la densité, la viscosité et la vitesse à la position de la particule. Elles sont considérées comme des valeurs de cellule de la phase d'écoulement du fluide dans laquelle la particule est actuellement située. Bien que ce schéma analytique soit efficace, il peut se révéler imprécis pour les pas de temps longs et dans les cas où les particules ne sont pas en équilibre hydrodynamique avec l'écoulement continu du fluide. Dans ce cas, les schémas numériques intègrent l'équation 2.392.Couplage particule-fluide
Dans l'approche d'Euler-Lagrange, nous supposons que l'écoulement continu du fluide affecte la réaction des particules via les forces, la chaleur et le transfert de masse. Par exemple, le terme de force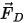 
dans l'équation d'équilibre des forces sur les particules (équation 2.370) concerne la force de traînée aérodynamique de l'écoulement sur la particule. Bien que la phase particulaire soit considérée comme étant discrète et n'entraîne aucun déplacement de volume du fluide, les particules peuvent exercer une influence de compensation sur l'écoulement du fluide par l'intermédiaire des échanges de quantité de mouvement, et éventuellement de masse et de chaleur. L'effet des particules sur l'écoulement est appelé couplage particule-fluide. Il présente deux catégories :
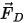dans l'équation d'équilibre des forces sur les particules (équation 2.370) concerne la force de traînée aérodynamique de l'écoulement sur la particule. Bien que la phase particulaire soit considérée comme étant discrète et n'entraîne aucun déplacement de volume du fluide, les particules peuvent exercer une influence de compensation sur l'écoulement du fluide par l'intermédiaire des échanges de quantité de mouvement, et éventuellement de masse et de chaleur. L'effet des particules sur l'écoulement est appelé couplage particule-fluide. Il présente deux catégories :• Couplage unidirectionnel
Le couplage unidirectionnel permet au fluide d'influencer les trajectoires des particules, mais les particules n'ont aucune incidence sur le fluide. Pour les particules sans masse, l'interaction particule-fluide est un couplage unidirectionnel : les particules se déplacent avec l'écoulement du fluide. Pour les particules qui présentent une masse, le couplage unidirectionnel peut être une approximation acceptable dans les écoulements avec des charges de phase dispersée faibles, où les particules ont une influence négligeable sur l'écoulement du fluide.
Pour la phase fluide continue, le champ d'écoulement est calculé comme un écoulement de fluide monophasique, sans la présence d'une phase particulaire dispersée. Le suivi du mouvement des particules est ensuite effectué en fonction du champ d'écoulement calculé et des conditions initiales. Dans le cas d'un écoulement en régime permanent, le suivi des particules est effectué une fois que la solution d'écoulement convergée de la phase continue est obtenue en résolvant les équations de continuité et de Navier-Stokes. Dans le cas de la simulation d'un écoulement en régime transitoire, le suivi du mouvement des particules est effectué à la fin de chaque pas de temps de la simulation d'écoulement.
• Couplage bidirectionnel
Dans le cas des particules "avec masse", le couplage bidirectionnel permet au fluide d'influencer les trajectoires des particules. Il tient également compte des effets des particules sur la phase fluide continue. Sans tenir compte des transferts massique et thermique, l'interaction bidirectionnelle entre le fluide et les particules ne concerne que l'échange de quantité de mouvement. La quantité de mouvement transférée de la phase continue vers la phase discrète est calculée en effectuant le suivi de la quantité de mouvement acquise ou perdue par chaque particule lorsqu'elle traverse un volume de contrôle. Dans un couplage bidirectionnel, les échanges de quantité de mouvement particule-fluide doivent être inclus dans les équations de quantité de mouvement pour tenir compte de l'effet des trajectoires des phases discrètes sur le continuum. Dans l'équation 2.386, seule la force de traînée tient compte de l'échange de quantité de mouvement particule-fluide et est ajoutée aux équations de quantité de mouvement. Notez que, pour les particules sans masse, aucun terme d'échange n'est calculé entre elles et l'écoulement du fluide, de sorte que les trajectoires des phases discrètes n'ont aucune incidence sur le continuum.
Pour inclure les effets de traînée particule-fluide dans les équations de quantité de mouvement de phase continue, la force de traînée de chaque particule se déplaçant dans l'écoulement est appliquée dans le volume de contrôle où la particule est située au cours du pas de temps. Pour la particule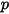 
, nous calculons sa source d'inertie résultant de la traînée 
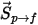à l'aide de l'équation différentielle suivante :
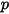, nous calculons sa source d'inertie résultant de la traînée 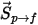à l'aide de l'équation différentielle suivante :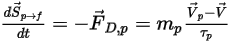
Equation 2.396
Et la source de particule transférée vers la phase continue correspond au terme source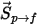 
que vous multipliez par le débit particulaire (débit massique divisé par la masse de la particule) :
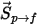que vous multipliez par le débit particulaire (débit massique divisé par la masse de la particule) :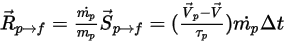
Equation 2.397
où,
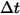 | Pas de temps |
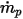 | Débit massique particulaire |
En supposant que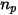 
corresponde au nombre de particules traversant un volume de contrôle au pas de temps 
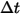, nous obtenons le terme source total particule-fluide suivant :
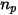corresponde au nombre de particules traversant un volume de contrôle au pas de temps 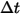, nous obtenons le terme source total particule-fluide suivant :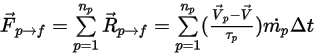
Equation 2.398
Avec l'ajout de la force de traînée fluide-particule, les équations gouvernantes résolues pour la phase continue sont désormais exprimées comme suit :
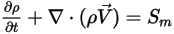
Equation 2.399
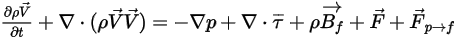
Equation 2.400
Avec un couplage unidirectionnel,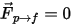 
la phase fluide continue est régie par les équations de continuité et de quantité de mouvement monophasiques exactes. Dans le cas d'un couplage bidirectionnel, nous ajoutons le terme source de force de traînée particule-fluide. L'équation 2.399 et l'équation 2.400 sont résolues de la même manière que pour un écoulement monophasique.
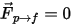la phase fluide continue est régie par les équations de continuité et de quantité de mouvement monophasiques exactes. Dans le cas d'un couplage bidirectionnel, nous ajoutons le terme source de force de traînée particule-fluide. L'équation 2.399 et l'équation 2.400 sont résolues de la même manière que pour un écoulement monophasique.