Modèles de cavitation
Creo Flow Analysis et le modèle de Singhal et autres d'origine partent toujours du principe que le fluide en cours d'utilisation dans les écoulements cavitants est un mélange de liquide, de vapeur et de certains gaz non condensables. Par défaut, les modèles de cavitation tiennent compte des changements de phase des liquides comme des vapeurs, ainsi que de l'effet des gaz non condensables. En fonction de l'approche de modélisation de l'effet des gaz non condensables, cinq modèles différents sont fournis dans la table suivante pour la prédiction de l'aération et de la cavitation dans un système liquide. Ces modèles sont décrits en détail dans la présente section.
|
Modèles pour les gaz non condensables
|
Description
|
|---|---|
|
Fraction massique de gaz constante
|
La fraction massique des gaz non condensables est constante et considérée comme hors de la solution avec des bulles compressibles minuscules
|
|
Fraction massique de gaz variable
|
Elle est similaire au modèle de fraction massique de gaz constante, à l'exception du fait que la fraction massique des gaz non condensables peut varier, tout comme les admissions qui peuvent introduire des fractions massiques différentes
|
|
Modèle de gaz dissous à l'équilibre
|
La fraction massique des gaz non condensables dissous dans le liquide est égale à la valeur d'équilibre
|
|
Modèle de gaz dissous
|
La fraction massique des gaz non condensables dissous dans le liquide dépend du taux d'absorption et de désorption et de la valeur d'équilibre
|
|
Modèle de gaz complet
|
Combine le modèle de gaz dissous et la fraction massique de gaz variable
|
Modèle de fraction massique de gaz constante
Il correspond au modèle de cavitation par défaut ou de base dans Creo Flow Analysis. Il est basé sur le travail de Singhal et autres. Ce modèle suppose que le gaz non condensable toujours présent dans le fluide en cours d'utilisation est un gaz qui ne peut pas se dissoudre ou qu'il est constitué de bulles de gaz libres respectant la loi des gaz parfaits. Bien que l'ensemble des gaz non condensables décrits au préalable puisse se dilater sans contrainte en cas de baisse de pression dans les zones de cavitation, la fraction massique des gaz non condensables est décrite préalablement et reste identique dans l'écoulement cavitant :
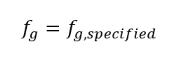
équation 2.217
où la valeur fg,spécifiée est une valeur spécifiée par l'utilisateur.
La densité des gaz non condensables suit la loi des gaz parfaits :
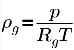
équation 2.218
où T est la température du fluide, qui est décrite au préalable (écoulement isotherme) ou que vous pouvez obtenir en résolvant l'équation 2.168 relative à la conservation d'énergie du mélange lorsque le transfert de chaleur est pris en compte. D'après l'équation 2.173, la fraction volumique des gaz non condensables est la suivante :
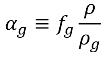
équation 2.219
Bien que la fraction massique des gaz non condensables soit fixe et présente généralement une valeur faible de 1.5e-05 ou 15 ppm dans l'eau naturelle, sa fraction volumique αg varie et peut être plus élevée. Dans les empreintes ou zones de faible pression, le gaz non condensable s'efforce de repousser la vapeur afin d'occuper l'espace vide. Le résultat dépend de la densité de la vapeur et du gaz.
Pour le transfert de masse de liquide/vapeur, l'équation 2.194 et l'équation 2.195 servent de base pour construire les termes source et puits de la cavitation dans l'équation 2.169 de la fraction massique de la vapeur. Plus spécifiquement, le rayon de la bulle, RB doit être estimé à l'aide des quantités d'écoulement connues pendant la croissance et l'effondrement des bulles. Selon Singhal et autres, si la taille classique des bulles RB est identique à leur taille limite (taille maximale possible), la valeur RB est déterminée par l'équilibre entre les forces de traînée aérodynamique et de tension de surface. La corrélation utilisée dans le secteur nucléaire est la suivante :
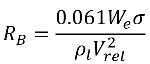
équation 2.220
où Vrel est la grandeur de la vitesse relative du liquide/de la vapeur. Dans le régime d'écoulement des bulles, dans le cadre duquel se produit la cavitation, la valeur Vrel est généralement peu élevée (environ 5 à 10 % de la vitesse du liquide). En utilisant différents arguments limites, par exemple RB →0 comme αv →0 et le fait que les taux de changement de phase par volume unitaire doivent être proportionnels aux fractions volumiques (ou fractions massiques) de la phase d'atome donneur, on obtient les expressions suivantes pour les taux de condensation/génération de vapeur afin de compléter le modèle de cavitation, comme suit :
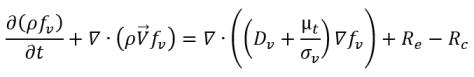
équation 2.221
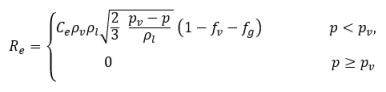
équation 2.222
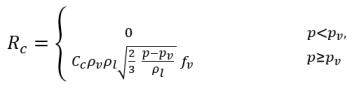
équation 2.223
où les valeurs Ce et Cc correspondent aux coefficients d'évaporation et de condensation. Il peut s'agir de valeurs constantes spécifiées par l'utilisateur, définies par défaut sur la valeur 1.0, ou de fonctions correspondant à des quantités d'écoulement connues. Dans l'équation 2.222 et l'équation 2.223, un nouveau seuil de pression ρv est intégré pour remplacer la pression de vapeur de saturation ρsat dans l'équation 2.194 et l'équation 2.195. D'après Singhal et autres, pour prendre en compte l'effet de la turbulence sur les écoulements cavitants observé lors d'investigations expérimentales, une valeur locale des fluctuations de pression turbulente fournie par Hinze :
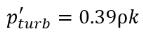
équation 2.224
est ajouté à la pression de vapeur de saturation afin d'élever la valeur de pression du seuil de changement de phase au niveau :
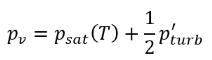
équation 2.225
Pour les écoulements laminaires, pv=psat(T)
Lorsque le transfert de chaleur est pris en compte et que toutes les densités de phase (notamment les gaz non condensables, vapeurs et liquides) sont soumis aux changements liés à la température, la pression de la vapeur de saturation psat est également une fonction de la température. En conséquence, l'effet thermique direct sur la cavitation peut être pris en compte dans ce modèle de cavitation.
Modèle de fraction massique de gaz variable
Ce modèle part du principe que les gaz non condensables sont toujours des gaz libres, qui ne peuvent pas se dissoudre dans le liquide. Cependant, la fraction massique n'est plus une constante décrite au préalable, comme dans le modèle de fraction massique de gaz constante. A l'inverse, la distribution de la fraction massique locale est régie par une équation de transport. Lorsque le transfert de masse de liquide/vapeur est modélisé par le même modèle de cavitation référencé dans l'équation 2.221, l'équation 2.222 et l'équation 2.223. A des fins de clarification, l'ensemble complet d'équations de modélisation est indiqué ci-dessous :
• Changement de phase liquide/vapeur
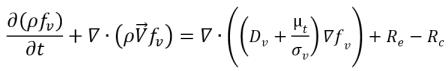
équation 2.226
où
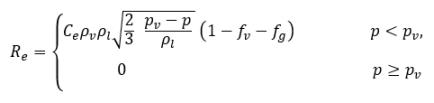
équation 2.227
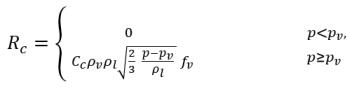
équation 2.228
• Equation de transport des gaz non condensables
D'après l'équation 2.199, l'équation de transport des gaz non condensables (fg) est la suivante :
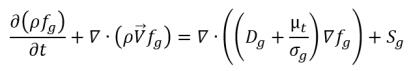
équation 2.229
où la valeur Sg correspond à la source externe ou définie par l'utilisateur des gaz non condensables.
Modèle de gaz dissous à l'équilibre
Dans les écoulements cavitants, les gaz non condensables présents dans le fluide sont dissous dans un liquide, ou libérés dans ce dernier, afin de créer un équilibre dynamique des concentrations massiques entre les phases liquides et gazeuses. Le modèle de gaz dissous à l'équilibre part du principe que la fraction massique de la quantité totale de gaz non condensable reste constante. Toutefois, une partie est dissoute dans le liquide afin de satisfaire immédiatement à la condition d'équilibre locale. En termes mathématiques, outre les mêmes modèles de transfert de masse de vapeur et d'équation de fraction massique de la vapeur, ce modèle résout une équation de transport supplémentaire pour la fraction massique des gaz dissous fgd, qui est censée être à l'état d'équilibre en permanence. Les équations de modélisation sont les suivantes :
• Changement de phase liquide/vapeur
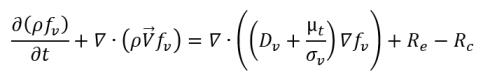
équation 2.230
où
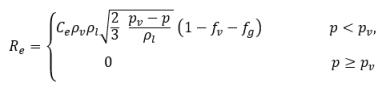
équation 2.231
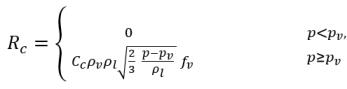
équation 2.232
• Absorption/dissolution ou libération des gaz
D'après l'équation 2.197, l'équation 2.211 et l'équation 2.212, l'équation de transport des gaz dissous a la forme suivante :
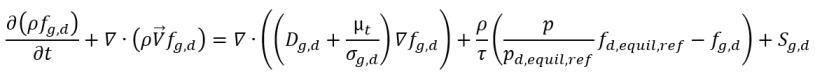
équation 2.233
où
Sg,d | loi relative à la dissolution ou la libération des gaz, définie par l'utilisateur |
fd,équil,réf | fraction massique d'équilibre des gaz dissous au niveau de la pression de référence pd,équil,réf |
fd,équil,réf et pd,équil,réf | valeurs spécifiées par l'utilisateur |
Dans ce modèle d'équilibre, l'échelle temporelle Γ approche de zéro, de sorte que le transfert de masse s'effectue presque instantanément. Notez que dans l'équation 2.231, le gaz libre présente la fraction massique fg,f, au lieu de fg. La fraction massique des gaz libres s'obtient à partir de la condition :
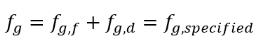
équation 2.234
où la valeur fg,spécifiée est une valeur spécifiée par l'utilisateur.
Modèle de gaz dissous
Ce modèle assouplit la condition selon laquelle le gaz dissous dans le liquide est toujours à l'état d'équilibre. Au lieu d'être déterminée par la condition d'équilibre avec transfert de masse instantané, la fraction massique des gaz dissous (fg,d) dépend du transport du composant et du taux de dissolution ou de libération (taux fini). Par conséquent, le modèle de gaz dissous partage les mêmes formulations de modélisation que le modèle de gaz dissous à l'équilibre : équation 2.230-équation 2.234. Toutefois, les taux finis de transfert de masse pour la dissolution et la libération des gaz sont caractérisés par des échelles temporelles différentes (Γ). Pour l'absorption ou la dissolution des gaz dans le liquide, la valeur Γ est fournie par un temps d'absorption spécifié (par défaut, la durée de dissolution des gaz dissous est de 10 secondes). Pour la libération des gaz dissous du liquide, le taux de transfert de masse est régi par un temps de libération des gaz spécifié (par défaut, le temps de libération des gaz dissous Γ est de 10 secondes).
Modèle de gaz complet
Le modèle de gaz complet est une combinaison du modèle de gaz dissous et du modèle de gaz variable. La fraction massique des gaz non condensables varie en fonction du temps et de l'espace, alors que la dissolution, ou l'absorption et la libération des gaz peuvent également survenir dans le cas de gaz non condensables. L'ensemble complet d'équations de modélisation est indiqué ci-dessous :
• Changement de phase liquide/vapeur
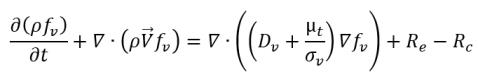
équation 2.235
où
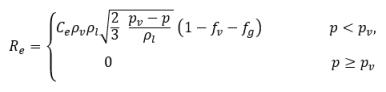
équation 2.236
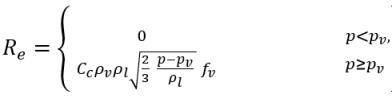
équation 2.237
• Transport des gaz non condensables
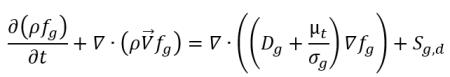
équation 2.238
• Dissolution ou libération des gaz
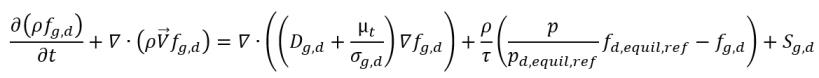
équation 2.239