空蝕模型理論
在蒸汽傳輸方程式 2.169 中,Re 與 Rc 是與空蝕流中蒸汽氣泡的增長與塌陷相關的質量傳遞源項。這些項用於解釋空蝕過程中汽相與液相之間的質量交換。Re 與 Rc 會基於用來描述單一蒸汽氣泡在液體中的增長的 Rayleigh-Plesset 方程式進行建模。
液汽質量傳遞
欲推導空蝕中淨相變率的運算式,請考慮使用滑動速度為零的不可壓縮液汽二相流 (不考慮不凝結氣體)。如果引入 R 表示從液體到蒸汽的淨質量傳遞率,則液體與蒸汽體積分數方程式與總質量連續性方程式如下所示:
• 液相:
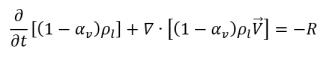
方程式 2.179
• 汽相:
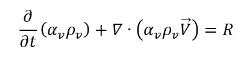
方程式 2.180
• 混合物 (總質量連續性)
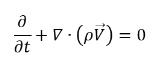
方程式 2.181
在液汽二相系統中,可透過蒸汽體積分數與相密度表示混合物密度 ρ:
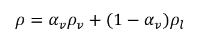
方程式 2.182
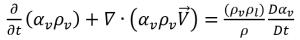
方程式 2.183
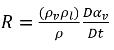
方程式 2.184
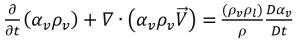
方程式 2.185

方程式 2.186
根據方程式 2.185 與方程式 2.186,可瞭解到,當液相與汽相之間的滑動速度為零時,可透過額外的蒸汽質量分數傳輸方程式將空蝕建模為單相流;或透過液汽質量傳遞建模為尤拉 多相混合流。如果不考慮擴散與相速度差的影響,這兩個方法在數學運算方面相同。Creo Flow Analysis 使用單相方法對空蝕流進行建模。
氣泡動力學考量
在大多數自然現象及工程系統中,液體中存在足夠數量的核 (例如氣泡、不凝結氣體等),從而為空蝕初生提供了條件。因此,欲對空蝕過程進行建模,應主要關注正確解釋氣泡增長與塌陷過程。假設流動液體中液體與蒸汽氣泡之間的滑動速度為零,可透過描述液體中氣體氣泡增長的廣義 Rayleigh Plesset 方程式來推導氣泡動力學方程式:
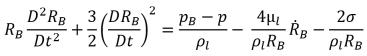
方程式 2.187
其中,
RB | 氣泡半徑 |
pB | 氣泡內部壓力 (不存在其他氣體時,假設為液體溫度下的蒸汽壓力) |
p | 液體中氣泡周圍的壓力 |
σ | 液體與蒸汽之間的表面張力係數 |
此方程式透過機械平衡 (沒有阻礙氣泡增長的熱障礙) 推導得出。
如果忽略二階時間導數 (適用於低振盪頻率)、黏性阻尼項與表面張力,則會取得適用於漸進狀態之方程式 2.187 的簡化運算式:
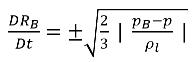
方程式 2.188
此簡化 Rayleigh Plesset 方程式提供用於在空蝕模型中引入氣泡動力學效果的物理方法。氣泡半徑可增加或減小,具體取決於 (pB–p) 的符號︰當 p<(pB 時,氣泡會增長;當 p>pB 時,氣泡會塌陷。因此,方程式 2.188 可改寫為如下所示:
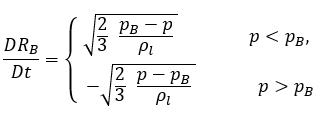
方程式 2.189
如果 η 為液體中的蒸汽氣泡數密度 (單位體積內存在的氣泡數),並且所有蒸汽氣泡都是具有相同半徑 RB 的完美球體,則汽相體積分數如下:
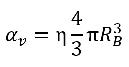
方程式 2.190
假設蒸汽氣泡無法在液體中形成或破裂,但氣泡可以在空蝕過程中增長 (蒸發) 和塌陷 (凝結)。在方程式 2.190 中,蒸汽氣泡數密度 (η) 保持恆定,但氣泡半徑 (RB) 將增大或減小。蒸汽體積分數的時間導數計算如下
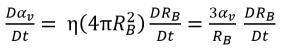
方程式 2.191
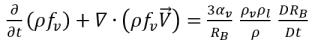
方程式 2.192
透過套用方程式 2.189,單位體積內液體與蒸汽之間的淨質量傳遞率形式如下:
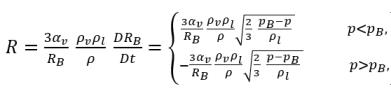
方程式 2.193
其中方程式 2.193表示在空蝕中,單位體積質量傳遞率 (R) 是汽相與液相密度的函數 (成正比),並且還與混合物密度成反比。由於方程式 2.192 是直接從相與混合流質量連續性推導得到的,因此它是精確的並且應能夠準確地表示空蝕中液相與汽相之間的質量傳遞。引入氣泡動力學之後,方程式 2.193 會使用類似方法對兩個相反 (即在物理上不同) 的質量傳遞過程進行建模:從液體到蒸汽 (氣泡增長或蒸發),以及從蒸汽到液體 (氣泡塌陷或凝結)。對於蒸汽質量分數傳輸方程式 2.192,氣泡增長為源項,而氣泡塌陷則視為匯項。
在實際空蝕模型中,局部遠場壓力 p 通常視為與单元中心壓力相同。如果不存在溶解氣體、質量傳遞與黏性阻尼,則氣泡壓力 pB 等於飽和蒸汽壓力 (psat,材料屬性),即 pB=psat
• 如果局部流動壓力低於飽和蒸汽壓力,即 p<psat,則僅會發生蒸發,因此:
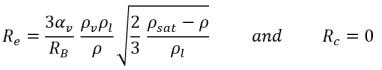
方程式 2.194
• 如果局部流動壓力大於飽和蒸汽壓力,即 p>psat,則僅存在凝結:
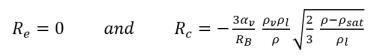
方程式 2.195
氣體吸收/溶解與釋放
工作流體中通常存在不凝結氣體,這些氣體會對空蝕造成重大影響。有時,不凝結氣體會隨著流體流動自由傳輸,也會在液體中溶解或釋放,本質上是為了在液相和氣相之間實現質量濃度動態平衡。液體中的氣體吸收或溶解與釋放也是一種液氣質量傳遞現象,這種現象由質量濃度差和梯度驅動。為了對空蝕流進行建模,還需要考慮混合流中不凝結氣體及可能的液氣質量傳遞的影響。
假設在液氣二相流中,液相 (溶解氣體) 與氣相 (自由氣體) 中均存在不凝結氣體 (例如空氣或氧氣),每個相中的氣體質量分數傳輸方程式如下:
• 自由氣體 (氣相)
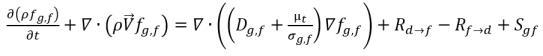
方程式 2.196
• 溶解氣體 (液相)
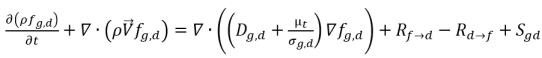
方程式 2.197
其中,
fg,f | 自由氣體的質量分數 |
fg,d | 自由氣體與溶解氣體的質量分數 |
Sg,f, Sg,d | 外部源或使用者定義的源。 |
Dg,f | 自由氣體與溶解氣體的擴散係數 |
Dg,d | 溶解氣體的擴散係數 |
如果不凝結氣體的質量分數預先規定為 fg,則可得:
fg=fg,f
或者,可透過求解下列方程式取得其在空間和時間上的傳輸:
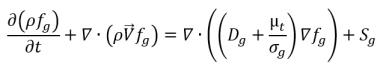
方程式 2.199
當兩個相接觸時,易發生自由氣體 f 與溶解氣體 d 從一個相傳輸至另一相,以實現二相之間的動態平衡。平衡模型假設體積質量傳遞率取決於質量濃度差或梯度:
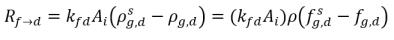
方程式 2.200
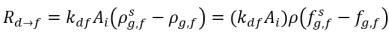
方程式 2.201
其中,
AI | 液氣界面面積 |
kf,d(=kd,f) | 整體體積質量傳遞係數 |
ρg,d(=ρfg,d) | 溶解氣體的局部質量濃度 |
ρg,f(=ρfg,f) | 自由氣體的局部質量濃度 |
 | 溶解氣體在其主相中的平衡質量濃度 |
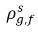 | 自由氣體在其主相中的平衡質量濃度 |
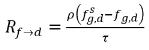
方程式 2.202
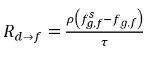
方程式 2.203
通常,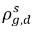 與
與 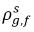 不同 (不連續性)。兩個濃度之間存在明確的平衡曲線,它取決於溫度、壓力以及混合物成份。該曲線通常為單調、非線性曲線,通常表示為與係數
不同 (不連續性)。兩個濃度之間存在明確的平衡曲線,它取決於溫度、壓力以及混合物成份。該曲線通常為單調、非線性曲線,通常表示為與係數 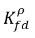 的擬線性關係
的擬線性關係
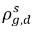 與
與 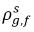 不同 (不連續性)。兩個濃度之間存在明確的平衡曲線,它取決於溫度、壓力以及混合物成份。該曲線通常為單調、非線性曲線,通常表示為與係數
不同 (不連續性)。兩個濃度之間存在明確的平衡曲線,它取決於溫度、壓力以及混合物成份。該曲線通常為單調、非線性曲線,通常表示為與係數 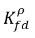 的擬線性關係
的擬線性關係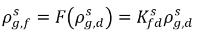
方程式 2.204
其中 Kf,d 通常使用物理定律或經驗關係式來確定。一個常用的方法就是是遵循亨利定律,該定律提供了廣義平衡關係。這表示對於與氣相接觸的液體混合物,自由氣體的局部壓力 ρg,f 等於液相中溶解氣體的平衡莫爾分數 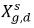 與亨利常數 Hx 之積︰
與亨利常數 Hx 之積︰
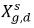 與亨利常數 Hx 之積︰
與亨利常數 Hx 之積︰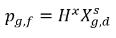
方程式 2.205
如果自由氣相遵循理想氣體定律,則根據道爾頓分壓定律可給出下列方程式:
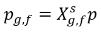
方程式 2.206
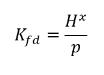
方程式 2.207
因此,亨利常數具有壓力單位,並且可視為參照壓力。假設對於與氣體接觸的理想液體混合物,亨利常數為飽和蒸汽壓力 psat,則方程式 2.207 也可如下所示︰
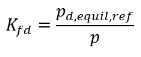
方程式 2.208
其中 pd,equil,ref 是溶解平衡質量分數的參照壓力。方程式 2.204 改寫如下:
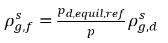
方程式 2.209
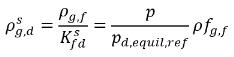
方程式 2.210
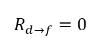
方程式 2.211
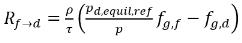
方程式 2.212
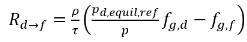
方程式 2.213
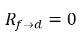
方程式 2.214
請注意,當部份不凝結氣體溶解到液體中時,僅氣相中存在可自由膨脹氣體 fg,f。因此,混合物密度計算如下:
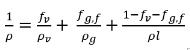
方程式 2.215
自由氣體的體積分數如下:
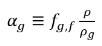
方程式 2.216
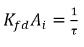 具有反演時間單位 1/s,表示質量傳遞效率。因此,
具有反演時間單位 1/s,表示質量傳遞效率。因此,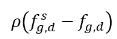 與
與 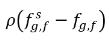 為質量濃度差/梯度,即不凝結氣體的吸收/溶解與釋放的驅動力。它表示,跨二相的不凝結氣體傳輸需滿足質量濃度偏離其平衡狀態這一條件。質量傳遞方向會根據兩個相的局部與平衡質量濃度使系統趨於平衡。根據平衡模型,可得下列內容:
為質量濃度差/梯度,即不凝結氣體的吸收/溶解與釋放的驅動力。它表示,跨二相的不凝結氣體傳輸需滿足質量濃度偏離其平衡狀態這一條件。質量傳遞方向會根據兩個相的局部與平衡質量濃度使系統趨於平衡。根據平衡模型,可得下列內容: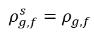 。根據
。根據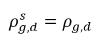 。根據
。根據