統御方程式
在空蝕傳輸模型中,液體與氣體 (蒸汽與其他可能的氣體) 混合物的總體運動被視為可變密度單相流。混合流與多成分流的一般統御方程式組相同,而專門建立了混合流的傳輸方程式以控制在空蝕中產生的蒸汽質量分數。欲對不凝結氣體產生的影響進行建模,也可能需要求解氣體質量分數的其他傳輸方程式,具體取決於氣體模型。針對空蝕流求解的完整一般統御方程式組如下:
• 連續性
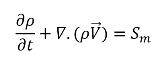
方程式 2.166
其中 Sm 為獨立於空蝕的淨外部源或使用者源
• 動量方程式
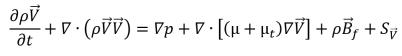
方程式 2.167
• 能量方程式
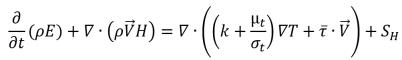
方程式 2.168
• 蒸汽質量分數方程式
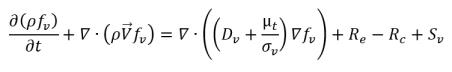
方程式 2.169
其中,
fv | 蒸汽質量分數 |
Re | 蒸汽產生源 (蒸發) |
Rc | 匯項 (凝結) |
Sv | 外部或使用者定義的蒸汽源項 |
• 不凝結氣體 (NCG) 質量分數方程式

方程式 2.170
這是不凝結氣體 (NCG) 的一般傳輸方程式,包括產生項、匯項與外部或使用者定義的源項。
根據不同的空蝕模型,可針對不凝結氣體、溶解氣體等求解不同的方程式 (介於零與兩個之間)。
在傳輸方程式中,混合物屬性使用下列關係計算:
• 混合物密度
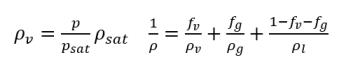
方程式 2.171
其中,
ρv | 蒸汽密度 |
ρg | 不凝結自由氣體密度 |
ρl | 液體密度 |
液體與蒸汽密度為恆定 (不可壓縮) 與/或可變 (可壓縮)。但是,在空蝕模型中,不凝結自由氣體密度始終被視為理想氣體密度。請注意,在方程式 2.171 中,液體質量分數 ƒl 使用物理限制計算:所有成分的質量分數總和為 1,即:
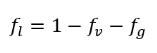
方程式 2.172
在空蝕流中,相關參數為蒸汽 αv 或氣相總體積分數 αtotal,可根據已求解的質量分數 ƒv 與自由氣體質量分數 ƒg 進行推斷︰

方程式 2.173
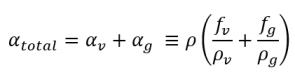
方程式 2.174
• 混合物黏度
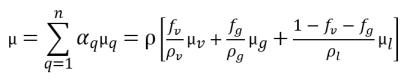
方程式 2.175
其中,
μv | 蒸汽動態黏度 |
μg | 不凝結自由氣體 |
μl | 液體 |
• 混合物熱屬性
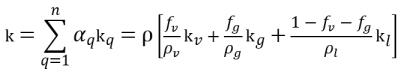
方程式 2.176
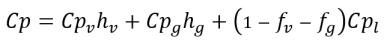
方程式 2.177
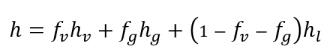
方程式 2.178
其中,
k | 熱導率 |
Cp | 定壓過程的比熱 |
h | 比焓 |
針對所涉及的成分將以蒸汽 (v)、不凝結自由氣體 (g) 和液體 (l) 的特定下標表示。