수치 고려 사항
균질 다상 모델에서 속도 슬립을 고려하지 않으면 혼합물 운동량 방정식 및 평면 부피 흐름 수식의 해를 구할 때 특별한 처리가 필요하지 않습니다. 이는 이러한 방정식이 가변 밀도 단일 위상 흐름을 지배하는 해당 방정식과 동일하기 때문입니다. 이 항목은 압력 보정 방정식의 구성, 위상 부피 분율 방정식의 처리, 특히 VOF 모델의 계면 분해 기법에 가장 중점을 둡니다.
부피 연속성 방정식
연속성 제약 조건을 충족하고 수치 안정성을 보장하기 위해 질량 연속성 대신 총 부피 연속성을 기반으로 압력 보정 방정식이 작성됩니다. qth 위상 연속성/부피 분율 방정식 2.57을 위상 기준 밀도 ρrq로 나누고, 모든 위상을 함께 결합할 때 질량 보존의 법칙을 충족하는 총 부피 연속성 방정식을 구합니다.
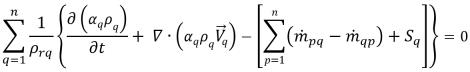
방정식 2.135
여기서 위상 기준 밀도가 일반적으로 위상 밀도 ρrq = ρq로 설정됩니다.
Ω를 계산 셀의 부피로 도입하고 검사 부피에 대한 방정식 2.135를 적분하여 이산화 대수 방정식을 생성합니다.
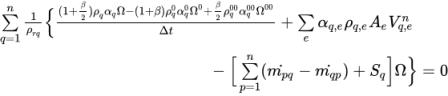
방정식 2.136
"수"에 설명된 단일 위상 압력 기반 풀이 시스템과 동일한 접근 방식을 사용하고 다음을 가정하는 경우
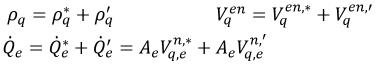
방정식 2.137
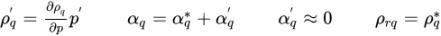
방정식 2.138
방정식 2.136을 다음 보정 방정식으로 재조정할 수 있습니다.
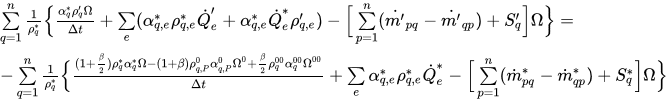
방정식 2.139
여기서 * 및 '는 이전 값 및 보정을 나타냅니다.
Δt | 시간 단계 |
Ae | 면 e의 면적 |
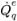 | 부피 흐름 |
단일 위상 압력 기반 풀이 시스템과 동일한 접근 방식에 따라 속도 및 압력 보정을 연결하고 다상 흐름에 대한 압력 보정 방정식을 구하기 위한 SIMPLE 유형의 알고리즘(Simple, SimpleC 및 SimpleS)을 적용합니다.
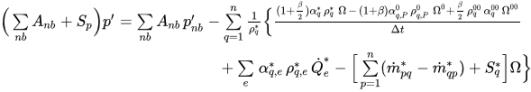
방정식 2.140
여기서 각 항목은 다음을 나타냅니다.
Anb | 연결 계수 |
Sp | 선형화 항 |
위상 부피 분율 방정식
위상 부피 분율의 운송은 위상 질량 보존에 의해 지배됩니다. 압력 보정 방정식을 형성하는 데 총 부피 보존이 적용되므로 위상 부피 분율의 해를 구한 실제 방정식도 수치 일관성을 위해 부피 보존 형식으로 존재합니다.
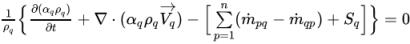
방정식 2.141
일반적으로 n상 시스템의 경우 (n–1) 방정식만 해를 구하고, 물리적 제약 조건에서 nth 위상을 구합니다.
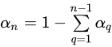
방정식 2.142
이산화 접근 방식에 따라 방정식 2.141의 적분 형식은 다음과 같습니다.
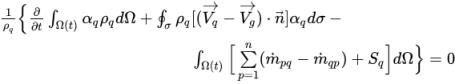
방정식 2.143
운동량, 에너지 및 총 부피 보존 방정식에서 제공된 대로 공간 및 시간 이산화 기법은 수치 정확성을 위해 반드시 필요합니다. 부피 분율 방정식의 경우 표준 암시적 시간 기법 이외에도 VOF 모델에서 계면을 보다 정확하게 캡처할 수 있도록 고분해능 이송 기법과의 명시적 시간 마칭을 사용하는 것이 일반적입니다. 암시적 VOF 수식과 명시적 VOF 수식 모두 이 단원에서 자세히 설명합니다.
• VOF 암시적 수식
VOF 암시적 수식을 사용하는 경우 이산화된 위상 부피 분율 방정식의 일반 표현식은 다음과 같습니다.
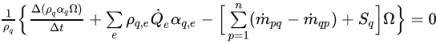
방정식 2.144
이 방정식에서는 현재 시간 단계의 위상 부피 분율 αq가 현재 시간 단계에서 다른 수량의 함수입니다. 따라서 운동량, 에너지 및 압력 보정 방정식으로 이산화된 부피 분율 방정식 2.144를 각 시간 단계에서 반복해서 해를 구합니다. Creo Flow Analysis에서 채택된 암시적 수식은 다음과 같이 요약됩니다.
◦ 이송 기법(Advection Schemes) - 체적 유속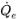 
은 현재 시간 단계에서 흐름 필드를 기반으로 계산됩니다. 면 값 αq,e는 셀 중심 값 αq,P,αq,E 및 인접 셀 P 및 E의 구배(
, 
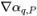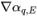)를 기반으로 근사치를 구합니다. 패시브 스칼라 방정식처럼 이송 기법의 일반적인 형식은 다음과 같습니다.
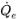은 현재 시간 단계에서 흐름 필드를 기반으로 계산됩니다. 면 값 αq,e는 셀 중심 값 αq,P,αq,E 및 인접 셀 P 및 E의 구배(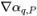, 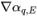)를 기반으로 근사치를 구합니다. 패시브 스칼라 방정식처럼 이송 기법의 일반적인 형식은 다음과 같습니다.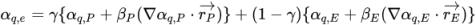
방정식 2.145
매개 변수 γ, βP 및 βE에 대한 서로 다른 값 및 부피 분율 구배를 계산하는 기법을 사용하여 부피 분율 방정식에 대해 네 가지 이송 기법인 1차 상류 이송(First-Order Upwind), 2차 상류 이송(Second-Order Upwind), 중앙 차분(Center Difference), 고분해능(High Resolution)이 전개됩니다.
◦ 시간 기법(Temporal Schemes) - 암시적 시간 기법을 설명하기 위해 다음 표현식에서 방정식 2.144를 일반화할 수 있습니다.
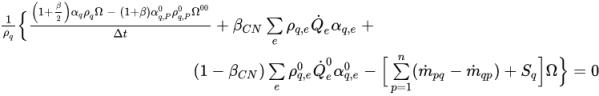
방정식 2.146
위 첨자가 없는 변수가 현재 시간 단계의 값입니다. 위 첨자 0 또는 00이 있는 변수는 이전 시간 단계의 값을 나타냅니다.
매개 변수 β 및 βCN은 0에서 1 사이로 다양하며 시간 기법을 결정합니다. 특히, 위상 부피 분율 방정식의 이산화를 위해 세 가지 시간 기법이 채택됩니다.
▪ 오일러 1차 상류 이송: β = 0, βCN = 1
▪ 3레벨 2차: β = 0, βCN = 1
▪ Crank-Nicolson 방법: β = 0, βCN = 0.6(기본값)
• VOF 명시적 수식
VOF 방정식의 해를 구하는 데 명시적 수식이 사용되는 경우 현재 시간 단계의 위상 부피 분율이 이전 시간 단계의 알려진 수량을 기반으로 직접 계산됩니다. 따라서 VOF 명시적 수식에는 각 시간 단계 동안 방정식 2.144에 대한 반복적 솔루션이 필요하지 않습니다. 그러나 나머지 운송 방정식은 암시적으로 해를 구하기 때문에 부피 분율 계산에 대한 시간 단계는 일반적으로 다른 운송 방정식에 대한 시간 단계보다 더 작습니다. 명시적 VOF 수식에 대한 서브 시간 단계를 결정해야 하며, 이는 자동으로 계산되거나 Creo Flow Analysis에서 제공할 수 있습니다.
명시적 수식을 사용하는 경우 이산화된 위상 부피 분율 방정식의 수식은 다음과 같습니다.
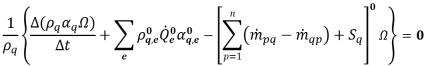
방정식 2.147
여기서 이송 항과 소스 항 모두 이전 시간 단계의 알려진 양을 기반으로 계산됩니다. 체적 유속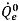 
은 암시적 수식에서 
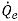과 동일하게 계산됩니다. 평면 부피 분율 
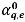는 네 가지 이송 기법인 1차 상류 이송(First-Order Upwind), 2차 상류 이송(Second-Order Upwind), 중앙 차분(Center Difference), 고분해능(High Resolution) 중 하나를 사용하여 추정할 수 있습니다.
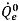은 암시적 수식에서 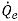과 동일하게 계산됩니다. 평면 부피 분율 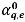는 네 가지 이송 기법인 1차 상류 이송(First-Order Upwind), 2차 상류 이송(Second-Order Upwind), 중앙 차분(Center Difference), 고분해능(High Resolution) 중 하나를 사용하여 추정할 수 있습니다.Creo Flow Analysis는 명시적 시간 마칭 기법에 대해 다음 세 가지 알고리즘을 제공합니다.
• 1차 오일러(Euler) 명시적 - 부피 분율 방정식이 다음과 같이 이산화됩니다.
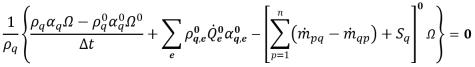
방정식 2.148
• 2차 Runge-Kutta - 다음 함수를 도입합니다.
방정식 2.149
방정식 2.147이 다음과 같이 다시 작성됩니다.
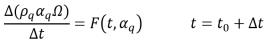
방정식 2.150
그러면 2차 Runge-Kutta 명시적 기법의 형식이 다음과 같습니다.
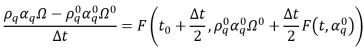
방정식 2.151
• 4차 Runge-Kutta - 위상 q 부피 분율 방정식의 경우 4차 Runge-Kutta 명시적 기법의 형식은 다음과 같습니다.
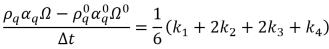
방정식 2.152
여기서 각 항목은 다음을 나타냅니다.
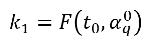
방정식 2.153
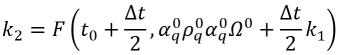
방정식 2.154
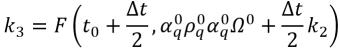
방정식 2.155
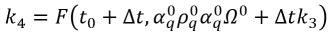
방정식 2.156