오일러 모델 및 지배 방정식
이 단원에서는 VOF(유체 부피) 및 혼합물 다상 모델, 터뷸런스 모델링 및 다상 흐름의 경계 모델링에 대한 지배 방정식을 설명합니다.
일반 다상 지배 방정식
오일러-오일러 접근 방식에서 다상 시스템의 서로 다른 위상 또는 컴포넌트는 동일한 흐름 압력을 공유하는, 매우 정확히 상호 관통하는 연속체로 간주됩니다. 물리적 공간 또는 부피를 모든 위상에서 공유하므로 위상 운송을 설명하기 위해 위상 부피 분율이라는 개념이 도입되었습니다. 위상 부피 분율은 공간과 시간의 연속 함수로 간주되며 해당 합계는 1입니다. 보존 법칙은 이론적 또는 경험적 구성 관계식으로 종결되는 지배 방정식 세트를 파생하기 위해 각 위상에 적용됩니다. 오일러-오일러 접근 방식에서 주기적으로 사용되는 두 가지 유형의 모델은 다음과 같습니다.
• 비균질 또는 오일러 다유체 모델 - 운동량, 에너지, 터뷸런스, 화학종 및 부피 분율 방정식의 위상을 포함하여 각 위상에 대한 지배 방정식의 해를 직접 구합니다. 위상 간 상호 작용, 운동량, 질량, 화학종 및 열의 간기 운송이 물리적 서브모델에 의해 모델링됩니다.
qth 위상에 일반 위상 스칼라인 ϕq, q를 사용하면 위상 q에 대한 일반화된 방정식의 형식은 다음과 같습니다.
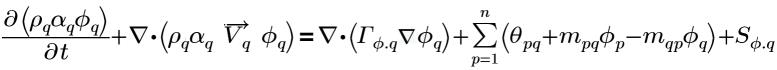
방정식 2.54
여기서 각 항목은 다음을 나타냅니다.
ρq | q 밀도 |
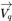 | 속도 |
Sϕq | 소스 항 |
Tϕq | 확산 계수 |
αq | qth 위상의 부피 분율 |
그리고 ϕq는 다상 시스템에서의 종속 변수를 나타냅니다.
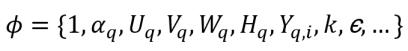
방정식 2.55
여기서 각 항목은 다음을 나타냅니다.
Uq, Vq, Wq | 위상 속도 컴포넌트 |
Hq | 위상 총 엔탈피 |
Yqi | qth 위상에 있는 화학종 "i"의 질량 분율 |
k | 터뷸런스 운동 에너지 |
ε | k-ε 모델에 대한 터뷸런스 운동 에너지 소산율 |
방정식 2.54의 오른쪽에 있는 두 번째 항은 간기 교환을 나타냅니다. 특히, 각 항목은 다음을 나타냅니다.
p | pth 위상 |
n | 다상 시스템의 위상 수 |
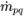 | qth 위상에서 pth 위상으로의 질량 전달 |
θpq | 운동량, 에너지 및 화학종을 포함하는 운송 양의 직접 위상 교환 |
간기 화학종, 질량, 운동량 및 열 교환에 대한 서브모델을 사용하면 여기서 일반화된 운송 방정식에서 흐름 지배 방정식의 전체 세트를 파생할 수 있습니다.
• 균질 다상 모델 - 비균질 모델에 대한 간단하고 경제적인 대체 모델입니다. 균질 모델링 접근 방식은 흐름, 에너지 및 터뷸런스의 위상 지배 방정식의 평균을 내서 혼합물 운송 방정식 세트를 구하는 반면 위상 부피 분율의 해를 계속 구합니다. 혼합물 스칼라 ϕm의 경우 일반화된 지배 방정식의 표현식은 다음과 같습니다.
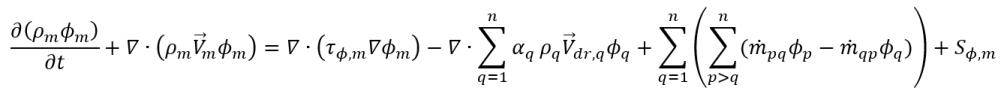
방정식 2.56
여기서 각 항목은 다음을 나타냅니다.
m | 위상 혼합물 |
m을 사용하는 모든 변수 | 혼합물 또는 위상 평균 값 |
그리고 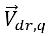 는 위상 q 속도와 혼합물 속도 간의 차이입니다.
는 위상 q 속도와 혼합물 속도 간의 차이입니다.
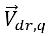 는 위상 q 속도와 혼합물 속도 간의 차이입니다.
는 위상 q 속도와 혼합물 속도 간의 차이입니다.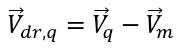
균질 다상 모델은 간기 운송 비율이 큰 오일러-오일러 다상 흐름의 제한 케이스입니다. 기본적으로 모든 위상이 동일한 압력 필드를 공유한다고 가정합니다. 이 가정과 함께 균질 모델은 추가로 모든 위상이 공통 속도, 온도 및 터뷸런스 필드를 공유한다고 가정하여 전체 비균질 오일러 다유체 모델을 단순화합니다. 이 접근 방식은 간단하게 구현되고 경제적으로 계산할 수 있으므로 전체 오일러 다유체 모델의 좋은 대체 방법입니다. 물리적으로 운동량 및 에너지 방정식에서 간기 교환 모델 필요 없이, 균질 모델은 자유 표면 흐름(VOF), 캐비테이션 또는 기타 고혼합 다상 흐름과 같은 경우에 완전 다유체 모델처럼 작동할 수 있습니다.
Creo Flow Analysis에서 현재 다상 모듈은 균질 모델링 접근 방식만 채택합니다. 자유 표면 흐름(유체 부피 모델) 및 균일 액체-기체 2상 흐름(혼합물 모델)을 모델링할 때 특히 주의해야 합니다. 원칙적으로 n상 흐름에 모델링 기능을 적용할 수 있습니다.
VOF 및 혼합물 다상 모델
VOF(유체 부피) 및 혼합물 다상 모델은 균질 모델링 접근 방식을 사용합니다. 각 위상에 있는 부피 분율의 수송 방정식은 방정식 2.54에서 구합니다. 혼합물 운동량 및 에너지에 대한 지배 방정식은 방정식 2.56과 질량, 운동량 및 에너지 보존 법칙을 사용하여 파생됩니다. 지배 방정식 세트는 이 단원에 나와 있습니다.
• 위상 q 부피 분율 방정식
방정식 2.54에서 ϕq=1을 설정하여 위상 q 부피 분율 방정식을 구합니다.
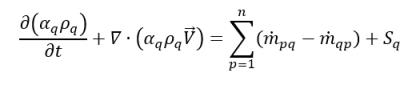
방정식 2.57
여기서 질량 교환 속도 항인 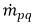 및
및 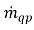 는 각각 위상 q에 대한 소스 및 싱크의 크기를 나타냅니다. 간기 질량 전달 프로세스에서는 이 두 항 중 하나가 일반적으로 0입니다. 다음 예를 참조하십시오.
는 각각 위상 q에 대한 소스 및 싱크의 크기를 나타냅니다. 간기 질량 전달 프로세스에서는 이 두 항 중 하나가 일반적으로 0입니다. 다음 예를 참조하십시오.
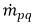 및
및 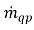 는 각각 위상 q에 대한 소스 및 싱크의 크기를 나타냅니다. 간기 질량 전달 프로세스에서는 이 두 항 중 하나가 일반적으로 0입니다. 다음 예를 참조하십시오.
는 각각 위상 q에 대한 소스 및 싱크의 크기를 나타냅니다. 간기 질량 전달 프로세스에서는 이 두 항 중 하나가 일반적으로 0입니다. 다음 예를 참조하십시오.증발 프로세스에서 액체 위상 q 질량 손실은 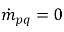 및
및 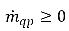 이며, 증기 위상은
이며, 증기 위상은 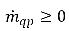 및
및 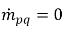 입니다.
입니다.
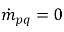 및
및 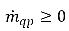 이며, 증기 위상은
이며, 증기 위상은 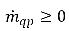 및
및 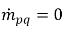 입니다.
입니다.n상 시스템의 경우 위상 부피 분율의 합계는 물리적 제약 조건을 충족합니다.
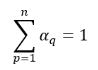
방정식 2.58
또는 총 질량 보존:
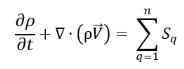
방정식 2.59
여기서 혼합물 양이 다음과 같이 정의됩니다.
◦ 부피-평균 혼합물 밀도
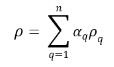
방정식 2.60
◦ 질량-평균 혼합물 속도
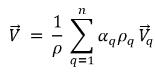
방정식 2.61
• 혼합물 운동량 방정식 - 시스템에 있는 모든 위상에 대한 개별 운동량 방정식을 합해서 구합니다. 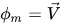 을 설정하여 방정식 2.56부터 다음을 갖습니다.
을 설정하여 방정식 2.56부터 다음을 갖습니다.
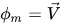 을 설정하여 방정식 2.56부터 다음을 갖습니다.
을 설정하여 방정식 2.56부터 다음을 갖습니다.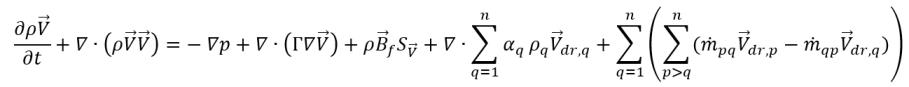
방정식 2.62
여기서 혼합물 양이 다음과 같이 정의됩니다.
◦ 부피-평균 혼합물 점도:

방정식 2.63
방정식 2.62의 확산 계수 Γ는 혼합물 역학 점도 μ 및 터뷸런스 점도 μt를 사용하여 계산됩니다. 오른쪽 마지막에 있는 두 항은 직접 운동량 전달 및 질량-전달 유도 운동량 교환을 나타냅니다. 이는 다음과 같이 정의된 위상 드리프트 속도(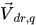 )에 의해 결정됩니다.
)에 의해 결정됩니다.
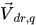 )에 의해 결정됩니다.
)에 의해 결정됩니다.
방정식 2.69
균질 접근 방식에서는 대수 모델을 사용하여 이 드리프트 속도를 모델링할 수 있습니다. 그러나 현재 VOF 및 혼합물 모델에서는 위상 간 슬립이 없는 것으로 가정됩니다.
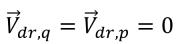
따라서 운동량 교환 항은 모두 0입니다.
◦ 혼합물 에너지 방정식
속도 슬립 없는 혼합물에 대한 에너지 방정식의 형식은 다음과 같습니다.
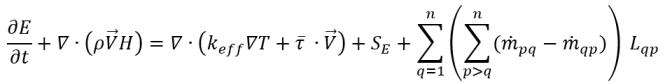
방정식 2.70
여기서 혼합물 변수가 다음과 같이 정의됩니다.
▪ 부피-평균 열 전도성
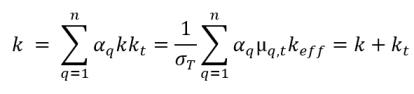
방정식 2.71
▪ 질량-평균 혼합물 에너지 및 엔탈피
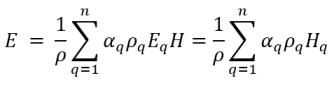
방정식 2.72
혼합물 에너지 방정식 2.70에서는 점성 가열 항(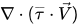 )이 단일 위상 흐름처럼 계산됩니다. 그리고 SE가 전체 외부/사용자 열원입니다.
)이 단일 위상 흐름처럼 계산됩니다. 그리고 SE가 전체 외부/사용자 열원입니다.
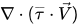 )이 단일 위상 흐름처럼 계산됩니다. 그리고 SE가 전체 외부/사용자 열원입니다.
)이 단일 위상 흐름처럼 계산됩니다. 그리고 SE가 전체 외부/사용자 열원입니다.오른쪽 마지막 항은 질량 전달에 의해 발생하는 계면 열 전달입니다. 위상이 동일한 온도를 공유한다는 가정하에서 Lgp는 풀이된 에너지 방정식의 Hq 및 Hp 정의에 따라 달라집니다.
열(Heat) 모듈에서 설명한 대로 재료의 정적 엔탈피는 두 부분인 표준 상태 기준 엔탈피와 현열 엔탈피로 구성됩니다. 위상 q가 액체이고 위상 p가 증기라는 가정하에서 위상 전체 정적 엔탈피는 다음과 같습니다.
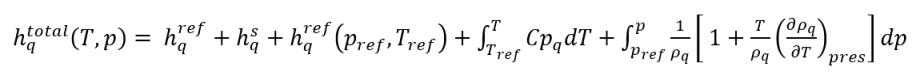
방정식 2.73
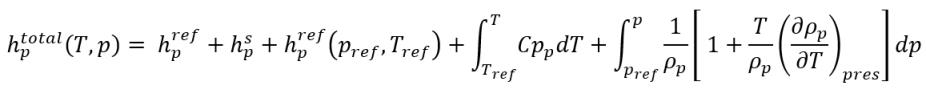
방정식 2.74
여기서 각 항목은 다음을 나타냅니다.
pref | 기준 압력 |
Tref | 기준 온도 |
hq,ref | 위상 q 표준 상태 기준 엔탈피 |
hp,ref | 위상 p 표준 상태 기준 엔탈피 |
이 두 기준 엔탈피의 차이는 다음과 같습니다.
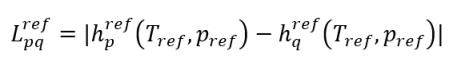
방정식 2.75
기준 온도 Tref 및 압력 pref에서의 잠열입니다.
▪ 표준 기준 엔탈피 포함:
방정식 2.70에서 엔탈피 H가 전체 혼합물 엔탈피인 경우 다음과 같습니다.
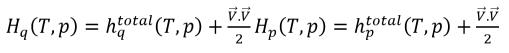
방정식 2.76
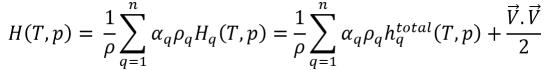
방정식 2.77
이 경우 위상 생성 엔탈피 또는 잠열 Lpq로 인한 차이가 이미 에너지 방정식에 포함되어 있습니다. 수량이 0으로 설정됩니다.
Lpq=0
그리고 질량 전달로 인한 열 전달, 혼합물 에너지 방정식에서 방정식 2.70의 오른쪽 마지막 항이 0입니다.
▪ 표준 기준 엔탈피 제외:
CFD 풀이 시스템에서는 전체 엔탈피의 해를 직접 구하지 않습니다. 대신 포화 온도에 상대적인 현열 엔탈피만 풀이된 엔탈피 및 내부 에너지에 포함됩니다.
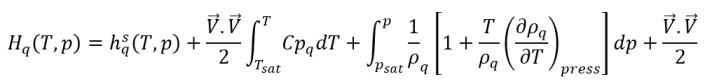
방정식 2.79
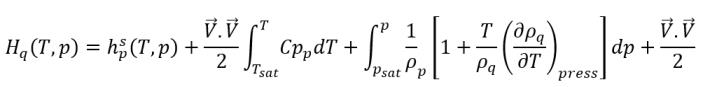
방정식 2.80
그러면 Lpq는 0이 아닙니다. 잠열이어야 합니다.
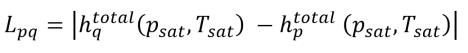
방정식 2.81
여기서 각 항목은 다음을 나타냅니다.
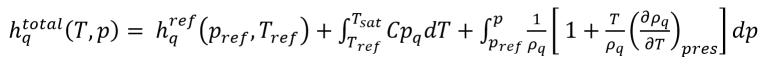
방정식 2.82
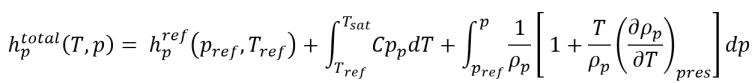
방정식 2.83
Creo Flow Analysis에서는 기본적으로 표준 상태 기준 엔탈피가 자동으로 고려됩니다. 사용자가 입력할 필요가 없습니다.
터뷸런스 모델
• 혼합물 k-ε 터뷸런스 모델
VOF(유체 부피) 및 혼합물 다상 모델에서 위상 혼합물에 터뷸런스가 주는 영향은 단상 터뷸런스 모델의 확장을 사용하여 계산됩니다. Creo Flow Analysis에서는 터뷸런스(Turbulence) 모듈에 설명된 터뷸런스 모델 및 벽 근처 처리가 다상 흐름으로 확장됩니다. 혼합물 흐름 양을 사용하는 표준 및 RNG k–ε 모델의 일반적인 형식은 단상 터뷸런스 모델의 경우와 동일합니다.
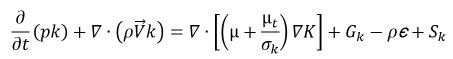
방정식 2.84
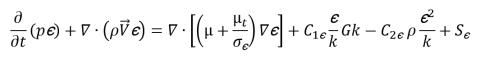
방정식 2.85
여기서 혼합물 밀도 ρ, 속도 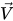 및 분자 점도 μ 각각 방정식 2.60, 방정식 2.61 및 방정식 2.63의 관계식을 사용하여 각 위상 값에서 계산됩니다. Sk 및 Sε은 가능한 외부 소스와 사용자 소스 및 위상 상호 작용 소스를 모두 포함합니다. 혼합물에 대한 터뷸런스 점도 μt는 다음 표현식에서 직접 계산됩니다.
및 분자 점도 μ 각각 방정식 2.60, 방정식 2.61 및 방정식 2.63의 관계식을 사용하여 각 위상 값에서 계산됩니다. Sk 및 Sε은 가능한 외부 소스와 사용자 소스 및 위상 상호 작용 소스를 모두 포함합니다. 혼합물에 대한 터뷸런스 점도 μt는 다음 표현식에서 직접 계산됩니다.
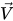 및 분자 점도 μ 각각 방정식 2.60, 방정식 2.61 및 방정식 2.63의 관계식을 사용하여 각 위상 값에서 계산됩니다. Sk 및 Sε은 가능한 외부 소스와 사용자 소스 및 위상 상호 작용 소스를 모두 포함합니다. 혼합물에 대한 터뷸런스 점도 μt는 다음 표현식에서 직접 계산됩니다.
및 분자 점도 μ 각각 방정식 2.60, 방정식 2.61 및 방정식 2.63의 관계식을 사용하여 각 위상 값에서 계산됩니다. Sk 및 Sε은 가능한 외부 소스와 사용자 소스 및 위상 상호 작용 소스를 모두 포함합니다. 혼합물에 대한 터뷸런스 점도 μt는 다음 표현식에서 직접 계산됩니다.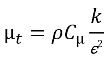
방정식 2.86
터뷸런스 운동 에너지의 생산은 혼합물 터뷸런스 점도 및 속도 구배를 기반으로 계산됩니다.
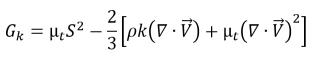
방정식 2.87
여기서 S는 평균 혼합물 변형률 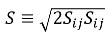 의 탄성 계수입니다.
의 탄성 계수입니다.
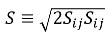 의 탄성 계수입니다.
의 탄성 계수입니다.위상 q에 대한 터뷸런스 점도는 다음과 같이 계산될 수 있습니다.
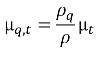
방정식 2.87
• 터뷸런스 확산의 효과
다상 터뷸런스 흐름의 경우 순간 계면 드래그 항의 평균을 낼 때 터뷸런스 분산 힘(위상 확산의 해당 힘과 같이 작동)이 발생합니다. 비균질 오일러 다유체 모델은 대개 이 터뷸런스 효과를 추가 간기 힘으로 처리하며 이러한 힘은 위상 운동량 방정식에서 위상 부피 분율의 구배에 의해 결정됩니다. 그러나 이 터뷸런스 효과는 이를 위상 부피 분율 방정식에서 터뷸런스 확산 항으로 직접 고려해서 모델링될 수도 있습니다. 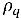 을 나누고 모든 소스를
을 나누고 모든 소스를 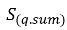 (간기 질량 전달 및 외부 질량 소스의 합)으로 그룹화하면 터뷸런스 흐름에서 위상 q 부피 분율에 대한 다음과 같은 지배 방정식이 생성됩니다.
(간기 질량 전달 및 외부 질량 소스의 합)으로 그룹화하면 터뷸런스 흐름에서 위상 q 부피 분율에 대한 다음과 같은 지배 방정식이 생성됩니다.
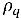 을 나누고 모든 소스를
을 나누고 모든 소스를 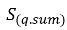 (간기 질량 전달 및 외부 질량 소스의 합)으로 그룹화하면 터뷸런스 흐름에서 위상 q 부피 분율에 대한 다음과 같은 지배 방정식이 생성됩니다.
(간기 질량 전달 및 외부 질량 소스의 합)으로 그룹화하면 터뷸런스 흐름에서 위상 q 부피 분율에 대한 다음과 같은 지배 방정식이 생성됩니다.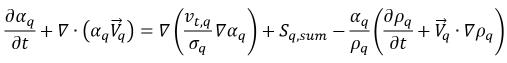
여기서 오른쪽에 있는 첫 번째 항은 위상 q의 터뷸런스 확산 항으로, 총 질량 보존의 법칙을 충족하도록 다음 제약 조건을 만족해야 합니다.
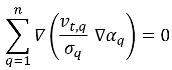
터뷸런스 확산 항은 대개 옵션으로 구현됩니다. 이는 기본적으로 포함되지 않습니다.
다상 경계의 모델링
VOF(유체 부피) 및 혼합물 다상 모델에서 흐름 및 에너지 방정식에 대한 경계 조건은 단상 흐름에서의 경계 조건과 동일합니다. 이는 흐름(Flow) 및 열(Heat) 모듈에 설명되어 있습니다. 위상 부피 분율의 경우 고정 값 및 0 구배가 다음에 적용됩니다.
• n상 유입구 경계
(n–1) 위상의 경우 유입구 부피 분율은 미리 결정되며, nth 위상은 물리적 제약 조건을 사용하여 구합니다.
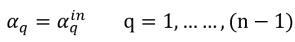
방정식 2.88
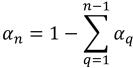
방정식 2.89
그리고 각 위상의 부피 분율은 음수가 아니어야 합니다.
• 배출구/대칭/벽 경계
(n–1) 위상의 경우 모든 배출구, 대칭 및 벽 경계에 0 구배 조건이 적용되며, nth 위상은 물리적 제약 조건을 사용하여 구합니다.
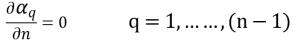
방정식 2.90
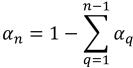
방정식 2.91
위의 지배 방정식, 터뷸런스 모델 및 경계 조건이 균질 VOF 및 혼합물 다상 모델의 기초가 됩니다. 외부 소스 또는 사용자 소스 항 및 간기 질량 전달 없이, 이러한 항목은 닫힌 방정식 시스템이며 압력 기반 유한 부피 다상 풀이 시스템을 사용하여 수학적으로 해를 구합니다. 여러 실제 적용 시 VOF 모델의 표면 장력과 같은 특정 서브모델 및 간기 질량 전달은 해당 물리적 현상과 프로세스를 정확하게 캡처하는 데 필수적입니다. 서브모델을 외부 소스 또는 사용자 소스로 묶는 대신 기본 제공 모델에 직접 포함하는 것이 좋습니다.