ODE 풀이 시스템
각각 경계 및 볼륨의 1-DOF 전환 및 회전을 제어하는 ODE(상미분 방정식) 방정식 2.432 및 방정식 2.444는 Creo Flow Analysis에서 수치적으로 풀립니다. 특히, 다시 메쉬에 대한 경계 및 볼륨 이동 및 변위를 계산하기 위해 다음 시간 마칭 기법이 사용되어 ODE 방정식인 스티프(Stiff), 오일러 및 런지-쿠타 명시적 풀이 시스템을 통합합니다.
1-DOF 변환 방정식의 통합
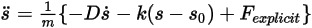
방정식 2.455
여기서 명시적으로 계산된 힘 항 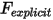 은 다음과 같습니다.
은 다음과 같습니다.
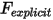 은 다음과 같습니다.
은 다음과 같습니다.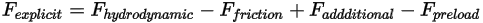
방정식 2.456
주어진 초기 및 경계 조건에서는 명시적 시간 마칭 기법을 사용하여 방정식 2.455를 통합하여 솔리드 바디의 변위를 구합니다. 시간에 따른 단계 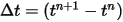 에서 일반 수식은 다음과 같습니다.
에서 일반 수식은 다음과 같습니다.
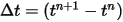 에서 일반 수식은 다음과 같습니다.
에서 일반 수식은 다음과 같습니다.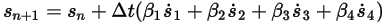
방정식 2.457
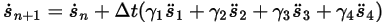
방정식 2.458
여기서 가중 계수의 합은 1입니다.
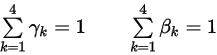
방정식 2.459
가중 계수를 선택하면 서로 다른 체계가 파생됩니다. 예를 들어 오일러 및 런지-쿠타 명시적 체계는 다음과 같습니다.
• 오일러 명시적 풀이 시스템(첫 번째)
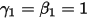 및
및 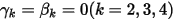 을 사용하는 경우 오일러 명시적 체계는 다음과 같습니다.
을 사용하는 경우 오일러 명시적 체계는 다음과 같습니다.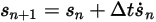
방정식 2.460
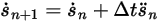
방정식 2.461
• 런지-쿠타 명시적 풀이 시스템
런지-쿠타 풀이 시스템은 다음과 같은 두 번째 및 네 번째 명시적 체계입니다.
◦ 두 번째 체계
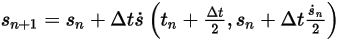
방정식 2.462
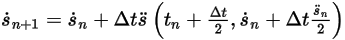
방정식 2.463
◦ 네 번째 체계
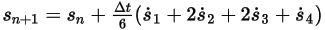
방정식 2.464
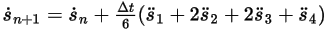
방정식 2.465
여기서 각 항목은 다음을 나타냅니다.

방정식 2.466

방정식 2.467

방정식 2.468

방정식 2.469
• 스티프(Stiff) 풀이 시스템(명시적)
표준 오일러 및 런지-쿠타 체계 외에도 Creo Flow Analysis에서는 변환 1-DOF ODE 방정식을 통합하는 스티프(Stiff) 풀이 시스템을 개발했습니다. 이는 솔리드 바디의 역학 동작에 대한 기본 방법입니다.
1-DOF 회전 방정식의 통합
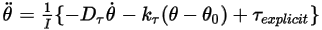
방정식 2.470
여기서 명시적으로 계산된 토크 항 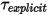 은 다음과 같습니다.
은 다음과 같습니다.
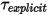 은 다음과 같습니다.
은 다음과 같습니다.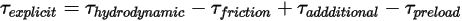
방정식 2.471
주어진 초기 및 경계 조건에서는 명시적 시간 마칭 체계를 사용하여 방정식 2.470를 통합하여 회전 각도를 구합니다. 시간에 따른 단계 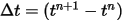 에서 일반 수식은 다음과 같습니다.
에서 일반 수식은 다음과 같습니다.
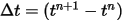 에서 일반 수식은 다음과 같습니다.
에서 일반 수식은 다음과 같습니다.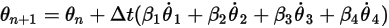
방정식 2.472
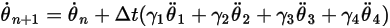
방정식 2.473
여기서 가중 계수의 합은 1입니다.
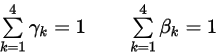
방정식 2.474
가중 계수를 선택하면 서로 다른 수치 체계가 쉽게 파생됩니다. 다시 오일러 및 런지-쿠타 명시적 체계가 아래에 제공됩니다.
• 오일러 명시적 풀이 시스템(첫 번째)
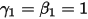 및
및 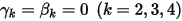 을 사용하는 경우 오일러 명시적 체계는 다음과 같습니다.
을 사용하는 경우 오일러 명시적 체계는 다음과 같습니다.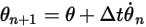
방정식 2.475
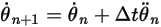
방정식 2.476
• 런지-쿠타 명시적 풀이 시스템
런지-쿠타 풀이 시스템은 아래에 제공된 두 번째 및 네 번째 명시적 체계입니다.
◦ 두 번째 체계
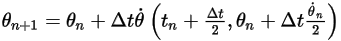
방정식 2.477
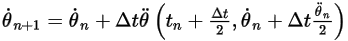
방정식 2.478
◦ 네 번째 체계
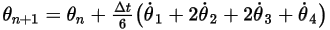
방정식 2.479
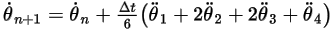
방정식 2.480
여기서 각 항목은 다음을 나타냅니다.

방정식 2.481

방정식 2.482

방정식 2.483

방정식 2.484
• 스티프(Stiff) 풀이 시스템(명시적)
표준 오일러 및 런지-쿠타 체계 외에도 Creo Flow Analysis에서는 1-DOF 회전 ODE 방정식 2.444를 통합하는 스티프(Stiff) 풀이 시스템을 개발했습니다. 이는 솔리드 바디의 역학 동작에 대한 기본 방법입니다.
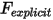 으로 그룹화하는 경우 동작의 1-DOF 변환 방정식을 다음 형식으로 다시 작성합니다.
으로 그룹화하는 경우 동작의 1-DOF 변환 방정식을 다음 형식으로 다시 작성합니다.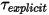 으로 그룹화하는 경우 동작의 1-DOF 회전 방정식
으로 그룹화하는 경우 동작의 1-DOF 회전 방정식