강체의 동작
시뮬레이션에서 솔리드 객체의 서피스는 일반적으로 흐름 도메인의 벽 경계입니다. 솔리드 객체나 서피스가 역학 및 기계적 힘과 열 효과의 영향을 받을 때 알짜 힘의 불균형으로 인해 바디가 이동 및 변형될 수 있습니다. 솔리드 객체는 흐름 시뮬레이션에서 강체로 간주되는 경우가 많습니다. 따라서 힘 불균형의 영향을 받는 솔리드 객체의 경우 해당 객체가 변형 없이 선형 이동(변환)과 각도상 이동(회전) 중 하나를 수행하거나 둘 다를 수행할 수 있다고 가정합니다. 그러나 CFA 계산 도메인의 경우 경계 이동으로 인해 도메인 변경이 발생할 수 있으며 결과적으로 흐름(Flow) 모듈에 설명된 대로 볼륨 메쉬가 변형될 수 있습니다.
강체의 경우 해당 동작을 제어하는 방정식은 선형 및 각 운동량 보존에서 직접 파생됩니다.
• 선형 운동량(변환)
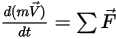
방정식 2.426
• 각 운동량(회전)
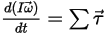
방정식 2.427
방정식 2.426 및 방정식 2.427은 각각 변환(3-DOF) 및 회전(3-DOF)을 위한 세 개의 각도를 포함하는 6개 자유도(6-DOF)가 있는 솔리드 바디의 일반 동작을 제어합니다. Creo Flow Analysis에서는 이 단원에서 설명하는 1-DOF 변환 및 회전만 고려합니다.
1-DOF 변환
솔리드 바디가 단위 벡터 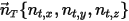 에서 정의한 임의로 지정된 방향에서 선형으로 이동(변경되지 않은 상태 유지)한다는 가정에서 솔리드 바디의 변환 동작은 1 자유도(1-DOF)로 줄어듭니다. 따라서 선형 운동량 보존의 경우 방정식 2.426은 이동 속도와 힘이
에서 정의한 임의로 지정된 방향에서 선형으로 이동(변경되지 않은 상태 유지)한다는 가정에서 솔리드 바디의 변환 동작은 1 자유도(1-DOF)로 줄어듭니다. 따라서 선형 운동량 보존의 경우 방정식 2.426은 이동 속도와 힘이 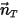 을 기준으로 표현되므로 이동 방향에 따라 스칼라 방정식이 됩니다.
을 기준으로 표현되므로 이동 방향에 따라 스칼라 방정식이 됩니다.
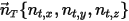 에서 정의한 임의로 지정된 방향에서 선형으로 이동(변경되지 않은 상태 유지)한다는 가정에서 솔리드 바디의 변환 동작은 1 자유도(1-DOF)로 줄어듭니다. 따라서 선형 운동량 보존의 경우 방정식 2.426은 이동 속도와 힘이
에서 정의한 임의로 지정된 방향에서 선형으로 이동(변경되지 않은 상태 유지)한다는 가정에서 솔리드 바디의 변환 동작은 1 자유도(1-DOF)로 줄어듭니다. 따라서 선형 운동량 보존의 경우 방정식 2.426은 이동 속도와 힘이 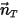 을 기준으로 표현되므로 이동 방향에 따라 스칼라 방정식이 됩니다.
을 기준으로 표현되므로 이동 방향에 따라 스칼라 방정식이 됩니다.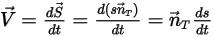
방정식 2.428
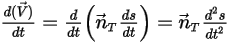
방정식 2.429
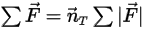
방정식 2.430
여기서 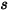 은 이동 방향
은 이동 방향 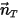 에 따라 솔리드 바디에 대한 관심 지점에서의 위치 벡터
에 따라 솔리드 바디에 대한 관심 지점에서의 위치 벡터 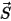 의 강도입니다. 카티시안 좌표계에서는 다음을 사용할 수 있습니다.
의 강도입니다. 카티시안 좌표계에서는 다음을 사용할 수 있습니다.
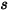 은 이동 방향
은 이동 방향 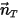 에 따라 솔리드 바디에 대한 관심 지점에서의 위치 벡터
에 따라 솔리드 바디에 대한 관심 지점에서의 위치 벡터 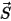 의 강도입니다. 카티시안 좌표계에서는 다음을 사용할 수 있습니다.
의 강도입니다. 카티시안 좌표계에서는 다음을 사용할 수 있습니다.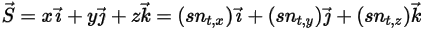
방정식 2.431
솔리드 바디의 질량이 일정하게 유지되고 힘 항을 확장하여 바디에 적용된 모든 힘을 명시적으로 포함하는 경우 다음과 같은 스칼라 선형 운동량 방정식을 사용할 수 있습니다.
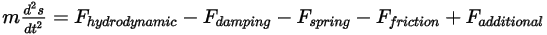
방정식 2.432
오른쪽에 있는 힘은 다음을 나타냅니다.
• 동유체력  - 압력 및 전단력으로 구성됩니다. 이러한 힘은 흐름과 접촉하는 솔리드 바디의 서피스와 유체 흐름 간의 상대적 동작에 의해 발생합니다. 압력 및 전단력은 흐름 솔루션(출력 수량)에서 구합니다.
- 압력 및 전단력으로 구성됩니다. 이러한 힘은 흐름과 접촉하는 솔리드 바디의 서피스와 유체 흐름 간의 상대적 동작에 의해 발생합니다. 압력 및 전단력은 흐름 솔루션(출력 수량)에서 구합니다.
 - 압력 및 전단력으로 구성됩니다. 이러한 힘은 흐름과 접촉하는 솔리드 바디의 서피스와 유체 흐름 간의 상대적 동작에 의해 발생합니다. 압력 및 전단력은 흐름 솔루션(출력 수량)에서 구합니다.
- 압력 및 전단력으로 구성됩니다. 이러한 힘은 흐름과 접촉하는 솔리드 바디의 서피스와 유체 흐름 간의 상대적 동작에 의해 발생합니다. 압력 및 전단력은 흐름 솔루션(출력 수량)에서 구합니다.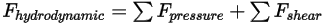
방정식 2.433
• 댐핑 힘 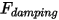 - 마찰 댐핑 효과에 의해 발생하는 억제 힘입니다. 이러한 힘은 솔리드 객체의 동작과 사용자 정의 댐핑 계수
- 마찰 댐핑 효과에 의해 발생하는 억제 힘입니다. 이러한 힘은 솔리드 객체의 동작과 사용자 정의 댐핑 계수 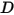 에 의해 결정됩니다.
에 의해 결정됩니다.
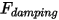 - 마찰 댐핑 효과에 의해 발생하는 억제 힘입니다. 이러한 힘은 솔리드 객체의 동작과 사용자 정의 댐핑 계수
- 마찰 댐핑 효과에 의해 발생하는 억제 힘입니다. 이러한 힘은 솔리드 객체의 동작과 사용자 정의 댐핑 계수 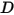 에 의해 결정됩니다.
에 의해 결정됩니다.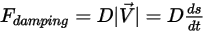
방정식 2.434
• 스프링력 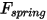 - 스프링
- 스프링 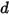 , 스프링 상수
, 스프링 상수 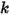 및 스프링 예비 하중 힘
및 스프링 예비 하중 힘 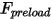 의 변위에 따라 달라집니다.
의 변위에 따라 달라집니다.
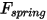 - 스프링
- 스프링 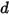 , 스프링 상수
, 스프링 상수 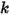 및 스프링 예비 하중 힘
및 스프링 예비 하중 힘 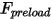 의 변위에 따라 달라집니다.
의 변위에 따라 달라집니다.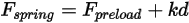
방정식 2.435
여기서 스프링 변위 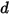 은 다음과 같이 정의됩니다.
은 다음과 같이 정의됩니다.
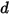 은 다음과 같이 정의됩니다.
은 다음과 같이 정의됩니다.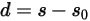
방정식 2.436
여기서 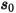 은 이전 위치
은 이전 위치 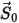 에서의 위치 벡터
에서의 위치 벡터 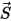 의 강도입니다.
의 강도입니다.
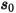 은 이전 위치
은 이전 위치 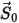 에서의 위치 벡터
에서의 위치 벡터 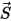 의 강도입니다.
의 강도입니다.• 마찰력 - 역학 시스템에서의 마찰 효과를 계산하기 위해 접촉 마찰 모델이 채택됩니다. 마찰력 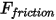 은 다음과 같이 모델링됩니다.
은 다음과 같이 모델링됩니다.
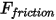 은 다음과 같이 모델링됩니다.
은 다음과 같이 모델링됩니다.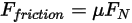
방정식 2.437
여기서 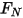 은 관심 솔리드 서피스에 적용된 접촉력의 수직 컴포넌트입니다. 마찰 계수
은 관심 솔리드 서피스에 적용된 접촉력의 수직 컴포넌트입니다. 마찰 계수 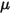 의 경우 정적 마찰 계수
의 경우 정적 마찰 계수 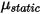 및 슬라이딩 마찰 계수
및 슬라이딩 마찰 계수 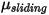 이 각각 고정 바디와 이동 바디에 대해 추가로 도입됩니다.
이 각각 고정 바디와 이동 바디에 대해 추가로 도입됩니다.
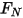 은 관심 솔리드 서피스에 적용된 접촉력의 수직 컴포넌트입니다. 마찰 계수
은 관심 솔리드 서피스에 적용된 접촉력의 수직 컴포넌트입니다. 마찰 계수 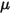 의 경우 정적 마찰 계수
의 경우 정적 마찰 계수 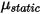 및 슬라이딩 마찰 계수
및 슬라이딩 마찰 계수 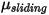 이 각각 고정 바디와 이동 바디에 대해 추가로 도입됩니다.
이 각각 고정 바디와 이동 바디에 대해 추가로 도입됩니다.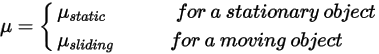
방정식 2.438
• 추가 힘 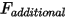 - 추가 사용자 지정 힘으로 추가됩니다.
- 추가 사용자 지정 힘으로 추가됩니다.
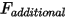 - 추가 사용자 지정 힘으로 추가됩니다.
- 추가 사용자 지정 힘으로 추가됩니다.1-DOF 회전
임의 회전 축이 점(축 중심)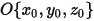 및 방향 단위 벡터
및 방향 단위 벡터 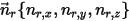 에 의해 정의되면 축
에 의해 정의되면 축 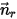 주위의 솔리드 바디 회전도 1-DOF 회전으로 감소합니다. 마찬가지로 각 운동량 보존의 경우 방정식 2.427도 다음과 같이 정의된 탄젠트 방향
주위의 솔리드 바디 회전도 1-DOF 회전으로 감소합니다. 마찬가지로 각 운동량 보존의 경우 방정식 2.427도 다음과 같이 정의된 탄젠트 방향 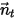 을 따라 스칼라 방정식이 됩니다.
을 따라 스칼라 방정식이 됩니다.
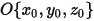 및 방향 단위 벡터
및 방향 단위 벡터 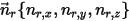 에 의해 정의되면 축
에 의해 정의되면 축 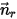 주위의 솔리드 바디 회전도 1-DOF 회전으로 감소합니다. 마찬가지로 각 운동량 보존의 경우 방정식 2.427도 다음과 같이 정의된 탄젠트 방향
주위의 솔리드 바디 회전도 1-DOF 회전으로 감소합니다. 마찬가지로 각 운동량 보존의 경우 방정식 2.427도 다음과 같이 정의된 탄젠트 방향 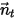 을 따라 스칼라 방정식이 됩니다.
을 따라 스칼라 방정식이 됩니다.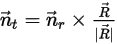
방정식 2.439
여기서 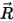 은 축의 중심에서 솔리드 바디의 임의의 점
은 축의 중심에서 솔리드 바디의 임의의 점 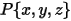 을 가리키는 벡터입니다.
을 가리키는 벡터입니다.
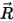 은 축의 중심에서 솔리드 바디의 임의의 점
은 축의 중심에서 솔리드 바디의 임의의 점 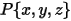 을 가리키는 벡터입니다.
을 가리키는 벡터입니다.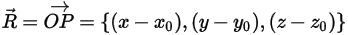
방정식 2.440
점 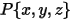 의 각속도 및 토크는 다음과 같이 다시 작성됩니다.
의 각속도 및 토크는 다음과 같이 다시 작성됩니다.
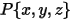 의 각속도 및 토크는 다음과 같이 다시 작성됩니다.
의 각속도 및 토크는 다음과 같이 다시 작성됩니다.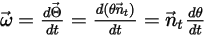
방정식 2.441
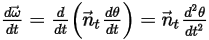
방정식 2.442
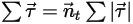
방정식 2.443
여기서 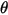 은 시작 또는 참조 위치에 상대적인 점
은 시작 또는 참조 위치에 상대적인 점 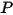 의 회전 각도입니다.
의 회전 각도입니다.
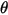 은 시작 또는 참조 위치에 상대적인 점
은 시작 또는 참조 위치에 상대적인 점 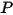 의 회전 각도입니다.
의 회전 각도입니다.관성 모멘트가 일정하게 유지되고 토크 항을 확장하여 회전 바디에 적용된 모든 토크를 명시적으로 포함하는 경우 다음과 같은 스칼라 각 운동량 방정식을 사용할 수 있습니다.
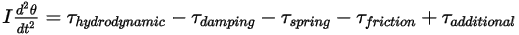
방정식 2.444
오른쪽에 있는 토크 항은 다음과 같이 정의됩니다.
• 동유체 토크 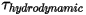 - 압력 및 전단력으로 인한 토크의 조합입니다.
- 압력 및 전단력으로 인한 토크의 조합입니다.
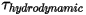 - 압력 및 전단력으로 인한 토크의 조합입니다.
- 압력 및 전단력으로 인한 토크의 조합입니다.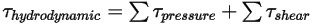
방정식 2.445
• 댐핑 토크 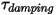 - 회전 속도
- 회전 속도 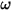 및 사용자 정의 댐핑 계수
및 사용자 정의 댐핑 계수 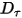 에 따라 달라집니다.
에 따라 달라집니다.
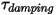 - 회전 속도
- 회전 속도 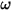 및 사용자 정의 댐핑 계수
및 사용자 정의 댐핑 계수 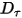 에 따라 달라집니다.
에 따라 달라집니다.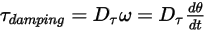
방정식 2.446
• 스프링 토크 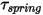 - 변위 각도
- 변위 각도 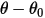 , 사용자 정의 예비 하중 토크
, 사용자 정의 예비 하중 토크 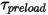 및 비틀림 상수
및 비틀림 상수 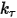 에 따라 달라지는 비틀림에 의해 유도되는 토크입니다.
에 따라 달라지는 비틀림에 의해 유도되는 토크입니다.
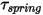 - 변위 각도
- 변위 각도 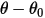 , 사용자 정의 예비 하중 토크
, 사용자 정의 예비 하중 토크 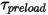 및 비틀림 상수
및 비틀림 상수 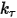 에 따라 달라지는 비틀림에 의해 유도되는 토크입니다.
에 따라 달라지는 비틀림에 의해 유도되는 토크입니다.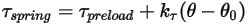
방정식 2.447
여기서 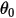 은 참조 각도입니다. 이는 일반적으로 모델을 설정하는 동안의 경계 또는 볼륨의 위치이지만 다른 위치에 해당할 수 있습니다. 예를 들어 제로 각변위에서는 참조 각도
은 참조 각도입니다. 이는 일반적으로 모델을 설정하는 동안의 경계 또는 볼륨의 위치이지만 다른 위치에 해당할 수 있습니다. 예를 들어 제로 각변위에서는 참조 각도 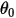 이 초기 각도 위치와 동일하지 않습니다.
이 초기 각도 위치와 동일하지 않습니다.
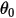 은 참조 각도입니다. 이는 일반적으로 모델을 설정하는 동안의 경계 또는 볼륨의 위치이지만 다른 위치에 해당할 수 있습니다. 예를 들어 제로 각변위에서는 참조 각도
은 참조 각도입니다. 이는 일반적으로 모델을 설정하는 동안의 경계 또는 볼륨의 위치이지만 다른 위치에 해당할 수 있습니다. 예를 들어 제로 각변위에서는 참조 각도 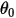 이 초기 각도 위치와 동일하지 않습니다.
이 초기 각도 위치와 동일하지 않습니다.• 마찰 토크 - 접촉에서 두 개의 객체가 이동할 때 발생하는 마찰 힘에 의해 발생하는 토크입니다. 실험에서는 적용된 토크와 관측된 토크 또는 순 토크 간의 차이에 의해 결정됩니다. 이는 접촉 서피스에 적용된 수직항력 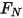 으로 인한 마찰 계수
으로 인한 마찰 계수 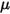 및 접촉 토크에 따라 달라집니다.
및 접촉 토크에 따라 달라집니다.
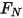 으로 인한 마찰 계수
으로 인한 마찰 계수 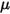 및 접촉 토크에 따라 달라집니다.
및 접촉 토크에 따라 달라집니다.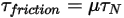
방정식 2.448
여기서 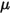 은 방정식 2.438에 정의된 사용자 정의 매개 변수입니다.
은 방정식 2.438에 정의된 사용자 정의 매개 변수입니다.
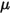 은 방정식 2.438에 정의된 사용자 정의 매개 변수입니다.
은 방정식 2.438에 정의된 사용자 정의 매개 변수입니다.• 추가 토크 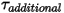 - 추가 사용자 지정 토크용으로 추가되었습니다.
- 추가 사용자 지정 토크용으로 추가되었습니다.
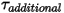 - 추가 사용자 지정 토크용으로 추가되었습니다.
- 추가 사용자 지정 토크용으로 추가되었습니다.바운스 모델
대부분의 경우 솔리드 바디는 제한된 공간(제한된 거리 또는 각도)에서 변환과 회전 중 하나 또는 둘 다를 수행합니다. 즉, 솔리드 바디에 최대 위치와 최소 위치 중 하나 또는 둘 다가 포함됩니다. 예를 들어, 다음 그림과 같이 각도가 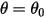 인 원래 위치에서 단순 중력 진자가 해제될 때 해당 질량에 대해 작용하는 복원력으로 인해 진자가 평형 위치에 대해 진동합니다. 평형 위치
인 원래 위치에서 단순 중력 진자가 해제될 때 해당 질량에 대해 작용하는 복원력으로 인해 진자가 평형 위치에 대해 진동합니다. 평형 위치 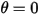 의 한쪽 측면에 대한 최대 각도는 해당 해제 위치
의 한쪽 측면에 대한 최대 각도는 해당 해제 위치 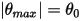 에 따라 달라집니다. 마찰이 없는 경우(무마찰 및 진공 상태) 최대 각도는 변경되지 않은 상태로 유지되고 진자는 동일한 극단적 위치에서 계속 앞뒤로 흔들립니다. 그러나 진자가 대기 중에 있을 때 공기 저항(댐핑) 등으로 인해 최대 스윙 각도가 시간 경과에 따라 감소하여 결국 평형 위치에서 멈춥니다.
에 따라 달라집니다. 마찰이 없는 경우(무마찰 및 진공 상태) 최대 각도는 변경되지 않은 상태로 유지되고 진자는 동일한 극단적 위치에서 계속 앞뒤로 흔들립니다. 그러나 진자가 대기 중에 있을 때 공기 저항(댐핑) 등으로 인해 최대 스윙 각도가 시간 경과에 따라 감소하여 결국 평형 위치에서 멈춥니다.
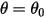 인 원래 위치에서 단순 중력 진자가 해제될 때 해당 질량에 대해 작용하는 복원력으로 인해 진자가 평형 위치에 대해 진동합니다. 평형 위치
인 원래 위치에서 단순 중력 진자가 해제될 때 해당 질량에 대해 작용하는 복원력으로 인해 진자가 평형 위치에 대해 진동합니다. 평형 위치 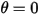 의 한쪽 측면에 대한 최대 각도는 해당 해제 위치
의 한쪽 측면에 대한 최대 각도는 해당 해제 위치 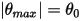 에 따라 달라집니다. 마찰이 없는 경우(무마찰 및 진공 상태) 최대 각도는 변경되지 않은 상태로 유지되고 진자는 동일한 극단적 위치에서 계속 앞뒤로 흔들립니다. 그러나 진자가 대기 중에 있을 때 공기 저항(댐핑) 등으로 인해 최대 스윙 각도가 시간 경과에 따라 감소하여 결국 평형 위치에서 멈춥니다.
에 따라 달라집니다. 마찰이 없는 경우(무마찰 및 진공 상태) 최대 각도는 변경되지 않은 상태로 유지되고 진자는 동일한 극단적 위치에서 계속 앞뒤로 흔들립니다. 그러나 진자가 대기 중에 있을 때 공기 저항(댐핑) 등으로 인해 최대 스윙 각도가 시간 경과에 따라 감소하여 결국 평형 위치에서 멈춥니다.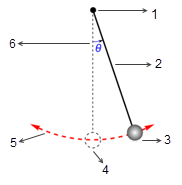
그림
1. 무마찰 피봇
2. 무질량 봉
3. 대용량 봅
4. 평형 위치
5. 봅 궤적
6. 진폭
또한 스윙 주기(기간)에서 진자가 가장 높은 위치 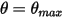 에 도달하면 운동 에너지의 총 손실에 따라 방향이 변경됩니다. 단순 중력 진자에서 운동 에너지는 잠재적 에너지로 완전히 전송되지만 매체의 저항을 고려할 때 점성 댐핑을 극복하기 위해 운동 에너지의 일부가 손실됩니다. 그러나 알짜 힘 또는 잠재적 에너지로 인해 진자가 평형 위치를 향해 반대 방향으로 이동하기 시작합니다. 여기서 운동 에너지(속도)는 최대이며 잠재적 에너지는 최저입니다. 이 경우
에 도달하면 운동 에너지의 총 손실에 따라 방향이 변경됩니다. 단순 중력 진자에서 운동 에너지는 잠재적 에너지로 완전히 전송되지만 매체의 저항을 고려할 때 점성 댐핑을 극복하기 위해 운동 에너지의 일부가 손실됩니다. 그러나 알짜 힘 또는 잠재적 에너지로 인해 진자가 평형 위치를 향해 반대 방향으로 이동하기 시작합니다. 여기서 운동 에너지(속도)는 최대이며 잠재적 에너지는 최저입니다. 이 경우 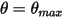 은 1-DOF 각 운동량 방정식 2.444에 대한 바운스 없음 조건을 나타냅니다.
은 1-DOF 각 운동량 방정식 2.444에 대한 바운스 없음 조건을 나타냅니다.
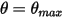 에 도달하면 운동 에너지의 총 손실에 따라 방향이 변경됩니다. 단순 중력 진자에서 운동 에너지는 잠재적 에너지로 완전히 전송되지만 매체의 저항을 고려할 때 점성 댐핑을 극복하기 위해 운동 에너지의 일부가 손실됩니다. 그러나 알짜 힘 또는 잠재적 에너지로 인해 진자가 평형 위치를 향해 반대 방향으로 이동하기 시작합니다. 여기서 운동 에너지(속도)는 최대이며 잠재적 에너지는 최저입니다. 이 경우
에 도달하면 운동 에너지의 총 손실에 따라 방향이 변경됩니다. 단순 중력 진자에서 운동 에너지는 잠재적 에너지로 완전히 전송되지만 매체의 저항을 고려할 때 점성 댐핑을 극복하기 위해 운동 에너지의 일부가 손실됩니다. 그러나 알짜 힘 또는 잠재적 에너지로 인해 진자가 평형 위치를 향해 반대 방향으로 이동하기 시작합니다. 여기서 운동 에너지(속도)는 최대이며 잠재적 에너지는 최저입니다. 이 경우 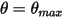 은 1-DOF 각 운동량 방정식 2.444에 대한 바운스 없음 조건을 나타냅니다.
은 1-DOF 각 운동량 방정식 2.444에 대한 바운스 없음 조건을 나타냅니다.바운스 없음 조건 외에도 제한 위치의 이동 바디는 운동 에너지를 전혀 손실하지 않고 뒤로 바운스하거나(완전 바운스) 해당 운동 에너지의 일부만 손실할 수 있습니다(부분 바운스). 따라서 흐름 도메인에 대한 벽 경계 또는 솔리드 바디의 동작을 결정하기 위해 변환 및 회전의 1-DOF 역학 방정식 방정식 2.432 및 방정식 2.444를 풀 때 다음 세 가지 바운스 조건이 적용됩니다.
• 바운스 없음 - Creo Flow Analysis의 기본 모델입니다. 이렇게 하면 솔리드 바디 또는 경계가 해당 동작의 한계에 도달할 때 해당 운동 에너지의 총 손실에 따라 방향이 변경됩니다. 바운스 및 입사를 나타내는 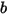 및
및  와
와 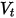 및
및 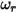 전환 및 회전 속도(속도 크기만 해당)를 사용하는 경우 이 바운스 모델은 다음과 같이 표현됩니다.
전환 및 회전 속도(속도 크기만 해당)를 사용하는 경우 이 바운스 모델은 다음과 같이 표현됩니다.
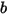 및
및  와
와 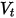 및
및 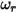 전환 및 회전 속도(속도 크기만 해당)를 사용하는 경우 이 바운스 모델은 다음과 같이 표현됩니다.
전환 및 회전 속도(속도 크기만 해당)를 사용하는 경우 이 바운스 모델은 다음과 같이 표현됩니다.◦ 변환
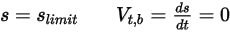
방정식 2.449
◦ 회전
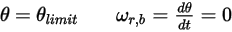
방정식 2.450
• 부분 바운스 - 솔리드 바디 또는 경계가 해당 동작의 한계에 도달할 때 사용자가 지정한 계수인 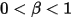 에 의해 결정되는 해당 운동 에너지의 부분 손실에 따라 방향이 변경되도록 지정하는 모델입니다.
에 의해 결정되는 해당 운동 에너지의 부분 손실에 따라 방향이 변경되도록 지정하는 모델입니다.
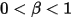 에 의해 결정되는 해당 운동 에너지의 부분 손실에 따라 방향이 변경되도록 지정하는 모델입니다.
에 의해 결정되는 해당 운동 에너지의 부분 손실에 따라 방향이 변경되도록 지정하는 모델입니다.◦ 변환
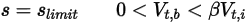
방정식 2.451
◦ 회전
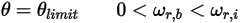
방정식 2.452
• 완전 바운스 - 솔리드 바디 또는 경계가 동작의 한계에 도달할 때 해당 운동 에너지 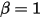 손실이 0인 상태에 따라 방향을 변경하도록 지정하는 모델입니다.
손실이 0인 상태에 따라 방향을 변경하도록 지정하는 모델입니다.
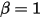 손실이 0인 상태에 따라 방향을 변경하도록 지정하는 모델입니다.
손실이 0인 상태에 따라 방향을 변경하도록 지정하는 모델입니다.◦ 변환

방정식 2.453
◦ 회전

방정식 2.454
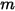 은 이동 객체의 질량입니다.
은 이동 객체의 질량입니다. 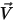 은 선형/변환 속도이고,
은 선형/변환 속도이고, 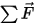 은 변환 대상 바디에 적용된 총/알짜 힘입니다.
은 변환 대상 바디에 적용된 총/알짜 힘입니다. 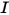 은 관성 모멘트입니다.
은 관성 모멘트입니다. 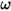 은 각속도이고,
은 각속도이고, 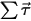 은 회전 바디에 적용된 총/알짜 토크입니다.
은 회전 바디에 적용된 총/알짜 토크입니다.