Modelli di cavitazione
In Creo Flow Analysis, così come nel modello Singhal et al originale, il fluido di lavoro nei flussi di cavitazione viene considerato sempre una miscela di liquido, vapore e alcuni gas non condensabili. Per default, i modelli di cavitazione considerano sia il cambiamento di fase liquido-vapore che l'effetto dei gas non condensabili. In base all'approccio di modellazione per effetto dei gas non condensabili, nella tabella di seguito vengono forniti cinque modello differenti per la previsione dell'aerazione e della cavitazione in un sistema liquido. Tali modelli vengono descritti in dettaglio in questa sezione.
|
Modelli per gas non condensabili
|
Descrizione
|
|---|---|
|
Frazione costante di massa di gas
|
La frazione di massa del gas non condensabile è costante ed è considerata fuori soluzione con bolle compressibili minuscole
|
|
Frazione variabile di massa di gas
|
Simile al modello della frazione costante di massa di gas, con la differenza che la frazione di massa del gas non condensabile può variare, ad esempio gli ingressi potrebbero determinare l'introduzione di frazioni di massa diverse
|
|
Modello a gas disciolto in equilibrio
|
La frazione di massa del gas non condensabile disciolto nel liquido è uguale al valore di equilibrio
|
|
Modello a gas disciolto
|
La frazione di massa del gas non condensabile disciolto nel liquido dipende dalla velocità di assorbimento o desorbimento e dal valore di equilibrio
|
|
Modello a gas completo
|
Combina il modello a gas disciolto e la frazione variabile di massa di gas
|
Modello della frazione costante di massa di gas
Il modello della frazione costante di massa di gas è il modello di cavitazione di base o di default in Creo Flow Analysis. È basato sul lavoro di Singhal et al. Questo modello presuppone che il fluido operativo, il gas non condensabile sempre presente (NCG) nel liquido, è un gas non solubile o senza bolle che segue la legge del gas ideale. Sebbene tutto il gas non condensabile predescritto possa espandersi liberamente con la diminuzione di pressione nelle zone di cavitazione, la frazione di massa di un gas non condensabile viene predescritta e rimane inalterata in un flusso di cavitazione:
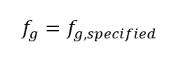
equazione 2.217
dove il fg,specificato è valore definito dall'utente.
La densità del gas non condensabile segue la legge del gas ideale:
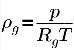
equazione 2.218
dove T è la temperatura del fluido, che può essere predescritta (flusso isotermico) o essere ottenuta risolvendo l'equazione 2.168 di conservazione dell'energia della miscela quando viene considerato il trasferimento di calore. Dall'equazione 2.173, la frazione di volume del gas non condensabile è la seguente:
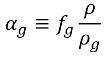
equazione 2.219
Chiaramente, sebbene la frazione di massa del gas non condensabile è fissa e in genere ha un valore piccolo, 1,5e-05 o 15 ppm nell'acqua naturale, la relativa frazione di volume αg varia e il suo valore può essere considerevolmente maggiore. Nelle cavità o nelle zone di bassa pressione il gas non condensabile riempie il vuoto nello spazio alternandosi al vapore in base alle densità del gas e del vapore.
Per il trasferimento di massa di liquido-vapore, l'equazione 2.194 e l'equazione 2.195 funzionano da base per costruire l'origine di cavitazione e il termine di risucchio nell'equazione 2.169 della frazione di massa di vapore. In particolare, il raggio della bolla, RB deve essere stimato utilizzando le quantità note di flusso durante lo sviluppo e la compressione delle bolle. Singhal et al ha affermato che se la tipica dimensione delle bolle RB è uguale alla loro dimensione limite (massima possibile), RB può essere determinata dall'equilibrio tra il trascinamento aerodinamico e le forze di tensione superficiali. Una correlazione utilizzata nell'industria nucleare è data da:
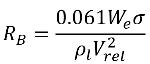
equazione 2.220
dove Vrel è la grandezza della velocità relativa di liquido-vapore. In un regime di flusso a bolle (in cui si verifica la cavitazione), Vrel è in genere inferiore del 5-10% circa rispetto alla velocità del liquido. Utilizzando diversi argomenti di limitazione come RB →0 e αv →0 e tenendo in considerazione che le velocità di cambiamento di fase per volume unitario devono essere proporzionali alle frazioni di volume (o alle frazioni di massa) della fase erogatrice, le espressioni per le velocità di creazione o condensazione di vapore sono ottenute per completare il modello di cavitazione come riportato di seguito.
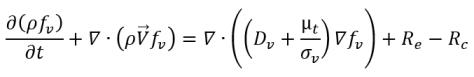
equazione 2.221
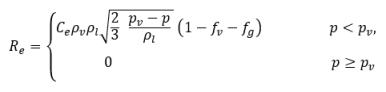
equazione 2.222
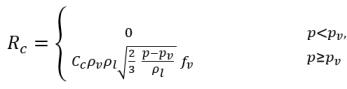
equazione 2.223
dove Ce e Cc sono i coefficienti di evaporazione e di condensazione, che possono essere valori costanti specificati dall'utente impostati di default su 1.0 o funzioni di quantità di flusso note. Nell'equazione 2.222 e nell'equazione 2.223, una nuova pressione di soglia ρv è introdotta per sostituire la pressione del vapore di saturazione ρsat nell'equazione 2.194 e nell'equazione 2.195. Secondo Singhal et al, per tenere conto dell'effetto della turbolenza sui flussi di cavitazione osservata attraverso analisi sperimentali, un valore locale delle fluttuazioni della pressione turbolenta fornito da Hinze:
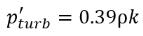
equazione 2.224
viene aggiunto alla pressione del vapore di saturazione per aumentare il valore della pressione soglia del cambiamento di fase in:
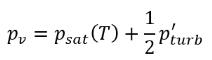
equazione 2.225
Per i flussi laminari, pv=psat(T)
Quando il trasferimento di calore viene tenuto in considerazione e tutte le densità di fase, inclusi liquido, vapore e gas condensabili sono soggetti a modifiche di temperatura, la pressione del vapore di saturazione psat è anch'essa funzione della temperatura. Di conseguenza, in questo modello di cavitazione, l'effetto termico diretto sulla cavitazione può essere preso in considerazione.
Modello della frazione variabile di massa di gas
Il modello della frazione variabile di massa di gas presuppone che il gas non condensabile rimanga sempre come gas libero che non può essere disciolto nel liquido, ma la frazione di massa non è più una costante predescritta come nel modello costante della frazione di massa di gas. Al contrario, la distribuzione della frazione di massa locale viene governata da un'equazione di trasporto. Il trasferimento di massa liquido-vapore è invece modellato dallo stesso modello di cavitazione referenziato nell'equazione 2.221, nell'equazione 2.222 e nell'equazione 2.223. Per maggior chiarezza, l'insieme completo delle equazioni di modellazione è fornito di seguito.
• Cambiamento di fase liquido-vapore
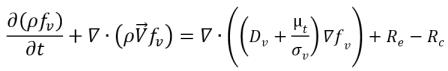
equazione 2.226
dove:
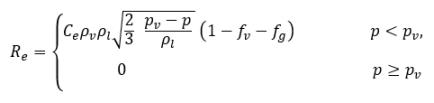
equazione 2.227
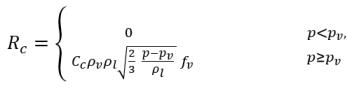
equazione 2.228
• Equazione di trasporto dei gas non condensabili
A seguito dell'equazione 2.199, l'equazione di trasporto per il gas non condensabile (fg) è data da:
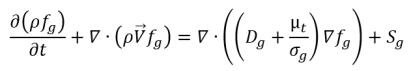
equazione 2.229
dove Sg corrisponde all'origine esterna o definita dall'utente per il gas non condensabile.
Modello a gas disciolto in equilibrio
Nei flussi di cavitazione, i gas non condensabili nel fluido vengono disciolti o emessi da un liquido per ottenere un equilibrio dinamico delle concentrazioni di massa tra le fasi liquida e gassosa. Nel modello a gas disciolto in equilibrio si presume che la frazione di massa del gas non condensabile totale resti costante. Tuttavia, una parte di essa viene disciolta nel liquido per soddisfare immediatamente la condizione di equilibrio locale. Dal punto di vista matematico, oltre alla stessa equazione della frazione di massa per il vapore e ai modelli di trasferimento di massa di vapore, risolve un'equazione di trasporto aggiuntiva per la frazione di massa del gas disciolto fgd, che si presuppone sia sempre in uno stato di equilibrio. Le equazioni di modellazione sono descritte di seguito.
• Cambiamento di fase liquido-vapore
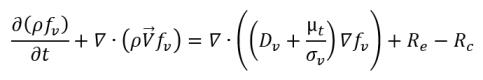
equazione 2.230
dove:
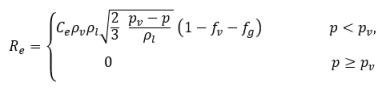
equazione 2.231
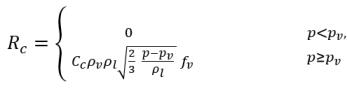
equazione 2.232
• Assorbimento/discioglimento o emissione di gas
Dall'equazione 2.197, l'equazione 2.211 e l'equazione 2.212, l'equazione di trasporto dei gas disciolti ha la seguente forma:
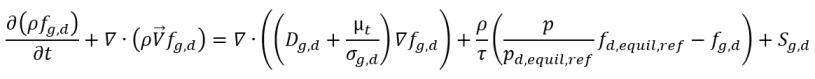
equazione 2.233
dove:
Sg,d | legge del discioglimento o dell'emissione dei gas definita dall'utente |
fd,equil,ref | frazione di massa in equilibrio del gas disciolto alla pressione di riferimento pd,equil,ref |
fd,equil,ref e pd,equil,ref | valori specificati dall'utente |
In questo modello di equilibrio, la scala temporale Γ si avvicina a zero in modo che il trasferimento di massa sia quasi istantaneo. Notate che nell'equazione 2.231, il gas libero ha la frazione di massa fg,f invece di fg. La frazione di massa del gas libero viene ottenuta dalla condizione:
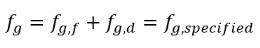
equazione 2.234
dove il fg,specificato è valore definito dall'utente.
Modello a gas disciolto
Questo modello rilassa la condizione che il gas disciolto nel liquido è sempre in uno stato di equilibrio. Anziché essere determinato dalla condizione di equilibrio con il trasferimento di massa istantaneo, la frazione di massa del gas disciolto (fg,d) dipende dal trasporto del componente e del tasso di discioglimento o di emissione (velocità finita). Di conseguenza, il modello a gas disciolto condivide le stesse formule di modellazione del modello a gas disciolto in equilibrio, equazione 2.230equazione 2.234. Tuttavia, le velocità finite del trasferimento di massa per il discioglimento e l'emissione di gas sono caratterizzate da scale temporali diverse (Γ). Per l'assorbimento o il discioglimento del gas nel liquido, Γ è dato da un tempo di assorbimento specificato (per default, il tempo di discioglimento del gas disciolto è 10 s). Per l'emissione del gas disciolto dal liquido, la velocità del trasferimento di massa è definita da un tempo di emissione del gas specificato (per default, il tempo di emissione del gas disciolto Γ è 10 s).
Modello a gas completo
Il modello a gas completo è una combinazione del modello a gas disciolto e del modello a gas variabile. La frazione di massa del gas non condensabile è soggetta a modifica con tempo e spazio, mentre il discioglimento del gas o l'assorbimento e l'emissione possono verificarsi anche per i gas non condensabili. La serie completa di equazioni di modellazione è riportata di seguito.
• Cambiamento di fase liquido-vapore
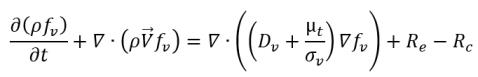
equazione 2.235
dove:
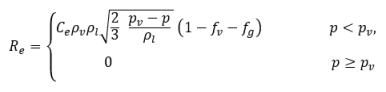
equazione 2.236
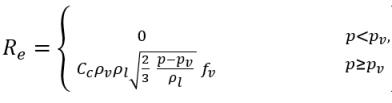
equazione 2.237
• Trasporto di gas non condensabile
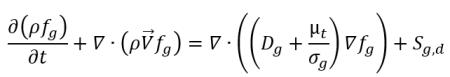
equazione 2.238
• Discioglimento o emissione di gas
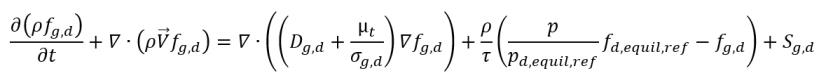
equazione 2.239