ODE Solver
The ordinary differential equations (ODE) equation 2.432 and equation 2.444 that govern the 1-DOF translation and rotation of the boundaries and volumes respectively, are solved numerically in Creo Flow Analysis. Specifically, to calculate a boundary and volume movement and displacement for remeshing, the following time-marching schemes are adopted to integrate the ODE equations: Stiff, Euler, and Runge-Kutta explicit solver.
Integration of One-DOF Translation Equation
Substituting equation 2.434, equation 2.435, equation 2.436 into equation 2.432 and grouping the explicit force terms into a single term, 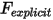 for brevity, you rewrite the 1-DOF translation equation of motion in the following form:
for brevity, you rewrite the 1-DOF translation equation of motion in the following form:
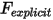 for brevity, you rewrite the 1-DOF translation equation of motion in the following form:
for brevity, you rewrite the 1-DOF translation equation of motion in the following form: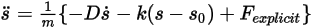
Equation 2.455
where the explicitly calculated force term 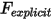 is:
is:
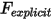 is:
is:
Equation 2.456
With given initial and boundary conditions, the displacement of the solid body is obtained by integrating equation 2.455 using explicit time-marching schemes. Over time-step 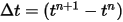 , you have the general formulations as follows:
, you have the general formulations as follows:
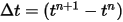 , you have the general formulations as follows:
, you have the general formulations as follows: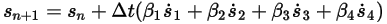
Equation 2.457
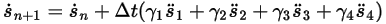
Equation 2.458
where the weighting factors sum to unity:
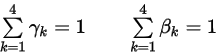
Equation 2.459
With the choice of weighting factors, different schemes are derived. For example, the Euler and Runge-Kutta explicit schemes follow:
• Euler Explicit Solver (1st–Order)
With 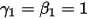 and
and 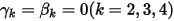 , you have the Euler explicit scheme in the following:
, you have the Euler explicit scheme in the following:
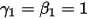 and
and 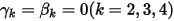 , you have the Euler explicit scheme in the following:
, you have the Euler explicit scheme in the following: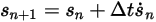
Equation 2.460
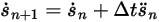
Equation 2.461
• Runge-Kutta Explicit Solver
The Runge-Kutta solvers are 2nd-order and 4th-order explicit schemes, which follow:
◦ Second-Order Scheme
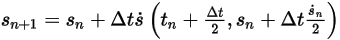
Equation 2.462
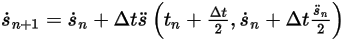
Equation 2.463
◦ Fourth-Order Scheme
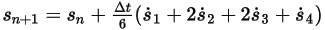
Equation 2.464
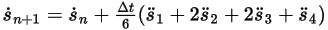
Equation 2.465
where,

Equation 2.466

Equation 2.467

Equation 2.468

Equation 2.469
• Stiff Solver (Explicit)
In addition to the standard Euler and Runge-Kutta schemes, Creo Flow Analysis has developed its stiff solver to integrate the translation 1-DOF ODE equation. It is the default method for dynamic motions of solid bodies.
Integration of One-DOF Rotation Equation
As for the translation, substituting equation 2.446 and equation 2.447 into equation 2.444 and grouping the explicit torque terms into a single term  for brevity, you rewrite the 1-DOF rotation equation of motion, equation 2.444 in the following form:
for brevity, you rewrite the 1-DOF rotation equation of motion, equation 2.444 in the following form:
 for brevity, you rewrite the 1-DOF rotation equation of motion, equation 2.444 in the following form:
for brevity, you rewrite the 1-DOF rotation equation of motion, equation 2.444 in the following form: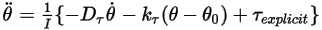
Equation 2.470
where the explicitly calculated torque term 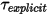 is:
is:
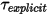 is:
is:
Equation 2.471
With given initial and boundary conditions, the angle of rotation is obtained by integrating equation 2.470 using explicit time-marching schemes. Over time-step 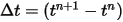 , you have the general formulations as follows:
, you have the general formulations as follows:
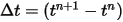 , you have the general formulations as follows:
, you have the general formulations as follows: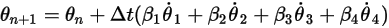
Equation 2.472
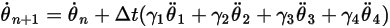
Equation 2.473
where the weighting factors sum to unity:
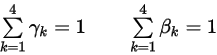
Equation 2.474
With the choice of weighting factors, different numerical schemes are easily derived. Again, the Euler and Runge-Kutta explicit schemes are given below:
• Euler Explicit Solver (1st–Order)
With 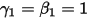 and
and 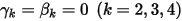 , you have the Euler explicit scheme in the following:
, you have the Euler explicit scheme in the following:
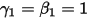 and
and 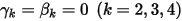 , you have the Euler explicit scheme in the following:
, you have the Euler explicit scheme in the following: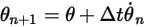
Equation 2.475
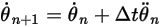
Equation 2.476
• Runge-Kutta Explicit Solver
The Runge-Kutta solvers are 2nd-order and 4th-order explicit schemes that are given below:
◦ Second-Order Scheme
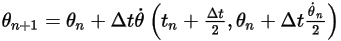
Equation 2.477
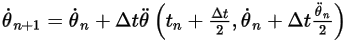
Equation 2.478
◦ Fourth-Order Scheme
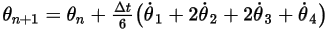
Equation 2.479
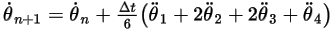
Equation 2.480
where,

Equation 2.481

Equation 2.482

Equation 2.483

Equation 2.484
• Stiff Solver (Explicit)
In addition to the standard Euler and Runge-Kutta schemes, Creo Flow Analysis has developed its stiff solver to integrate the 1-DOF rotation ODE equation 2.444. It is the default method for dynamics motions of solid bodies.