Motions of a Rigid Body
In simulations, the surfaces of a solid object are usually wall boundaries in a flow domain. When a solid object or surface is subjected to dynamic and mechanical forces, and thermal effect, the imbalance of the net forces can cause the body to move and deform. A solid object is often considered as a rigid body in flow simulations. Therefore, for a solid object subjected to force imbalances, you assume that it can move linearly (translation), angularly (rotation), or both linearly and angularly, without deformation. For a CFA computational domain, however, the boundary movement can lead to the domain change and consequently, the volume mesh may deform, as described in the Flow module.
For a rigid body, the equations governing its motions are derived directly from the conservation of linear and angular momentum:
• Linear Momentum (Translation)
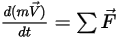
Equation 2.426
• Angular Momentum (Rotation)
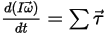
Equation 2.427
In equation 2.426, 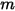 is the mass of the moving object;
is the mass of the moving object; 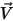 ⃗ is the linear/transitional velocity; and
⃗ is the linear/transitional velocity; and 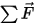 ⃗ is the total/net forces exerted on the body under translation. In equation 2.427,
⃗ is the total/net forces exerted on the body under translation. In equation 2.427, 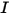 is the moment of inertia;
is the moment of inertia; 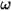 ⃗ is the angular velocity; and
⃗ is the angular velocity; and 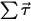 ⃗ is the total/net torque acted on the rotating body.
⃗ is the total/net torque acted on the rotating body.
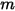 is the mass of the moving object;
is the mass of the moving object; 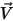 ⃗ is the linear/transitional velocity; and
⃗ is the linear/transitional velocity; and 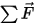 ⃗ is the total/net forces exerted on the body under translation. In equation 2.427,
⃗ is the total/net forces exerted on the body under translation. In equation 2.427, 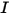 is the moment of inertia;
is the moment of inertia; 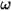 ⃗ is the angular velocity; and
⃗ is the angular velocity; and 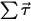 ⃗ is the total/net torque acted on the rotating body.
⃗ is the total/net torque acted on the rotating body.Equation 2.426 and equation 2.427 govern the general motions of a solid body, which have six degrees of freedom (6-DOF) with three degrees each for translation (3-DOF) and rotation (3-DOF), respectively. Creo Flow Analysis considers only 1-DOF translation and rotation, which are explained in this section.
One-DOF Translation
With the assumption that a solid body moves linearly in an arbitrarily specified direction (remain unchanged), defined by a unit vector 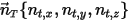 , the translational motion of the body is reduced to be one degree of freedom (1-DOF). As a result, for the linear momentum conservation, equation 2.426 becomes a scalar equation along the moving direction since the moving velocity and force are expressed in terms of
, the translational motion of the body is reduced to be one degree of freedom (1-DOF). As a result, for the linear momentum conservation, equation 2.426 becomes a scalar equation along the moving direction since the moving velocity and force are expressed in terms of 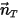 :
:
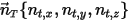 , the translational motion of the body is reduced to be one degree of freedom (1-DOF). As a result, for the linear momentum conservation, equation 2.426 becomes a scalar equation along the moving direction since the moving velocity and force are expressed in terms of
, the translational motion of the body is reduced to be one degree of freedom (1-DOF). As a result, for the linear momentum conservation, equation 2.426 becomes a scalar equation along the moving direction since the moving velocity and force are expressed in terms of 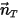 :
: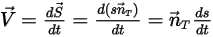
Equation 2.428
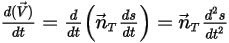
Equation 2.429
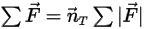
Equation 2.430
where 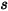 is the magnitude of the position vector
is the magnitude of the position vector 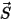 at a point of interest on the solid body along the moving direction
at a point of interest on the solid body along the moving direction 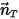 . In a Cartesian coordinate system, you have
. In a Cartesian coordinate system, you have
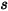 is the magnitude of the position vector
is the magnitude of the position vector 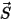 at a point of interest on the solid body along the moving direction
at a point of interest on the solid body along the moving direction 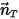 . In a Cartesian coordinate system, you have
. In a Cartesian coordinate system, you have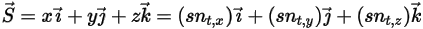
Equation 2.431
If mass of the solid body remains a constant, and you expand the force term to explicitly include all the forces applied on the body, you have the scalar linear momentum equation as:
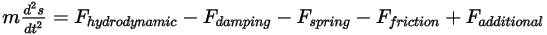
Equation 2.432
The forces on the right side indicate the following:
• Hydrodynamic Force  —Consists of pressure and shear forces. They are caused by the relative motion between the fluid flow and the surfaces of the solid body which are in contact with the flow. The pressure and shear forces are obtained from the flow solutions (output quantities):
—Consists of pressure and shear forces. They are caused by the relative motion between the fluid flow and the surfaces of the solid body which are in contact with the flow. The pressure and shear forces are obtained from the flow solutions (output quantities):
 —Consists of pressure and shear forces. They are caused by the relative motion between the fluid flow and the surfaces of the solid body which are in contact with the flow. The pressure and shear forces are obtained from the flow solutions (output quantities):
—Consists of pressure and shear forces. They are caused by the relative motion between the fluid flow and the surfaces of the solid body which are in contact with the flow. The pressure and shear forces are obtained from the flow solutions (output quantities):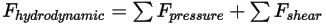
Equation 2.433
• Damping force 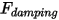 —A retarding force caused by the frictional damping effect. It is determined by the motion of the solid object and the user-defined damping coefficient
—A retarding force caused by the frictional damping effect. It is determined by the motion of the solid object and the user-defined damping coefficient  :
:
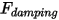 —A retarding force caused by the frictional damping effect. It is determined by the motion of the solid object and the user-defined damping coefficient
—A retarding force caused by the frictional damping effect. It is determined by the motion of the solid object and the user-defined damping coefficient  :
: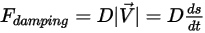
Equation 2.434
• Spring Force 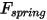 —Depends on the displacement of the string
—Depends on the displacement of the string 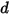 , spring constant
, spring constant 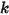 , and the spring preload force
, and the spring preload force 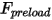 :
:
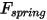 —Depends on the displacement of the string
—Depends on the displacement of the string 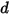 , spring constant
, spring constant 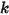 , and the spring preload force
, and the spring preload force 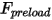 :
: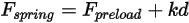
Equation 2.435
where the spring displacement 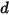 is defined as:
is defined as:
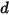 is defined as:
is defined as: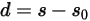
Equation 2.436
where 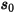 is the magnitude of the position vector
is the magnitude of the position vector 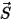 at previous location
at previous location 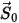 .
.
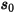 is the magnitude of the position vector
is the magnitude of the position vector 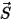 at previous location
at previous location 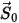 .
.• Friction Force—Contact friction model is adopted to account for the effect of friction in a dynamic system. The friction force 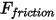 is modeled as:
is modeled as:
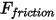 is modeled as:
is modeled as: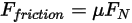
Equation 2.437
where  is the normal component of the contact force exerted on the solid surface of interest. For friction coefficient
is the normal component of the contact force exerted on the solid surface of interest. For friction coefficient 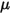 , the static friction coefficient
, the static friction coefficient 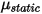 , and the sliding friction coefficient
, and the sliding friction coefficient 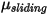 , are further introduced for the stationary and moving bodies, respectively:
, are further introduced for the stationary and moving bodies, respectively:
 is the normal component of the contact force exerted on the solid surface of interest. For friction coefficient
is the normal component of the contact force exerted on the solid surface of interest. For friction coefficient 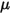 , the static friction coefficient
, the static friction coefficient 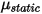 , and the sliding friction coefficient
, and the sliding friction coefficient 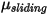 , are further introduced for the stationary and moving bodies, respectively:
, are further introduced for the stationary and moving bodies, respectively: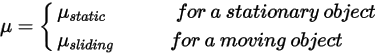
Equation 2.438
• Additional Force 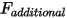 —Added for additional user-specified forces.
—Added for additional user-specified forces.
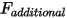 —Added for additional user-specified forces.
—Added for additional user-specified forces.One-DOF Rotation
When an arbitrary rotating axis is defined by a point (center of the axis) 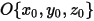 , and the directional unit vector
, and the directional unit vector 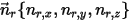 , the solid body rotation around the axis
, the solid body rotation around the axis 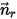 is also reduced to 1-DOF rotation. Similarly, for the angular momentum conservation, equation 2.427 also becomes a scalar equation along the tangential direction
is also reduced to 1-DOF rotation. Similarly, for the angular momentum conservation, equation 2.427 also becomes a scalar equation along the tangential direction 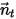 , defined as:
, defined as:
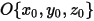 , and the directional unit vector
, and the directional unit vector 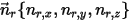 , the solid body rotation around the axis
, the solid body rotation around the axis 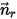 is also reduced to 1-DOF rotation. Similarly, for the angular momentum conservation, equation 2.427 also becomes a scalar equation along the tangential direction
is also reduced to 1-DOF rotation. Similarly, for the angular momentum conservation, equation 2.427 also becomes a scalar equation along the tangential direction 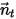 , defined as:
, defined as: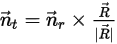
Equation 2.439
where 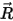 is the vector pointing from the center of the axis to an arbitrary point
is the vector pointing from the center of the axis to an arbitrary point 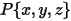 on the solid body:
on the solid body:
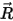 is the vector pointing from the center of the axis to an arbitrary point
is the vector pointing from the center of the axis to an arbitrary point 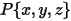 on the solid body:
on the solid body: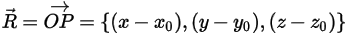
Equation 2.440
The angular velocity and torque at the point  are rephrased as:
are rephrased as:
 are rephrased as:
are rephrased as: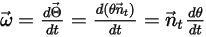
Equation 2.441
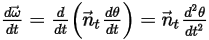
Equation 2.442
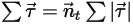
Equation 2.443
where, 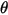 is the angle of rotation of the point
is the angle of rotation of the point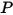 relative to the starting or reference location.
relative to the starting or reference location.
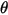 is the angle of rotation of the point
is the angle of rotation of the point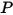 relative to the starting or reference location.
relative to the starting or reference location.If the moment of inertia remains a constant, and expanding the torque term to explicitly include all the torques applied on the rotating body, you have the scalar angular momentum equation as:
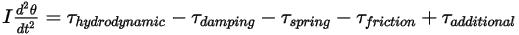
Equation 2.444
The torque terms on the right side are defined as follows:
• Hydrodynamic Torque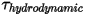 —Combination of torque due to pressure and shear forces:
—Combination of torque due to pressure and shear forces:
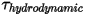 —Combination of torque due to pressure and shear forces:
—Combination of torque due to pressure and shear forces: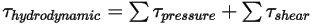
Equation 2.445
• Damping Torque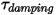 —Depends on the rotational speed
—Depends on the rotational speed 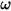 and the user-defined damping coefficient,
and the user-defined damping coefficient,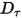 :
:
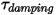 —Depends on the rotational speed
—Depends on the rotational speed 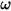 and the user-defined damping coefficient,
and the user-defined damping coefficient,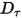 :
: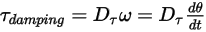
Equation 2.446
• Spring Torque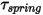 —Torque induced by torsion that depends on the displacement angle
—Torque induced by torsion that depends on the displacement angle 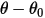 , the user-defined preload torque
, the user-defined preload torque 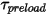 , and the torsion constant
, and the torsion constant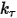 .
.
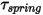 —Torque induced by torsion that depends on the displacement angle
—Torque induced by torsion that depends on the displacement angle 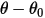 , the user-defined preload torque
, the user-defined preload torque 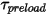 , and the torsion constant
, and the torsion constant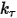 .
.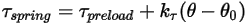
Equation 2.447
where 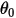 is the reference angle. It is typically the position of the boundary or volume during the model set-up but can correspond to a different location. For example, at zero angular displacement, the reference angle
is the reference angle. It is typically the position of the boundary or volume during the model set-up but can correspond to a different location. For example, at zero angular displacement, the reference angle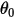 is not the same as the initial angular position.
is not the same as the initial angular position.
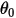 is the reference angle. It is typically the position of the boundary or volume during the model set-up but can correspond to a different location. For example, at zero angular displacement, the reference angle
is the reference angle. It is typically the position of the boundary or volume during the model set-up but can correspond to a different location. For example, at zero angular displacement, the reference angle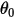 is not the same as the initial angular position.
is not the same as the initial angular position.• Friction Torque—Torque caused by the frictional force that occurs when two objects in contact move. In experiments, it is determined by the difference between the applied torque and observed or net torque. It depends on the friction coefficient 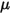 and the contact torque due to the normal force
and the contact torque due to the normal force 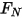 applied on the contact surface:
applied on the contact surface:
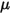 and the contact torque due to the normal force
and the contact torque due to the normal force 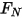 applied on the contact surface:
applied on the contact surface: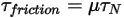
Equation 2.448
where 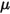 is a user-defined parameter, defined in equation 2.438.
is a user-defined parameter, defined in equation 2.438.
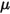 is a user-defined parameter, defined in equation 2.438.
is a user-defined parameter, defined in equation 2.438.• Additional Torques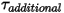 —Added for additional user-specified torques.
—Added for additional user-specified torques.
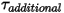 —Added for additional user-specified torques.
—Added for additional user-specified torques.Bounce Model
In many situations, a solid body only translate, rotates, or both translates and rotates, in a limited space (limited distance or angle), namely, it has a maximum, minimum, or both a maximum and a minimum position. For example, as shown in the following figure, when a simple gravity pendulum is released from the original position with the angle 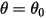 , the restoring force acting on the its mass causes it to oscillate about the equilibrium position. The maximum angle on either side of the equilibrium position
, the restoring force acting on the its mass causes it to oscillate about the equilibrium position. The maximum angle on either side of the equilibrium position 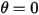 depends on its releasing position
depends on its releasing position 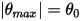 . If there is no friction (frictionless pivot and in vacuum), the maximum angle remains unchanged and the pendulum swings back and forth permanently with the same extreme positions. However, when a pendulum is in the atmosphere, for example, the air resistance (damping) causes the maximum swinging angle to reduce with time and eventually stop at the equilibrium position.
. If there is no friction (frictionless pivot and in vacuum), the maximum angle remains unchanged and the pendulum swings back and forth permanently with the same extreme positions. However, when a pendulum is in the atmosphere, for example, the air resistance (damping) causes the maximum swinging angle to reduce with time and eventually stop at the equilibrium position.
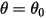 , the restoring force acting on the its mass causes it to oscillate about the equilibrium position. The maximum angle on either side of the equilibrium position
, the restoring force acting on the its mass causes it to oscillate about the equilibrium position. The maximum angle on either side of the equilibrium position 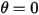 depends on its releasing position
depends on its releasing position 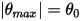 . If there is no friction (frictionless pivot and in vacuum), the maximum angle remains unchanged and the pendulum swings back and forth permanently with the same extreme positions. However, when a pendulum is in the atmosphere, for example, the air resistance (damping) causes the maximum swinging angle to reduce with time and eventually stop at the equilibrium position.
. If there is no friction (frictionless pivot and in vacuum), the maximum angle remains unchanged and the pendulum swings back and forth permanently with the same extreme positions. However, when a pendulum is in the atmosphere, for example, the air resistance (damping) causes the maximum swinging angle to reduce with time and eventually stop at the equilibrium position.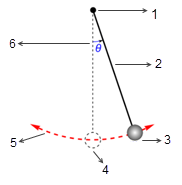
figure
1. Frictionless Pivot
2. Massless Rod
3. Massive Bob
4. Equilibrium Position
5. Bob’s Trajectory
6. Amplitude
Furthermore, in a swinging cycle (period), when the pendulum reaches the highest position 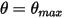 , it changes direction with the total loss of its kinetic energy. In the simple gravity pendulum, the kinetic energy is completely transferred into potential energy, while when you consider resistance of the medium, a part of the kinetic energy is lost to overcome the viscous damping. However, the net force or the potential energy drives the pendulum to start moving in the opposition direction towards the equilibrium position, where the kinetic energy (speed) is the maximum while the potential is the lowest. In this case,
, it changes direction with the total loss of its kinetic energy. In the simple gravity pendulum, the kinetic energy is completely transferred into potential energy, while when you consider resistance of the medium, a part of the kinetic energy is lost to overcome the viscous damping. However, the net force or the potential energy drives the pendulum to start moving in the opposition direction towards the equilibrium position, where the kinetic energy (speed) is the maximum while the potential is the lowest. In this case,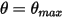 indicates a no bounce condition for the 1-DOF angular momentum equation 2.444.
indicates a no bounce condition for the 1-DOF angular momentum equation 2.444.
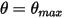 , it changes direction with the total loss of its kinetic energy. In the simple gravity pendulum, the kinetic energy is completely transferred into potential energy, while when you consider resistance of the medium, a part of the kinetic energy is lost to overcome the viscous damping. However, the net force or the potential energy drives the pendulum to start moving in the opposition direction towards the equilibrium position, where the kinetic energy (speed) is the maximum while the potential is the lowest. In this case,
, it changes direction with the total loss of its kinetic energy. In the simple gravity pendulum, the kinetic energy is completely transferred into potential energy, while when you consider resistance of the medium, a part of the kinetic energy is lost to overcome the viscous damping. However, the net force or the potential energy drives the pendulum to start moving in the opposition direction towards the equilibrium position, where the kinetic energy (speed) is the maximum while the potential is the lowest. In this case,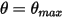 indicates a no bounce condition for the 1-DOF angular momentum equation 2.444.
indicates a no bounce condition for the 1-DOF angular momentum equation 2.444.In addition to the no-bounce condition, a moving body at the limiting position may not lose any kinetic energy at all and bounce back (perfect bounce), or only lose a part of its kinetic energy (partial bounce). Therefore, the following three bounce conditions are applied when the 1-DOF dynamics equations of translation and rotation, equation 2.432, and equation 2.444, are solved to determine the motions of a solid body or a wall boundary for the flow domain:
• No Bounce—Default model in Creo Flow Analysis. This determines that when a solid body or boundary reaches the limit of its motion, it changes direction with the total loss of its kinetic energy. With 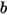 and
and  representing bounce and incidence, and
representing bounce and incidence, and 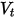 and
and 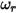 translational and rotating speed (magnitude only), this bounce model is expressed as follows:
translational and rotating speed (magnitude only), this bounce model is expressed as follows:
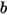 and
and  representing bounce and incidence, and
representing bounce and incidence, and 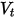 and
and 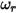 translational and rotating speed (magnitude only), this bounce model is expressed as follows:
translational and rotating speed (magnitude only), this bounce model is expressed as follows:◦ Translation
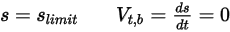
Equation 2.449
◦ Rotation
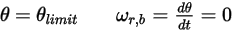
Equation 2.450
• Partial Bounce—Model that dictates that when a solid body or boundary reaches the limit of its motion, it changes direction with the partial loss of its kinetic energy, determined by a user-specified factor,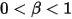 :
:
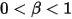 :
:◦ Translation
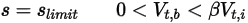
Equation 2.451
◦ Rotation
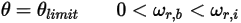
Equation 2.452
• Perfect Bounce—Model that dictates that when a solid body or boundary reaches the limit of its motion, it changes direction with zero loss of its kinetic energy, 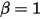 :
:
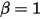 :
:◦ Translation

Equation 2.453
◦ Rotation

Equation 2.454