Теория моделей кавитации
В уравнении 2.169 переноса пара Re и Rc - это характеристики источника переноса массы, связанные с ростом и схлопыванием пузырьков пара в кавитационных потоках. Эти условия и переменные учитываются для расчета обмена масс между паровой и жидкой фазами во время процесса кавитации. Re и Rc моделируются в уравнении Рэлея - Плессета (Rayleigh-Plesset), описывающем рост одного пузырька пара в жидкости.
Перенос массы "жидкость-пар"
Чтобы получить выражение для результирующей скорости фазового перехода в кавитации, рассматривайте несжимаемый жидкий пар как два фазовых потока с нулевой скоростью скольжения, где неконденсирующийся газ не рассматривается. Если ввести R для представления результирующей скорости переноса массы из жидкости в пар, то уравнения объемных долей жидкости и пара и уравнение непрерывности полной массы можно представить следующим образом:
• Жидкая фаза
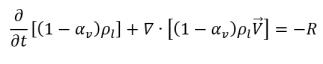
уравнение 2.179
• Фаза пара
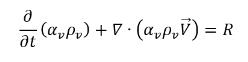
уравнение 2.180
• Смесь (непрерывность общей массы)
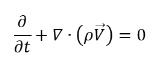
уравнение 2.181
В двухфазной системе "жидкость-пар" плотность смеси ρ выражается через объемную долю пара и плотности фаз:
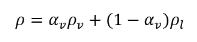
уравнение 2.182
Поскольку предполагается, что обе плотности - жидкости и пара - постоянны (несжимаемы), отношение между градиентом скорости и долей объема пара выводится из уравнения 2.181 и уравнения 2.182:
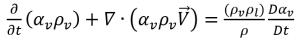
уравнение 2.183
Комбинация уравнений 2.179 и уравнение 2.183 дает следующее выражение для характеристики источника общей массы:
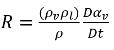
уравнение 2.184
Если подставить уравнение 2.184 в уравнение 2.180, уравнение для объемной доли пара можно переписать в общем виде:
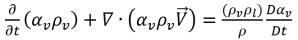
уравнение 2.185
Если применить соотношение между массовой долей и долей объема из уравнения 2.173 для пара, получится уравнение 2.185 в терминах массовой доли пара:
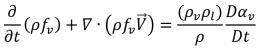
уравнение 2.186
Из уравнения 2.185 и уравнения 2.186 ясно, что при условии нулевой скорости скольжения между фазами жидкости и пара кавитацию можно моделировать как однофазный поток с дополнительным транспортным уравнением для массовой доли пара или как эйлеровский поток многофазной смеси с переносом массы между фазами жидкости и пара. Если не учитывать эффект диффузии и различия в фазовой скорости, эти два подхода математически идентичны. Creo Flow Analysis использует однофазный метод для моделирования кавитационных потоков.
Описание динамики пузырьков
Для большинства природных ситуаций и технических систем в жидкости для возникновения кавитации должно существовать соответствующее число ядер, таких как пузырьки, неконденсируемые газы и т. д. Соответственно для моделирования процесса кавитации необходим, прежде всего, правильный расчет роста и схлопывания пузырьков. Если предположить, что в жидкости, движущейся в потоке, существует нулевая скорость скольжения между пузырьками жидкости и пара, уравнение динамики пузырьков выводится из обобщенного уравнения Релея - Плессета, описывающего рост газового пузырька в жидкости:
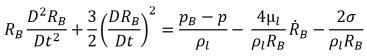
уравнение 2.187
где
RB | радиус пузырька |
pB | давление в пузырьке (предполагается, что это давление пара при данной температуре жидкости в отсутствие других газов) |
p | давление в жидкости, окружающей пузырек |
σ | коэффициент поверхностного натяжения между жидкостью и паром |
Это уравнение получается из механического баланса (нет тепловых барьеров для роста пузырьков).
Если пренебречь производной по времени второго порядка (для низкочастотных колебаний), членом вязкого трения и силой поверхностного натяжения, мы получим упрощенную форму уравнения 2.187, которая действительна для асимптотического состояния:
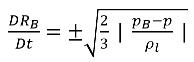
уравнение 2.188
Это упрощенное уравнение Релея - Плессета описывает физический подход, позволяющий ввести эффекты динамики пузырьков в модели кавитации. Радиус пузырьков может увеличиваться или уменьшаться в зависимости от знака выражений (pB - p): пузырек растет, если p < pB, и сжимается, если p > pB. Поэтому уравнение 2.188 переписывается следующим образом:
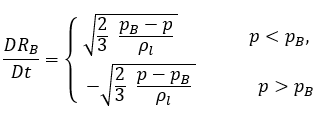
уравнение 2.189
Если η - это плотность числа пузырьков в жидкости (число пузырьков на единицу объема) и все пузырьки пара являются совершенными сферами с одинаковым радиусом RB, то объемная доля фазы пара имеет вид:
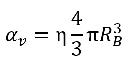
уравнение 2.190
Предполагается, что пузырьки пара не могут создаваться или разрушаться в жидкости, но они могут расти (испарение) и схлопываться (конденсация) во время процесса кавитации. В уравнении 2.190 плотность числа пузырьков пара (η) остается постоянной, но радиус пузырьков (RB) увеличивается или уменьшается. Тогда производная по времени доли объема пара может рассчитываться следующим образом:
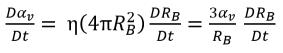
уравнение 2.191
Подстановка уравнения 2.191 в уравнение 2.186 дает транспортное уравнение, управляющее массовой долей паровой фазы:
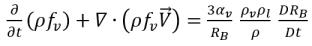
уравнение 2.192
Применение уравнения 2.189 дает для результирующей скорости переноса массы на единицу объема между жидкостью и паром следующий вид:
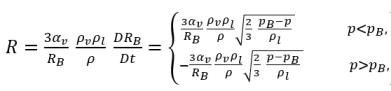
уравнение 2.193
где уравнение 2.193 показывает, что в кавитации скорость переноса массы в единице объема (R) является функцией (пропорциональна) плотности паровой и жидкой фаз, а также обратно пропорциональна плотности смеси. Поскольку уравнение 2.192 получено непосредственно из непрерывности фазы и массы смеси, оно является точным и должно точно представлять перенос массы между фазами жидкости и пара в кавитации. С введением динамики пузырьков уравнение 2.193 использует аналогичный метод для моделирования двух противоположных (и физически различающихся) процессов переноса массы: из жидкости в пар (рост или испарение пузырьков) и из пара в жидкость (схлопывание или конденсация пузырьков). Для транспортного уравнения 2.192 массовой доли пара рост пузырьков является характеристикой источника, в то время как схлопывание пузырьков обрабатывается как характеристика теплопоглощения.
В практических моделях кавитации локальное давление далекого поля p обычно считается совпадающим с давлением в центре ячейки. Давление пузырьков pB равно давлению насыщенного пара (psat, свойство материала) в отсутствие растворенных газов, движения масс и вязкого трения, pB = psat
Сравнивая уравнение 2.192 и уравнение 2.193 с общим уравнением 2.169 массовой доли пара, получаем следующие характеристики источника Re и Rc:
• Если локальное давление потока ниже давления насыщенного пара p<psat, возникает только испарение, так что:
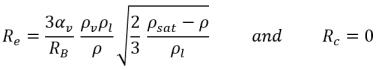
уравнение 2.194
• Если локальное давление потока выше давления насыщенного пара p>psat, существует только конденсация:
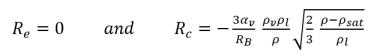
уравнение 2.195
Уравнение 2.194 и уравнение 2.195 формируют основу почти всех доступных механических двухфазных моделей кавитации. В Creo Flow Analysis использован метод моделирования Сингхала и др..
Поглощение/растворение и выделение газа
Неконденсирующиеся газы часто присутствуют в рабочей жидкости и могут оказывать значительное влияние на кавитацию. Иногда неконденсирующийся газ свободно перемещается с потоком, а также растворяется в жидкости или выделяется из жидкости, естественным образом стремящейся к динамическому равновесию концентраций масс между фазами жидкости и газа. Поглощение или растворение газа и выделение его в жидкости - это также явления переноса массы жидкости-газа, управляемое перепадами и градиентами концентраций массы. Чтобы моделировать кавитационные потоки, необходимо также учитывать воздействие неконденсирующегося газа и возможный перенос массы между жидкостью и газом в потоке смеси.
Если предположить, что в двухфазовом потоке "жидкость-газ" неконденсируемый газ, такой как воздух или кислород, существует и в фазе жидкости (растворенный газ), и в фазе газа (свободный газ), транспортные уравнения для массовой доли газа в каждой фазе будут следующими:
• Свободный газ (фаза газа)
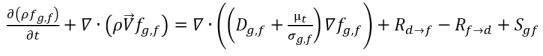
уравнение 2.196
• Растворенный газ (фаза жидкости)
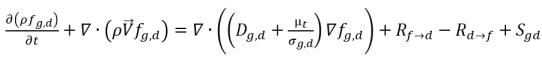
уравнение 2.197
где
fg,f | массовые доли свободного газа |
fg,d | массовые доли свободного газа и растворенного газа, |
Sg,f, Sg,d | внешние или определяемые пользователем источники. |
Dg,f | диффузионная способность свободного газа и растворенного газа |
Dg,d | диффузионная способность растворенного газа |
Если массовая доля неконденсирующегося газа предварительно описана как fg, получаем:
fg=fg,f
или его перемещение в пространстве и времени получается из решения следующего уравнения:
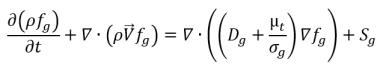
уравнение 2.199
Заметьте, что из числа трех уравнений - уравнение 2.196, уравнение 2.197 и уравнение 2.199 - только два должны решаться непосредственно.
В уравнении 2.196 и уравнении 2.197 источник Rd→f указывает уровень выделения растворенного газа, а Rf→d указывает уровень поглощения или растворения свободного газа.
Если эти две фазы соприкасаются, наблюдается тенденция к перемещению свободного газа f и растворенного газа d из одной фазы в другую, чтобы достигнуть динамического равновесия между этими двумя фазами. Модели равновесия предполагают, что волюметрические скорости переносов массы зависят от градиентов или различий в концентрациях масс:
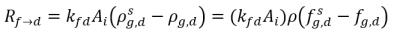
уравнение 2.200
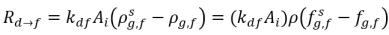
уравнение 2.201
где
AI | область на границе раздела жидкости-газа |
kf,d(=kd,f) | объемный коэффициент волюметрического переноса массы |
ρg,d(=ρfg,d) | локальные концентрации массы растворенного газа |
ρg,f(=ρfg,f) | локальные концентрации массы свободного газа |
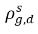 | равновесные концентрации массы растворенного газа в содержащих его фазах |
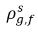 | равновесные концентрации массы свободного газа в содержащих его фазах |
Отметим, что в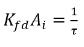 
используется единица измерения 1/с как показатель эффективности переноса массы. Таким образом, уравнение 2.200 и уравнение 2.201 также имеют следующий вид:
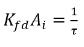используется единица измерения 1/с как показатель эффективности переноса массы. Таким образом, уравнение 2.200 и уравнение 2.201 также имеют следующий вид: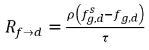
уравнение 2.202
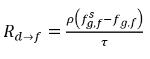
уравнение 2.203
Обычно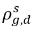 
и 
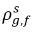не совпадают (нарушение непрерывности). Между этими двумя концентрациями существует четко определенная кривая равновесия, которая зависит от температуры, давления и состава смеси. Эта кривая, как правило, является монотонной и нелинейной и часто выражается как квазилинейное уравнение с коэффициентом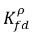 
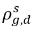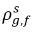и не совпадают (нарушение непрерывности). Между этими двумя концентрациями существует четко определенная кривая равновесия, которая зависит от температуры, давления и состава смеси. Эта кривая, как правило, является монотонной и нелинейной и часто выражается как квазилинейное уравнение с коэффициентом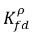 
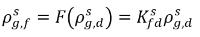
уравнение 2.204
где Kf,d обычно решается с помощью физических законов или эмпирических корреляций. Один общий метод заключается в выполнении закона Генри, обеспечивающего обобщенную равновесную взаимосвязь. Он утверждает, что для жидкой смеси, соприкасающейся с газовой фазой, частичное давление свободного газа ρg,f равно произведению равновесной мольной доли растворенного газа в жидкой фазе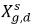 
и константы Генри, Hx:
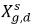и константы Генри, Hx: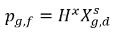
уравнение 2.205
Если для фазы свободного газа выполняется закон идеального газа, то закон Дальтона для частичного давления дает следующее уравнение:
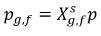
уравнение 2.206
Использование уравнения 2.204 - уравнения 2.206 создает следующее отношение равновесия:
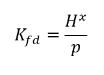
уравнение 2.207
Таким образом, константа Генри имеет единицу измерения давления и может рассматриваться в качестве эталонного давления. Если предположить, что для идеальной жидкой смеси в контакте с газом константа Генри равна давлению насыщенного пара psat, то уравнение 2.207 также имеет следующий вид:
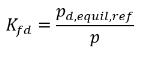
уравнение 2.208
где pd,equil,ref - ссылочное давление для растворенной равновесной массовой доли. Тогда уравнение 2.204 можно переписать следующим образом:
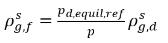
уравнение 2.209
В уравнении 2.202 и уравнении 2.203 переменные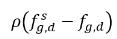 
и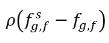 
представляют различия/градиенты концентрации масс, которые определяют поглощение/растворение и выделение неконденсирующихся газов. Это показывает, что для переноса неконденсирующегося газа через две фазы требуется отклонение концентрации массы от ее равновесного состояния. Направление переноса массы может способствовать приближению системы к состоянию равновесия в зависимости от локальных концентраций масс и их равновесия в обеих фазах. Из модели равновесия можно получить следующий результат:
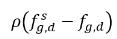и 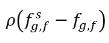представляют различия/градиенты концентрации масс, которые определяют поглощение/растворение и выделение неконденсирующихся газов. Это показывает, что для переноса неконденсирующегося газа через две фазы требуется отклонение концентрации массы от ее равновесного состояния. Направление переноса массы может способствовать приближению системы к состоянию равновесия в зависимости от локальных концентраций масс и их равновесия в обеих фазах. Из модели равновесия можно получить следующий результат:◦ Поглощение/растворение газа в жидкости - имеет место перенос массы из газовой фазы (свободный газ) в жидкую фазу (растворенный газ). Модель равновесия предполагает, что свободный газ в газовой фазе находится в состоянии равновесия: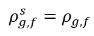 
. Используя уравнение 2.204 и уравнение 2.209, получаем следующий результат:
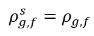. Используя уравнение 2.204 и уравнение 2.209, получаем следующий результат: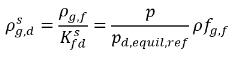
уравнение 2.210
Из уравнения 2.202 и уравнения 2.203 характеристики источника переноса массы имеют следующий вид:
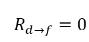
уравнение 2.211
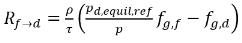
уравнение 2.212
◦ Выделение газа из жидкости - имеет место перенос массы из жидкой фазы (растворенный газ) в газовую фазу (свободный газ). В этом процессе модель равновесия предполагает, что растворенный газ в жидкой фазе всегда находится в состоянии равновесия: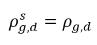 
. Из уравнения 2.202, уравнения 2.203, уравнения 2.204 и уравнения 2.209 скорости переноса массы имеют следующий вид:
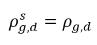. Из уравнения 2.202, уравнения 2.203, уравнения 2.204 и уравнения 2.209 скорости переноса массы имеют следующий вид: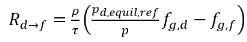
уравнение 2.213
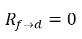
уравнение 2.214
Отметим, что при растворении части неконденсирующегося газа в жидкости свободно расширяющийся газ является единственной частью, остающейся в газовой фазе, fg,f. Следовательно, плотность смеси вычисляется следующим образом:
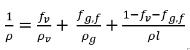
уравнение 2.215
и объемная доля свободного газа имеет следующий вид:
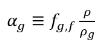
уравнение 2.216