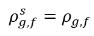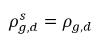캐비테이션 모델의 이론
증기 운송 방정식 2.169에서 Re 및 Rc는 캐비테이션 흐름에서 증기 기포의 성장 및 축소에 연결된 질량 전달 소스 항입니다. 이러한 항은 캐비테이션 프로세스 동안 증기 위상과 액체 위상 간 질량 교환에 대해 계산합니다. Re 및 Rc는 액체의 단일 증기 기포 성장을 설명하는 Rayleigh-Plesset 방정식에서 모델링됩니다.
액체-증기 질량 운송
캐비테이션의 순 위상 변화율에 대한 표현식을 파생하려면 비응축 기체가 고려되지 않는 제로 슬립 속도의 비압축성 액체-증기 2상 흐름을 고려합니다. 액체에서 증기로의 순 질량 전달 속도를 나타내는 R을 도입하면 다음과 같이 액체 및 증기 부피 분율 방정식과 총 질량 연속성 방정식이 제공됩니다.
• 액체 위상
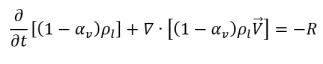
방정식 2.179
• 증기 위상
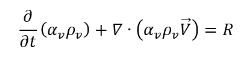
방정식 2.180
• 혼합물(총 질량 연속성)
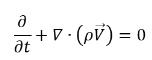
방정식 2.181
액체-증기 2상 시스템에서 혼합물 밀도 ρ는 증기 부피 분율 및 위상 밀도를 기준으로 표현됩니다.
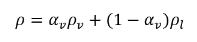
방정식 2.182
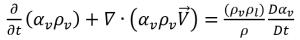
방정식 2.183
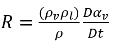
방정식 2.184
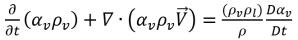
방정식 2.185
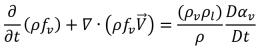
방정식 2.186
방정식 2.185 및 방정식 2.186에서는 액체 위상과 증기 위상 간에 속도 슬립이 0인 조건하에서 캐비테이션이 추가 증기 질량 분율 운송 방정식이 포함된 단상 흐름으로 또는 액체-증기 질량 전달이 포함된 Eulerian 다상 혼합물 흐름으로 모델링됩니다. 확산 및 위상 속도 차이의 효과를 고려하지 않는다면 이 두 접근 방식이 수학적으로 동일합니다. Creo Flow Analysis는 단상 접근 방식을 사용하여 캐비테이션 흐름을 모델링합니다.
기포 역학 고려 사항
대부분의 자연 발생 및 엔지니어링 시스템의 경우 캐비테이션 발생을 위해 액체에 기포, 비응축 기체 등과 같은 핵이 적절하게 존재합니다. 따라서 캐비테이션 프로세스를 모델링하기 위해서 주로 기포 성장 및 축소를 올바르게 계산하는 데 중점을 둡니다. 흐르는 액체에서 액체 기포와 증기 기포 간에 속도 슬립을 0으로 가정하면 액체에서의 기체 기포 성장을 설명하는 일반화된 Rayleigh-Plesset 방정식에서 기포 역학 방정식이 파생됩니다.
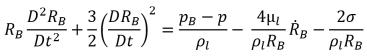
방정식 2.187
여기서 각 항목은 다음을 나타냅니다.
RB | 기포 반지름 |
pB | 기포 압력(다른 기체가 없을 때 액체 온도에서 증기 압력으로 가정됨) |
p | 기포를 둘러싼 액체의 압력 |
σ | 액체와 증기 간 표면 장력 계수 |
이 방정식은 역학적 균형(기포 성장에 대한 열 장벽이 없음)에서 파생됩니다.
2차 주문 시간 유도체(낮은 진동 주파수에 적합), 점성 감쇠 항 및 표면 장력을 무시하면 점근 상태에 유효한 방정식 2.187의 축소된 표현식을 갖습니다.
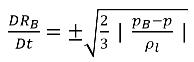
방정식 2.188
이 축소된 Rayleigh-Plesset 방정식은 기포 역학의 효과를 캐비테이션 모델에 도입하는 물리적 접근 방식을 제공합니다. 기포 반지름은 (pB–p)의 부호에 따라 증가하거나 감소합니다. p<pB이면 기포가 성장하고, p>pB이면 기포가 축소합니다. 따라서 방정식 2.188이 다음과 같이 다시 작성됩니다.
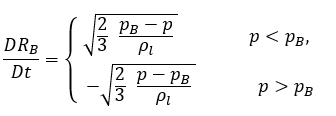
방정식 2.189
η이 액체 내 증기 기포 수 밀도(단위 부피당 존재하는 기포 수)이고, 모든 증기 기포가 반지름이 RB로 동일한 완벽한 구이면 증기 위상 부피 분율이 다음과 같습니다.
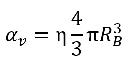
방정식 2.190
액체에서는 증기 기포를 생성하거나 파괴할 수 없지만 캐비테이션 프로세스에서는 이러한 기포가 증가(증발) 및 축소(응결)할 수 있다고 가정합니다. 방정식 2.190에서는 증기 기포 수 밀도(η)가 상수를 유지하지만 기포 반지름(RB)은 증가하거나 감소합니다. 그러면 증기 부피 분율의 시간 도함수가 다음과 같이 계산됩니다.
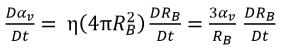
방정식 2.191
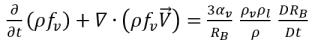
방정식 2.192
방정식 2.189를 적용하면 액체와 증기 간 단위 부피당 순 질량 전달 속도의 형식은 다음과 같습니다.
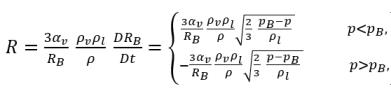
방정식 2.193
여기서 방정식 2.193은 캐비테이션에서 단위 부피 질량 전달 속도(R)가 증기 위상 밀도와 액체 위상 밀도 모두의 함수(비례)이며 혼합물 밀도에 반비례하기도 함을 나타냅니다. 방정식 2.192는 위상 및 혼합물 질량 연속성에서 직접 파생되므로, 이는 정확하고 캐비테이션에서 액체 위상과 증기 위상 간 질량 전달을 정확하게 나타내야 합니다. 기포 역학 도입에 따라 방정식 2.193은 서로 반대되고 물리적으로 서로 다른 두 가지 질량 전달 프로세스(액체에서 증기로(기포 성장 또는 증발), 증기에서 액체로(기포 축소 또는 응결))를 모델링하는 유사한 접근 방식을 사용합니다. 증기 질량 분율 운송 방정식 2.192의 경우 기포 성장이 소스 항이고, 기포 축소가 싱크 항으로 처리됩니다.
실제 캐비테이션 모델에서 국소 원거리장 압력 p는 일반적으로 셀 센터 압력과 동일하게 사용됩니다. 기포 압력 pB는 용존 기체, 질량 운송 및 점성 감쇠가 없는 상태에서 포화 증기 압력(psat, 재료 특성)과 같습니다. pB=psat
• 국소 흐름 압력이 포화 증기 압력보다 낮으면(p<psat) 다음이 되도록 증발만 발생합니다.
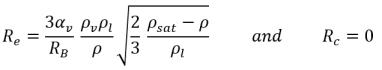
방정식 2.194
• 국소 흐름 압력이 포화 증기 압력보다 높으면(p>psat) 응결만 발생합니다.
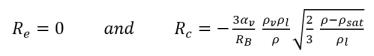
방정식 2.195
방정식 2.194 및 방정식 2.195는 거의 모든 사용 가능 역학적 2상 캐비테이션 모델의 기반이 됩니다. Creo Flow Analysis는 Singhal et al 모델링 접근 방식을 사용합니다.
기체 흡수/용해 및 배출
비응축 기체는 작동 유체에 종종 존재하며 캐비테이션에 상당한 영향을 줄 수 있습니다. 때로는 비응축 기체가 흐름과 함께 자유롭게 운송되며, 액체에 용해되거나 액체에서 배출되기도 하므로 자연스럽게 액체 위상과 기체 위상 간 질량 농도의 동적 평형을 이룹니다. 액체에서의 기체 흡수 또는 용해 및 배출은 액체-기체 질량 전달 현상이기도 하며 이러한 현상은 질량 농도 차이 및 구배에 의해 제어됩니다. 캐비테이션 흐름을 모델링하려면 혼합물 흐름에서 비응축 기체 및 가능한 액체-기체 질량 전달의 효과에 대해 계산해야 할 수도 있습니다.
액체-기체 2상 흐름의 액체 위상(용존 기체)과 기체 위상(자유 기체) 모두에 공기 또는 산소와 같은 비응축 기체가 존재한다는 가정하에서 각 위상의 기체 질량 분율 운송 방정식은 다음과 같습니다.
• 자유 기체(기체 위상)
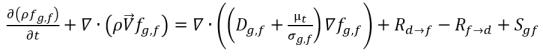
방정식 2.196
• 용존 기체(액체 위상)
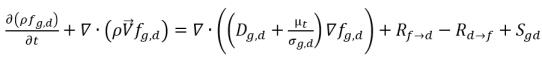
방정식 2.197
여기서 각 항목은 다음을 나타냅니다.
fg,f | 자유 기체의 질량 분율 |
fg,d | 자유 기체 및 용존 기체의 질량 분율 |
Sg,f, Sg,d | 외부 또는 사용자 정의 소스 |
Dg,f | 자유 기체 및 용존 기체의 확산도 |
Dg,d | 용존 기체의 확산도 |
비응축 기체의 질량 분율이 fg로 사전 설명되면 다음이 제공됩니다.
fg=fg,f
또는 공간 및 시간에서의 해당 운송은 다음 방정식을 풀어서 구합니다.
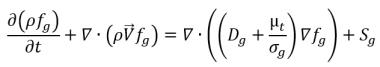
방정식 2.199
두 위상이 접촉하면 두 위상 간의 동적 평형을 달성하기 위해 자유 기체 f 및 용존 기체 d가 하나의 위상에서 다른 위상으로 운송하는 기질이 있습니다. 평형 모델에서는 질량 전달의 부피 속도가 질량-농도 구배 또는 차이에 따라 달라진다고 가정합니다.
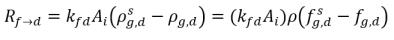
방정식 2.200
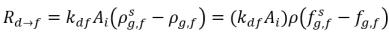
방정식 2.201
여기서 각 항목은 다음을 나타냅니다.
AI | 액체-기체 계면 면적 |
kf,d(=kd,f) | 대량 부피 질량 전달 계수 |
ρg,d(=ρfg,d) | 용존 기체의 국소 질량 농도 |
ρg,f(=ρfg,f) | 자유 기체의 국소 질량 농도 |
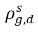 | 용존 기체의 해당 호스팅 위상에 대한 평형 질량 농도 |
 | 자유 기체의 해당 호스팅 위상에 대한 평형 질량 농도 |
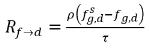
방정식 2.202
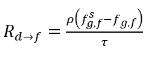
방정식 2.203
일반적으로 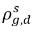 및
및 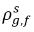 는 동일하지 않습니다(불연속성). 두 농도 간 잘 정의된 평형 커브가 있으며 이는 온도, 압력 및 혼합물 구성에 따라 달라집니다. 커브는 일반적으로 단조 및 비선형이며 종종
는 동일하지 않습니다(불연속성). 두 농도 간 잘 정의된 평형 커브가 있으며 이는 온도, 압력 및 혼합물 구성에 따라 달라집니다. 커브는 일반적으로 단조 및 비선형이며 종종 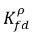 계수의 준선형 관계식으로 표현됩니다.
계수의 준선형 관계식으로 표현됩니다.
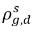 및
및 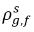 는 동일하지 않습니다(불연속성). 두 농도 간 잘 정의된 평형 커브가 있으며 이는 온도, 압력 및 혼합물 구성에 따라 달라집니다. 커브는 일반적으로 단조 및 비선형이며 종종
는 동일하지 않습니다(불연속성). 두 농도 간 잘 정의된 평형 커브가 있으며 이는 온도, 압력 및 혼합물 구성에 따라 달라집니다. 커브는 일반적으로 단조 및 비선형이며 종종 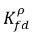 계수의 준선형 관계식으로 표현됩니다.
계수의 준선형 관계식으로 표현됩니다.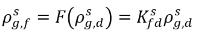
방정식 2.204
여기서 Kf,d는 일반적으로 물리 법칙 또는 상관 관계식을 사용하여 결정됩니다. 한 가지 일반적인 접근 방식은 일반화된 평형 관계를 제공하는 헨리의 법칙을 따르는 것입니다. 이는 기체 위상과 접촉하는 액체 혼합물의 경우 자유 기체의 부분 압력인 ρg,f가 액체 위상에서 용존 기체의 평형 몰 분율 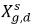 와 헨리 상수 Hx의 곱과 같음을 나타냅니다.
와 헨리 상수 Hx의 곱과 같음을 나타냅니다.
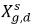 와 헨리 상수 Hx의 곱과 같음을 나타냅니다.
와 헨리 상수 Hx의 곱과 같음을 나타냅니다.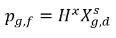
방정식 2.205
자유 기체 위상이 이상 기체 법칙을 따르면 부분 압력의 돌턴의 법칙이 다음 방정식을 제공합니다.
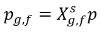
방정식 2.206
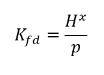
방정식 2.207
따라서 헨리의 상수는 압력 단위를 가지며 기준 압력으로 고려될 수 있습니다. 기체와 접촉하는 이상 액체 혼합물의 경우 헨리의 상수가 포화 증기 압력 psat라고 가정하면 다음과 같은 방정식 2.207도 제공됩니다.
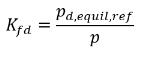
방정식 2.208
여기서 pd,equil,ref는 용존 평형 질량 분율에 대한 기준 압력입니다. 그러면 방정식 2.204가 다음으로 다시 작성됩니다.
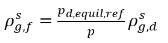
방정식 2.209
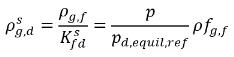
방정식 2.210
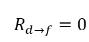
방정식 2.211
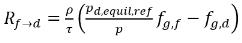
방정식 2.212
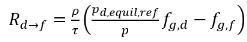
방정식 2.213
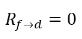
방정식 2.214
비응축 기체의 일부가 액체로 용해되면 자유롭게 팽창 가능한 기체만 기체 위상 fg,f에 남아 있는 부분입니다. 따라서 혼합물 밀도가 다음으로 계산됩니다.
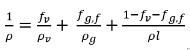
방정식 2.215
그리고 자유 기체의 부피 분율은 다음과 같습니다.
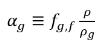
방정식 2.216
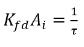 에 질량 전달 효율의 표시인 역한시 단위(1/s)가 지정됩니다. 따라서
에 질량 전달 효율의 표시인 역한시 단위(1/s)가 지정됩니다. 따라서 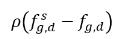 및
및 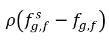 는 비응축 기체의 흡수/용해 및 배출의 구동력인 질량 농도 차이/구배입니다. 이는 두 위상 간에 비응축 기체 운송 시 질량 농도를 해당 평형 상태에서 분리해야 함을 나타냅니다. 질량 전달 방향은 두 위상 모두에서의 국소 및 평형 질량 농도에 따라 시스템을 평형 방향으로 이동합니다. 평형 모델에서 다음을 사용할 수 있습니다.
는 비응축 기체의 흡수/용해 및 배출의 구동력인 질량 농도 차이/구배입니다. 이는 두 위상 간에 비응축 기체 운송 시 질량 농도를 해당 평형 상태에서 분리해야 함을 나타냅니다. 질량 전달 방향은 두 위상 모두에서의 국소 및 평형 질량 농도에 따라 시스템을 평형 방향으로 이동합니다. 평형 모델에서 다음을 사용할 수 있습니다.