지배 방정식
캐비테이션 운송 모델에서 액체 및 기체(증기 및 다른 가능한 기체) 혼합물의 체적 운동은 가변 밀도 단상 흐름으로 처리됩니다. 혼합물 흐름에 대한 일반 지배 방정식 세트는 다중 컴포넌트 흐름에 대한 해당 세트와 동일하고, 운송 방정식은 캐비테이션에서 생성된 증기 질량 분율을 지배하도록 구체적으로 형성됩니다. 비응축 기체의 효과를 모델링하기 위해 기체 모델에 따라 기체 질량 분율에 대한 추가 운송 방정식의 해를 구할 수도 있습니다. 캐비테이션 흐름에 대한 해를 구한 일반 지배 방정식의 전체 세트는 다음과 같습니다.
• 연속성
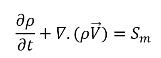
방정식 2.166
여기서 Sm은 캐비테이션과 독립적인 순 외부 또는 사용자 소스입니다.
• 운동량 방정식
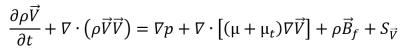
방정식 2.167
• 에너지 방정식
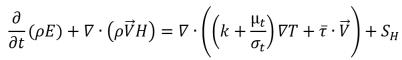
방정식 2.168
• 증기 질량 분율 방정식
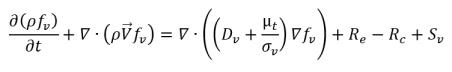
방정식 2.169
여기서 각 항목은 다음을 나타냅니다.
fv | 증기 질량 분율 |
Re | 증기 생성 소스(증발) |
Rc | 싱크 항(응결) |
Sv | 외부 또는 사용자 정의 증기 소스 항 |
• 비응축 기체(NCG) 질량 분율 방정식
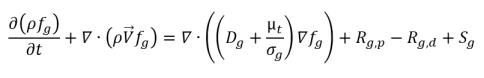
방정식 2.170
이는 생성, 싱크 및 외부 소스 또는 사용자 정의 소스 항을 포함한 비응축 기체(NCG)에 대한 일반 운송 방정식입니다.
캐비테이션 모델에 따라 비응축 기체, 용존 기체 등으로 서로 다른 방정식(0과 2 사이)이 풀립니다.
터뷸런스 흐름의 경우 터뷸런스 모델링 방정식을 풀어 터뷸런스 점도 μt를 구합니다. 터뷸런스 Prandtl 수 σt, σv, σ g는 사전 설명된 모델 매개 변수입니다. 터뷸런스 모델의 세부 내용은 터뷸런스(Turbulence) 모듈에서 제공됩니다.
운송 방정식에서 혼합물 특성은 다음 관계식을 사용하여 계산됩니다.
• 혼합물 밀도
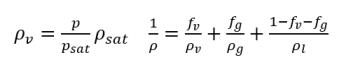
방정식 2.171
여기서 각 항목은 다음을 나타냅니다.
ρv | 증기 밀도 |
ρg | 비응축 자유 기체 밀도 |
ρl | 액체 밀도 |
액체 밀도와 증기 밀도는 상수(비압축성), 변수(압축성) 중 하나 또는 둘 다일 수 있습니다. 그러나 비응축 자유 기체 밀도는 캐비테이션 모델에서 항상 이상 기체로 간주됩니다. 방정식 2.171에서 액체 질량 분율 ƒl은 다음과 같이 물리적 제약 조건(단위로 계산되는 모든 컴포넌트의 질량 분율)을 사용하여 계산됩니다.
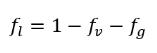
방정식 2.172
캐비테이션 흐름에서 관심 있는 매개 변수는 증기 αv 또는 전체 기체-위상 부피 분율 αtotal입니다. 이는 풀이된 질량 분율 ƒv 및 자유 기체 질량 분율 ƒg에서 추론됩니다.

방정식 2.173
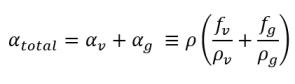
방정식 2.174
• 혼합물 점도
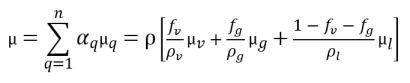
방정식 2.175
여기서 각 항목은 다음을 나타냅니다.
μv | 증기의 동적 점도 |
μg | 비응축 자유 가스 |
μl | 액체 |
• 혼합물 열 특성
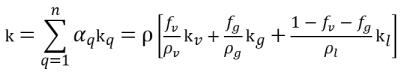
방정식 2.176
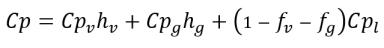
방정식 2.177
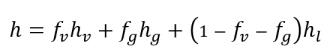
방정식 2.178
여기서 각 항목은 다음을 나타냅니다.
k | 열 전도성 |
Cp | 일정 압력 프로세스에 대한 비열 |
h | 비엔탈피 |
관련된 컴포넌트는 해당되는 아래 첨자인 v(증기의 경우), g(비응축 자유 기체의 경우) 및 l(액체의 경우)로 표시됩니다.