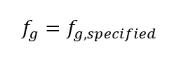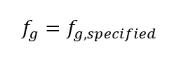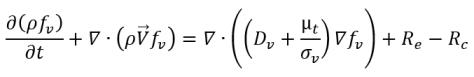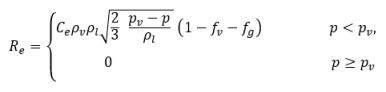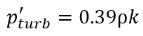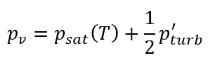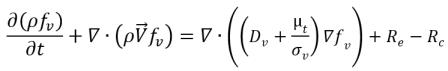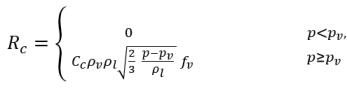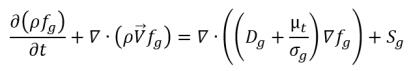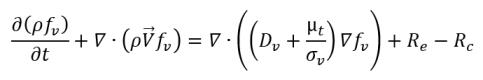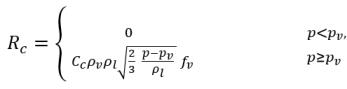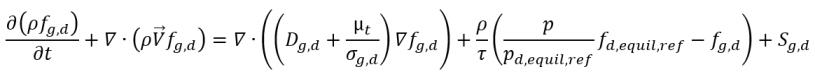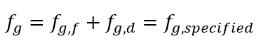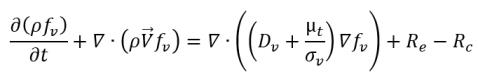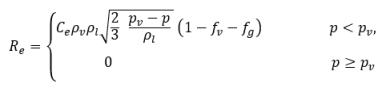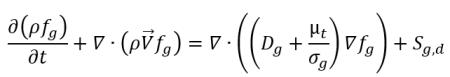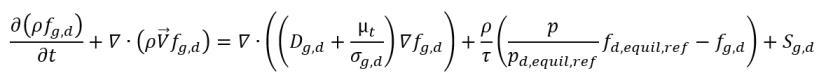Модели кавитации
В Creo Flow Analysis, как и в первоначальной модели Сингхала и др., предполагается, что рабочая жидкость в потоках с кавитацией всегда является смесью жидкости, пара и некоторых неконденсирующихся газов. По умолчанию в моделях кавитации учитывается фазовый переход жидкость-пар и эффект неконденсирующихся газов. На основе подхода к моделированию для учета неконденсирующегося газа в следующей таблице представлены пять различных моделей для прогнозирования аэрации и кавитации в жидкой системе. Эти модели подробно описаны в данном разделе.
|
Модели для неконденсирующегося газа
|
Описание
|
|
Постоянная массовая доля газа
|
Массовая доля неконденсирующегося газа (НКГ) является постоянной и исключается из решения с крошечными сжимаемыми пузырьками.
|
|
Переменная массовая доля газа
|
Аналогична модели постоянной массовой доли газа, но массовая доля неконденсирующегося газа может изменяться, поскольку на входные отверстия могут поступать различные массовые доли.
|
|
Модель равновесного растворенного газа
|
Массовая доля неконденсирующегося газа, растворенного в жидкости, равняется равновесному значению.
|
|
Модель растворенного газа
|
Массовая доля неконденсирующегося газа (НКГ), растворенного в жидкости, зависит от уровня абсорбции или десорбции и равновесного значения.
|
|
Полная газовая модель
|
Комбинирует модели растворенного газа и переменной массовой доли газа.
|
Модель постоянной массовой доли газа
Модель постоянной массовой доли газа является базовой или моделью кавитации по умолчанию в Creo Flow Analysis. Она основывается на работе Сингхала и др. В этой модели предполагается, что в рабочей жидкости присутствующий неконденсирующийся газ в жидкости является нерастворимым газом и образует пузырьки газа, для которых действуют законы идеального газа. Хотя весь предварительно описанный неконденсирующийся газ может свободно расширяться с уменьшением давления в зонах кавитации, массовая доля неконденсирующихся газов задается предварительно и остается той же в потоке с кавитацией:
уравнение 2.217
где fg,specified - определенное пользователем значение.
Плотность неконденсирующегося газа следует закону идеального газа:
уравнение 2.218
где T - температура жидкости, которая может быть предварительно задана (изотермический поток) или получена в решении
уравнения 2.168 для сохранения энергии смеси, когда учитывается теплопроводность. Из
уравнения 2.173 следует объемная доля неконденсирующегося газа:
уравнение 2.219
Хотя массовая доля неконденсирующегося газа зафиксирована и обычно имеет малое значение 1.5e-05, или 15 миллионных долей в природной воде, ее объемная доля αg изменяется и может иметь более высокое значение. В полостях или зонах низкого давления неконденсирующийся газ конкурирует с паром при заполнении пустот в пространстве в зависимости от плотностей пара и газа.
Для переноса массы жидкого пара
уравнение 2.194 и
уравнение 2.195 служат основой для построения источника кавитации и члена стока в
уравнении 2.169 для массовой доли пара. В частности, радиус пузырька R
B должен быть рассчитан с использованием известных количественных величин потока во время роста и во время коллапса пузырьков.
Сингхал и др. утверждали, что если типичный размер пузырьков R
B совпадает с ограничивающим (максимальным возможным) размером пузырьков, то R
B определяется балансом между силами аэродинамического сопротивления и поверхностного натяжения. Корреляция, обычно используемая в ядерной отрасли:
уравнение 2.220
где Vrel - величина относительной скорости жидкости и пара. В режиме потока с пузырьками, в котором происходит кавитация, Vrel обычно является малой (примерно 5-10 % от скорости жидкости). С использованием различных ограничивающих аргументов (таких как RB → 0, когда αv → 0) и того факта, что скорости фазовых переходов на единицу объема должны быть пропорциональны объемным долям (или массовым долям) донорской фазы, получаются следующие выражения для скоростей производства и конденсации пара, завершающие модель кавитации:
уравнение 2.221
уравнение 2.222
уравнение 2.223
где C
e и C
c - коэффициенты парообразования и конденсации, которые могут быть определенными пользователями постоянными значениями, для которых по умолчанию задаются значения 1.0, или функциями известных количественных параметров потока. В
уравнении 2.222 и
уравнении 2.223 вводится новое пороговое давление ρ
v для замены давления насыщенного пара ρ
sat в
уравнении 2.194 и
уравнении 2.195. Согласно методу
Сингхала и др., для расчета влияния турбулентности на потоки с кавитацией, наблюдаемого в экспериментальных исследованиях, используется локальное значение колебаний турбулентного давления, введенное
Хинце:
уравнение 2.224
добавляется к давлению насыщенного пара, чтобы повысить пороговое значение давления фазового перехода до:
уравнение 2.225
Для ламинарного потока pv=psat(T)
Когда учитывается теплопередача и изменения всех фазовых плотностей (включая жидкость, пар и неконденсирующиеся газы) с температурой, давление насыщенного пара psat также является функцией температуры. Следовательно, прямое влияние температуры на кавитацию может учитываться в этой модели кавитации.
Модель переменной массовой доли газа
В модели переменной массовой доли газа предполагается, что неконденсирующийся газ всегда остается свободным газом, который не может растворяться в жидкости, но его массовая доля больше не является предварительно заданной константой, как в модели постоянной массовой доли газа. Вместо этого распределение локальной массовой доли определяется транспортным уравнением. Тогда как передача массы жидкого пара моделируется той же моделью кавитации, используемой в
уравнении 2.221,
уравнении 2.222 и
уравнении 2.223. Для ясности ниже приводится полный набор уравнений модели:
• Фазовый переход жидкость-пар
уравнение 2.226
где:
уравнение 2.227
уравнение 2.228
• Транспортное уравнение неконденсирующегося газа
Следующее
уравнение 2.229 представляет транспортное уравнение для неконденсирующегося газа (f
g):
уравнение 2.229
где Sg - внешний или определяемый пользователем источник для неконденсирующегося газа.
Модель равновесного растворенного газа
В потоках с кавитацией неконденсирующиеся газы (НКГ) растворяются в жидкости или выделяются из нее для достижения динамического равновесия массовых концентраций между жидкими и газовыми фазами. В модели равновесного растворенного газа предполагается, что массовая доля всего неконденсирующегося газа остается постоянной. Однако часть его растворяется в жидкости, чтобы мгновенно удовлетворить условие локального равновесия. Математически, в дополнение к тому же уравнению для массовой доли пара и моделям переноса массы пара, решается дополнительное транспортное уравнение для массовой доли растворенного газа fgd, в котором предполагается, что всегда имеет место состояние равновесия. Уравнения моделирования имеют следующий вид:
• Фазовый переход жидкость-пар
уравнение 2.230
где:
уравнение 2.231
уравнение 2.232
• Поглощение и выделение газа
уравнение 2.233
где:
Sg,d | определяемый пользователем закон растворения и выделения газа |
fd,equil,ref | равновесная массовая доля растворенного газа при эталонном давлении pd,equil,ref |
fd,equil,ref и pd,equil,ref | - определенные пользователями значения |
В этой модели равновесия временная шкала Γ приближается к нулю, и перенос массы является практически мгновенным. Отметим, что в
уравнении 2.231 свободный газ имеет массовую долю f
g,f вместо f
g. Массовая доля свободного газа получается из условия:
уравнение 2.234
где fg,specified - определенное пользователем значение.
Модель растворенного газа
В этой модели опускается условие, что растворенный газ в жидкости всегда находится в состоянии равновесия. Вместо того чтобы определяться условием равновесия с мгновенным переносом массы, массовая доля растворенного газа (f
g,d) зависит от транспорта компонента и скорости растворения или выделения газа (конечная скорость). Поэтому в модели растворенного газа используются те же формулы моделирования, что и в модели равновесного растворенного газа,
уравнение 2.230 -
уравнение 2.234. Однако конечные уровни переноса массы для растворения и выделения газа характеризуются другим масштабом времени (Γ). Для поглощения или растворения газа в жидкости Γ задается указанным временем поглощения (время растворения газа по умолчанию равняется 10 с). Для выделения растворенного газа из жидкости скорость переноса массы задается указанным временем выделения газа (время выделения растворенного газа Γ по умолчанию равняется 10 с).
Полная газовая модель
Полная газовая модель является комбинацией модели растворенного газа и переменной газовой модели. Массовая доля неконденсирующегося газа изменяется во времени и пространстве, тогда как растворение газа или поглощение и выделение также могут иметь место для неконденсирующихся газов. Полный набор уравнений моделирования приведен ниже:
• Фазовый переход жидкость-пар
уравнение 2.235
где:
уравнение 2.236
уравнение 2.237
• Транспорт неконденсирующегося газа
уравнение 2.238
• Поглощение и выделение газа
уравнение 2.239