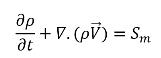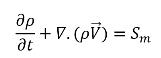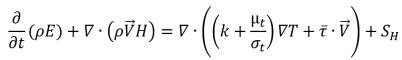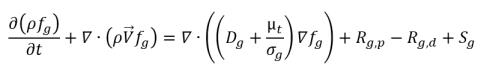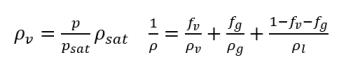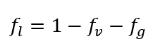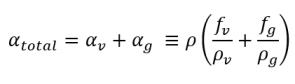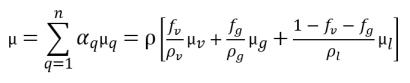Основные уравнения

В кавитационных транспортных моделях объемное движение смеси жидкости и газа (пар и другие возможные газы) обрабатывается как однофазный поток переменной плотности. Набор главных основных уравнений для потока смеси совпадает с набором для многокомпонентных потоков, тогда как транспортное уравнение специально формируется, чтобы описывать массовую долю пара, созданную в кавитации. Чтобы смоделировать эффекты неконденсирующихся газов, дополнительные транспортные уравнения для газовых массовых долей также могут решаться в зависимости от газовых моделей. Полный набор главных основных уравнений, решаемых для потоков с кавитацией:

fv	массовая доля пара
Re	источник создания пара (испарение)
Rc	член стока (конденсация)
Sv	внешний или определяемый пользователем член источника пара

Это главное транспортное уравнение для неконденсирующихся газов (НКГ), включающее члены генерирования, стока и внешних или пользовательских источников.

В зависимости от кавитационных моделей различные уравнения (от нуля до двух) решаются как неконденсирующийся газ, растворимый газ и т. д.

Для турбулентных течений турбулентная вязкость μt получается из решения уравнений моделирования турбулентности. Турбулентные числа Prandtl σt, σv и σg являются предварительно заданными параметрами модели. Подробная информация о моделях турбулентности предоставлена в модуле Турбуленция (Turbulence).

В транспортных уравнениях свойства смеси рассчитываются с помощью следующих уравнений:

Плотности жидкости и пара рассматриваются как постоянные (несжимаемые), переменные (сжимаемые) или и те и другие. Однако плотность неконденсирующегося свободного газа в моделях кавитации всегда рассматривается как идеальный газ. Отметим, что в уравнении 2.171 массовая доля жидкости ƒl рассчитывается с помощью физического ограничения: массовые доли всех компонентов в сумме должны давать единицу, как видно ниже:

В потоках с кавитацией представляет интерес параметр пара αv или общая объемная доля газовой фазы αtotal, которая рассчитывается из решения для массовой доли ƒv и массовой доли свободного газа ƒg.

Включенные компоненты обозначаются с определенными нижними индексами для пара (v), неконденсирующегося свободного газа (g) и жидкости (l).

ρv	плотность пара
ρg	плотность неконденсирующегося свободного газа
ρl	плотность жидкости

μv	динамическая вязкость пара
μg	неконденсирующийся свободный газ
μl	жидкость

k	теплопроводность
Cp	удельная теплоемкость для процесса с постоянным давлением
h	удельная энтальпия