Creo Flow Analysis > Pre-elaborazione > Definizione della fisica > Turbolenza > Fisica > Modelli di turbolenza
  
Modelli di turbolenza
È possibile calcolare la viscosità turbolenta effettiva in un sistema di fluidi in base al modello di viscosità turbolenta. Il modello di viscosità turbolenta include due modelli.
• Modello k-epsilon standard
Il modello k-epsilon standard è un modello di Turbolenza (Turbulence) disponibile in Creo Flow Analysis.
La formulazione per l'energia cinetica turbolenta k è:
La formulazione per il tasso di dissipazione turbolenta ε è:
Dove
c1=1.44
Costanti C1
c2=1.92
costanti C2
σk=1
Numero di Prandtl dell'energia cinetica turbolenta
σz=1
Numero di Prandtl del tasso di dissipazione della turbolenza
Energia cinetica turbolenta
v’
Velocità di fluttuazione turbolenta
Tasso di dissipazione dell'energia turbolenta
Tensore di deformazione
u’i(i=1,2,3)
Componenti della velocità di fluttuazione turbolenta
Viscosità turbolenta, con Cμ=0.09 e E=9.793
Termine della generazione di turbolenza
Tensione di Reynolds della turbolenza
Approssimazione di Boussinesq per la tensione di Reynolds
Riferimenti: Launder, B.E. & Spalding, D.B. (1974) "The numerical computation of turbulent flows" Computer Methods, Applied Mechanics and Engineering, vol. 3, pp. 269-289
• Modello k-epsilon del gruppo di rinormalizzazione (RNG)
Il modello k-epsilon del gruppo di rinormalizzazione (RNG) è un modello di Turbolenza (Turbulence) disponibile in Creo Flow Analysis. Questo modello è simile al modello k-epsilon standard ma con un'espressione che coinvolge due nuove costanti che vengono utilizzate per modificare il termine RNG C2 nell'equazione riportata di seguito.
Dove
η0=4.38
Costante RNG (codificata in Flow Analysis)
β=1.92
Costante RNG (codificata in Flow Analysis)
P
Pressione locale
c1=1.44
Costanti C1
c2=1.92
costanti C2
σk=1
Numero di Prandtl dell'energia cinetica turbolenta
σz=1
Numero di Prandtl del tasso di dissipazione della turbolenza
Energia cinetica turbolenta
v’
Velocità di fluttuazione turbolenta
Tasso di dissipazione dell'energia turbolenta
Tensore di deformazione
u’i(i=1,2,3)
Componenti della velocità di fluttuazione turbolenta
Viscosità turbolenta, con Cμ=0.09
Termine della generazione di turbolenza
Tensione di Reynolds della turbolenza
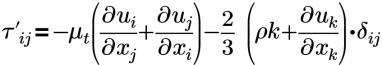Approssimazione di Boussinesq per la tensione di Reynolds
Riferimenti: Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. & Speziale, C.G. (1992), "Development of turbulence models for shear flows by a double expansion technique", Phys. of Fluids A, Vol. 4, No. 7, pp 1510-1520