Considerazioni speciali del modello VOF (volume di fluido)
Modello VOF e modello di miscela
Nell'approccio di modellazione multifase euleriano omogeneo, sia il modello VOF (volume di fluido) che il modello euleriano della miscela risolvono la stessa serie di equazioni governanti (alla media) della miscela. Tuttavia, si basano su meccanismi fisici diversi e pertanto vengono applicate a diversi regimi di flusso multifase.
• Modello di miscela - Progettato per due o più fasi (fluida o di polveri), che vengono considerate come un continuo di compenetrazione. Risolve l'equazione del momento della miscela e le equazioni di energia e l'interfaccia fase-fase non viene tracciata o non vengono osservate interfacce chiare. Le applicazioni del modello di miscela includono flussi carichi di particelle a bassi carico, flussi di bolle e goccioline, sedimentazione e filtri a ciclone. Potete utilizzare il modello di miscela anche con le velocità relative prescritte per le fasi disperse per modellare i flussi multifase non omogenei.
• Modello VOF - Generalmente è una tecnica di monitoraggio della superficie temporaneo progettata per due o più fluidi immiscibili dove viene considerata la posizione dell'interfaccia fase-fase. Nel modello VOF, una singola serie di equazioni di momento ed energia è condivisa da tutte le fase e viene risolta in modo implicito. Le frazioni di volume di fase vengono ottenute utilizzando algoritmi temporali espliciti o impliciti molto precisi con schemi di avvezione a ordine elevato per risolvere le interfacce nitide tra una coppia di fasi. Tra le applicazioni tipiche del modello VOF vi sono i flussi stratificati, i flussi di libera superficie, il riempimento, lo sciabordio, il movimento di bolle di grandi dimensioni in un liquido, il movimento di liquido dopo la rottura di una diga, la previsione della rottura del getto (tensione superficiale) e il monitoraggio di tutte le interfacce liquido-gas.
La formulazione VOF si basa sul fatto che due o più fluidi (o fasi) non si compenetrano. In una determinata cella di volume di controllo, quindi, frazioni di volume delle fasi locali possono determinare se la cella contiene solo una delle fasi o una miscela delle due fasi. Ad esempio, per la q-esima fase, se la frazione di volume in una cella è αq, allora sono possibili solo tre condizioni:
◦ αq = 0: la cella non contiene la fase q-esima
◦ αq = 1: la cella contiene la fase q-esima
◦ 0< αq < 1: la cella contiene l'interfaccia tra la q-esima fase e una o più altre fasi.
Di conseguenza, potete eseguire il monitoraggio delle interfacce tra le fasi dalla soluzione di un'equazione di trasporto per la frazione di volume di una o più fasi.
L'effetto della tensione superficiale
La tensione superficiale è la tendenza elastica di una superficie fluida che le consente di sistemarsi nell'area di superficie più piccola possibile. Considerate una bolla di aria in un liquido. Nella bolla, la forza netta su una molecola a causa delle molecole vicine è zero. Sulle interfacce liquido-aria, la tensione superficiale deriva dalla maggior attrazione (tra loro) delle molecole di liquido a causa della coesione che non delle molecole di aria a causa dell'adesione. L'effetto netto è una forza radiale diretta verso l'interno sulla superficie, che provoca la compressione delle bolle. La pressione nella bolla aumenta per controbilanciare la forza attrattiva tra le molecole.
• Il modello di forze superficiali di continuum
In
Creo Flow Analysis, il modello VOF può includere gli effetti della tensione superficiale lungo l'interfaccia tra ciascuna coppia di fasi. Il modello di tensione adottato è basato sul modello Continuum Surface Force (CFS) di Brackbill et al. Questo approccio considera l'effetto della tensione superficiale come forza volumetrica aggiuntiva concentrata sull'interfaccia anziché una forza di superficie. Per l'interfaccia della superficie mostrata nella
figura 2.26 di seguito, il fluido principale è la fase q (la fase liquida) e il fluido secondario è la fase p (in genere, una fase gassosa). A seconda del modello di forze superficiali di continuum, la curvatura della superficie viene calcolata dai gradienti locali normali alla superficie sull'interfaccia. Se
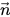
è il vettore normale alla superficie, definito come gradiente della frazione di volume del fluido primario, α
q:
La curvatura dell'interfaccia k viene definita come funzione della divergenza del vettore normale di unità:
equazione 2.93
dove
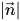
è la grandezza del vettore
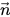
.
La forza della tensione superficiale sulla superficie viene espressa come forza volumetrica mediante il teorema di divergenza, che è una funzione di origine aggiuntiva aggiunta all'equazione del momento della miscela.
equazione 2.94
dove σ
qp è il coefficiente della tensione superficiale tra il fluido q e il fluido p e l'unità è N/m. L'
equazione 2.94 consente una breve sovrapposizione delle forze accanto alle celle quando sono presenti più di due fasi. Se in una cella sono presenti solo due fasi, saranno presenti le seguenti relazioni:
equazione 2.95
dove ρ è la densità della miscela. Quindi l'
equazione 2.94 si riduce a
equazione 2.96
• Inclusione della forza di tensione superficiale
L'importanza degli effetti della tensione superficiale è determinata da due parametri non dimensionali: il numero di Reynolds Re e il numero capillare Ca o il numero di Reynolds e il numero di Weber We:
Se Re<<1, il parametro di interesse è il numero capillare:
equazione 2.97
dove U∞ è la velocità del flusso libero. Gli effetti della tensione superficiale vengono trascurati se Ca>>1, poiché la forza di tensione superficiale è troppo piccola.
Se Re>>1, il parametro di interesse è il numero di Weber:
equazione 2.98
dove la L rappresenta la lunghezza caratteristica. Gli effetti della tensione superficiale possono essere trascurati se We>>1, quando la forza di inerzia è molto maggiore della forza di tensione superficiale.
Adesione della parete (angolo di contatto)
Nel modello di volume di fluido (VOF) è disponibile un'opzione per specificare un angolo di adesione della parete insieme al modello di tensione superficiale. In base a Brackbill et al., invece dell'applicazione di tale condizione al limite direttamente alla parete, l'angolo di contatto tra il fluido e la parete all'interfaccia viene utilizzato per regolare la normale alla superficie nelle celle in prossimità della parete. Questa cosiddetta condizione al limite dinamica provoca la regolazione della curvatura della superficie vicino alla parete.
Se θ è l'angolo di contatto dell'interfaccia della superficie libera sulla parete, come illustrato nella
figura 2.26, allora il vettore normale all'unità sulla cella vicino alla parete viene calcolato come:
equazione 2.99
dove
| vettore unitario normale alla parete |
| vettore unitario tangente alla parete |
Quindi, la velocità normale dell'unità calcolata
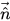
viene utilizzata per determinare la curvatura locale della superficie,
equazione 2.93 e successivamente la forza di tensione superficiale,
equazione 2.94 o
equazione 2.95.
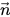 è il vettore normale alla superficie, definito come gradiente della frazione di volume del fluido primario, αq:
è il vettore normale alla superficie, definito come gradiente della frazione di volume del fluido primario, αq: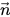 è il vettore normale alla superficie, definito come gradiente della frazione di volume del fluido primario, αq:
è il vettore normale alla superficie, definito come gradiente della frazione di volume del fluido primario, αq:
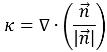
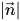 è la grandezza del vettore
è la grandezza del vettore 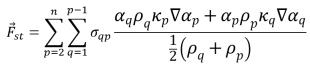
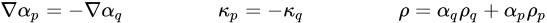
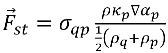
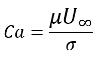
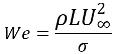

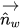
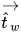
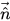 viene utilizzata per determinare la curvatura locale della superficie,
viene utilizzata per determinare la curvatura locale della superficie,