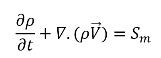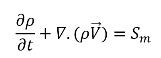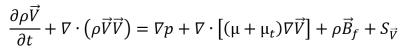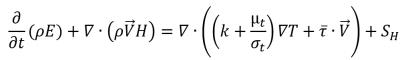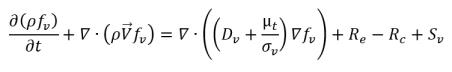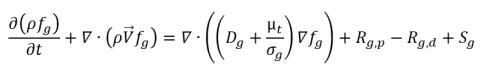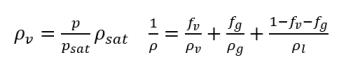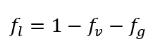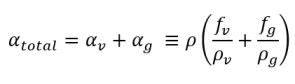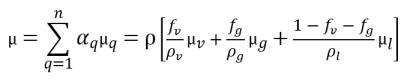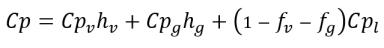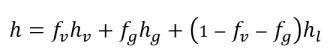Zugrunde liegende Gleichungen
Bei Kavitationstransportmodelle wird die Massenbewegung der Mischung aus Flüssigkeit und Gas (Dampf und andere mögliche Gase) als einphasiger Fluss mit variabler Dichte behandelt. Der Satz der allgemeinen zugrunde liegenden Gleichungen für den Mischungsfluss ist der gleiche wie für Mehrfachkomponentenflüssigkeiten, während eine Transportgleichung speziell für den Dampfmassenanteil gebildet wird, der bei der Kavitation generiert wird. Zur Modellierung der Effekte nicht kondensierbarer Gase können auch zusätzliche Transportgleichungen für Gasmassenanteile abhängig von den Gasmodellen gelöst werden. Der vollständige Satz der allgemeinen zugrunde liegenden Gleichungen, die für Kavitationsflüsse gelöst werden, folgt:
• Stetigkeit
Gleichung 2.166
wobei Sm die resultierende externe Kavitation oder die benutzerquellenunabhängige Kavitation ist
• Impulsgleichungen
Gleichung 2.167
• Energiegleichung
Gleichung 2.168
• Dampfmassenanteil-Gleichung
Gleichung 2.169
Dabei gilt:
fv | Dampfmassenanteil |
Re | Dampferzeugungsquelle (Verdampfung) |
Rc | Senkenfunktion (Kondensation) |
Sv | Externe oder benutzerdefinierten Dampfquellenfunktion |
• Massenanteilgleichung(en) für nicht kondensierbares Gas (NKG)
Gleichung 2.170
Dies ist eine allgemeine Transportgleichung für nicht kondensierbare Gase (NKG), einschließlich Erzeugung, Senken- und externen oder benutzerdefinierten Quellenfunktionen.
Je nach Kavitationsmodellen werden verschiedene Gleichungen (zwischen null und zwei) für nicht kondensierbares Gas, gelöstes Gas usw. gelöst.
Für turbulente Flüsse wird die turbulente Viskosität μ
t durch Lösen der Turbulenzmodellierungsgleichungen ermittelt. Die turbulenten
Prandtl-Zahlen σ
t, σ
v, σ
g sind vorgegebene Modellparameter. Die Details der Turbulenzmodelle sind im Model
Turbulence beschrieben.
In den Transportgleichungen werden die Mischungseigenschaften unter Verwendung der folgenden Beziehungen berechnet:
• Mischungsdichte
Gleichung 2.171
Dabei gilt:
ρv | Dampfdichte |
ρg | Dichte des nicht kondensierbaren freien Gases |
ρl | Flüssigkeitsdichte |
Die Flüssigkeitsdichte und die Dampfdichte sind konstant (inkompressibel), variabel (kompressibel) oder beides. Die Dichte des nicht kondensierbaren freien Gases wird in den Kavitationsmodellen jedoch immer als ideales Gas betrachtet. Beachten Sie, dass in
Gleichung 2.171 der Flüssigkeitsmassenanteil ƒ
l unter Verwendung der physikalischen Randbedingung berechnet wird: Die Massenanteile aller Komponenten summieren sich, wie unten berechnet:
Gleichung 2.172
In Kavitationsflüssen ist der interessierende Parameter der Dampf αv oder der Gesamtgasphasenvolumenanteil αtotal, der aus dem gelösten Massenanteil ƒv und dem freien Massenanteil ƒg abgeleitet wird.
Gleichung 2.173
Gleichung 2.174
• Mischungsviskosität
Gleichung 2.175
Dabei gilt:
μv | Dynamische Viskosität des Dampfes |
μg | nicht kondensierbares freies Gas |
μl | Flüssigkeit |
• Thermische Eigenschaften der Mischung
Gleichung 2.176
Gleichung 2.177
Gleichung 2.178
Dabei gilt:
k | Wärmeleitfähigkeit |
Cp | spezifische Wärme für einen konstanten Druckprozess |
h | spezifische Enthalpie |
Die beteiligten Komponenten werden mit spezifischen tiefgestellten Buchstaben für Dampf (v), nicht kondensierbares freies Gas (g) und Flüssigkeit (l) bezeichnet.