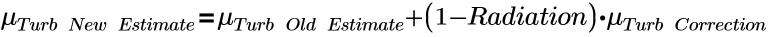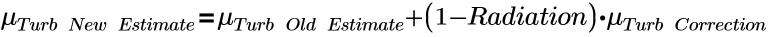Turbulent Viscosity
La
viscosité turbulente est une condition relative à un
Domaine (Domain) dans l'arbre d'analyse des flux.
Vous pouvez spécifier le type de modèle de viscosité turbulente pour un
Domaine (Domain) sélectionné sous le module
Turbulence (Turbulence) dans le panneau Propriétés (Properties). Le modèle de viscosité turbulente comporte deux modèles :
• Modèle k-epsilon standard
• Modèle de groupe de renormalisation (RNG)
Vous pouvez sélectionner le modèle
RNG et les
constantes associées pour un
Volume (Volume) sélectionné sous le module
Turbulence (Turbulence) dans le panneau Propriétés (Properties). Le modèle
RNG peut se révéler plus précis que le modèle
k-epsilon standard pour les flux avec stagnation et séparation. Les deux constantes supplémentaires ci-après sont codées en dur pour le modèle
RNG : η
0=4.38 et β=1.92.
Turb. Viscosity Relaxation
La constante
Turb. Viscosity Relaxation du module
Turbulence (Turbulence) contrôle le degré de correction appliqué lors de chaque itération en utilisant la formule ci-après pour la
viscosité turbulente. Vous pouvez définir la constante
Turb. Viscosity Relaxation pour un
Domaine (Domain) sélectionné sous le module
Turbulence (Turbulence) dans le panneau Propriétés (Properties).
La valeur par défaut 0 de l'option Turb. Viscosity Relaxation est la moins restrictive et autorise l'application complète de la correction. La valeur Turb. Viscosity Relaxation est comprise entre 0 et 1. L'utilisation de la valeur 0 est recommandée s'il n'existe aucun problème lié à la convergence. La définition de valeurs supérieures (>0) est préconisée en cas de besoin afin d'éviter qu'une solution ne diverge. La définition de l'option Turb. Viscosity Relaxation sur la valeur 1 constitue l'approche la plus restrictive et n'autorise aucune correction de la solution entre deux itérations.