Analyse rhéologique dans Creo > Prétraitement > Définition de la physique > Turbulence > Physique > Modèles de turbulence
  
Modèles de turbulence
Vous pouvez calculer la viscosité turbulente effective d'un circuit de fluides en vous basant sur le modèle de viscosité turbulente. Le modèle de viscosité turbulente comporte deux modèles :
• Modèle k-epsilon standard
Le modèle K-Epsilon standard est un modèle Turbulence (Turbulence) disponible dans Creo Flow Analysis.
La formulation de l'énergie cinétique turbulente k est la suivante :
La formulation du taux de dissipation turbulente ε est la suivante :
où,
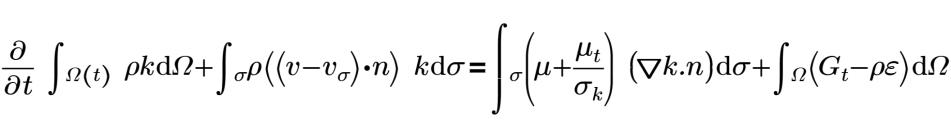
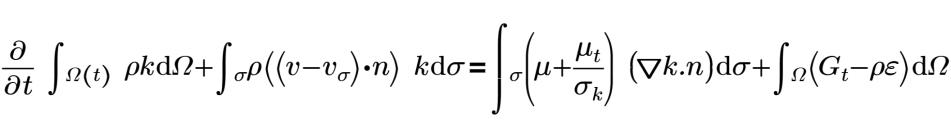
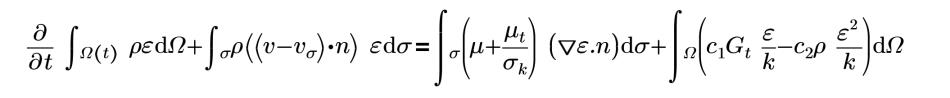
c1=1.44
constantes C1
c2=1.92
constantes C2
σk=1
nombre de Prandtl d'énergie cinétique de turbulence
σz=1
nombre de Prandtl du taux de dissipation de turbulence
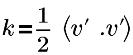énergie cinétique turbulente
v'
vitesse de fluctuation turbulente
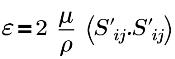taux de dissipation d'énergie turbulente
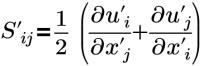tenseur des déformations
u'i(i=1,2,3)
composantes de la vitesse de fluctuation turbulente
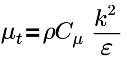viscosité turbulente, avec Cμ=0.09 et E=9.793
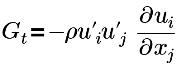terme de génération de turbulence
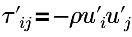tension de Reynolds
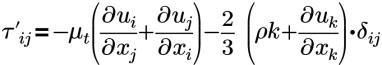approximation de Boussinesq de la tension de Reynolds
Références : Launder, B.E. & Spalding, D.B. (1974) "The numerical computation of turbulent flows", Computer Methods, Applied Mechanics and Engineering, vol. 3, pp.  269-289
• Modèle k-epsilon du groupe de renormalisation (RNG)
Le modèle k-epsilon du groupe de renormalisation (RNG) est un modèle Turbulence (Turbulence) disponible dans Creo Flow Analysis. Ce modèle est similaire au modèle k-epsilon standard, mais avec une expression impliquant deux nouvelles constantes utilisées pour modifier le terme RNG C2 dans l'équation ci-dessous :
où,
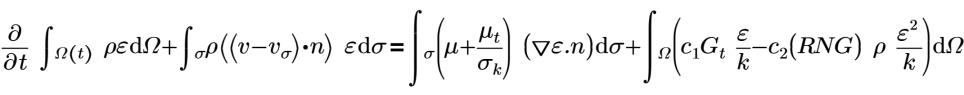
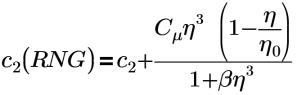
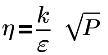
η0=4.38
constante RNG (constante codée en dur dans Creo Flow Analysis)
β=1.92
constante RNG (constante codée en dur dans Creo Flow Analysis)
P
pression locale
c1=1.44
constantes C1
c2=1.92
constantes C2
σk=1
nombre de Prandtl d'énergie cinétique de turbulence
σz=1
nombre de Prandtl du taux de dissipation de turbulence
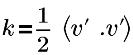énergie cinétique turbulente
v'
vitesse de fluctuation turbulente
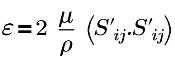taux de dissipation d'énergie turbulente
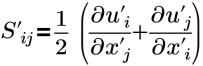tenseur des déformations
u'i(i=1,2,3)
composantes de la vitesse de fluctuation turbulente
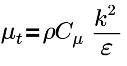viscosité turbulente, avec Cμ=0.09
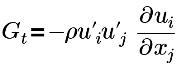terme de génération de turbulence
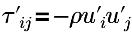tension de Reynolds
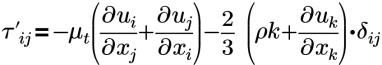approximation de Boussinesq de la tension de Reynolds
Références : Yakhot, V., Orszag, S.A., Thangam, S., Gatski, T.B. & Speziale, C.G. (1992), "Development of turbulence models for shear flows by a double expansion technique", Phys. of Fluids A, Vol. 4, No. 7, pp1510-1520