Considérations spéciales du modèle de volume de fluide (VOF)
Modèle VOF et modèle de mélange
Dans le cadre de l'approche de modélisation multiphasique eulérienne homogène, les modèles eulériens VOF et de mélange résolvent tous deux le même ensemble d'équations principales (moyennées) de mélange. Toutefois, ces modèles reposent sur des mécanismes physiques distincts et s'appliquent à des régimes d'écoulements multiphasiques différents :
• Modèle de mélange : conçu pour au moins deux phases (fluides ou particulaires), qui sont traitées comme des continuums interpénétrants. Il résout l'équation d'énergie cinétique et les équations d'énergie du mélange, mais n'assure pas le suivi de l'interface entre les phases ou n'observe aucune interface claire. Le modèle de mélange s'applique aux écoulements chargés de particules à faible débit, aux écoulements à bulles et à gouttelettes, à la sédimentation, ainsi qu'aux séparateurs cyclones. Vous pouvez également utiliser le modèle de mélange avec les vitesses relatives imposées pour les phases dispersées afin de modéliser des écoulements multiphasiques non homogènes.
• Modèle VOF : généralement une technique de suivi de surface en régime transitoire conçue pour au moins deux fluides immiscibles dans le cadre de laquelle la position de l'interface entre les phases présente de l'intérêt. Dans le modèle VOF, un seul ensemble d'équations d'énergie cinétique et d'énergie du mélange est partagé par la totalité des phases et est résolu de manière implicite. Les fractions volumiques de phase sont obtenues à l'aide d'algorithmes temporels explicites ou implicites précis utilisés avec des schémas d'advection d'ordre supérieur pour résoudre les interfaces marquées entre deux phases. Les applications types du modèle VOF comprennent les écoulements stratifiés, les écoulements à surface libre, le remplissage, le ballottement, le mouvement de bulles volumineuses dans un liquide, le mouvement du liquide après une rupture de barrage, la prédiction de fragmentation du jet (tension superficielle), ainsi que le suivi d'interfaces liquide-gaz.
La formulation VOF repose sur le fait que plusieurs fluides (ou phases) ne s'interpénètrent pas. Les fractions volumiques de phase locales permettent ainsi à elles seules de déterminer si une cellule du volume de contrôle donnée ne contient que l'une des phases ou un mélange des phases. Par exemple, si la fraction volumique de la nième phase q dans une cellule est désignée par αq, seules les trois conditions ci-après sont possibles :
◦ αq = 0 : la cellule ne contient pas la nième phase q.
◦ αq = 1 : la cellule est remplie avec la nième phase q.
◦ 0 < αq < 1 : la cellule contient l'interface entre la nième phase q et une ou plusieurs autres phases.
Par conséquent, vous pouvez procéder au suivi des interfaces entre les phases à partir de la solution d'une équation de transport pour la fraction volumique d'une ou de plusieurs phases.
Effet de la tension superficielle
La tension superficielle est la tendance élastique de la surface d'un liquide qui réduit au minimum cette surface. Prenez une bulle d'air dans un liquide. A l'intérieur de la bulle, la force nette qui s'exerce sur une molécule à cause de ses voisines est nulle. Aux interfaces liquide-air, la tension superficielle résulte du fait que les molécules liquides sont davantage attirées les unes par les autres sous l'effet de la cohésion que par les molécules de l'air par un phénomène d'adhésion. L'effet net est une force dirigée radialement vers l'intérieur à sa surface, entraînant ainsi la contraction de la bulle. La pression à l'intérieur de la bulle augmente alors afin de contrebalancer la force d'attraction intermoléculaire.
• Modèle CFS (Continuum Surface Force)
Dans
Creo Flow Analysis, le modèle VOF peut inclure les effets de tension superficielle le long de l'interface entre chaque paire de phases. Le modèle de tension superficielle adopté repose sur le modèle CFS (Continuum Surface Force) élaboré par Brackbill et autres. Cette approche considère l'effet de tension superficielle comme une force volumétrique supplémentaire concentrée à l'interface, plutôt que comme une force surfacique. Dans le cas de l'interface de surface libre illustrée
figure 2.26, le fluide primaire est la phase q (phase liquide), tandis que le fluide secondaire correspond à la phase p (phase gazeuse généralement). Conformément au modèle CFS, la courbure de surface est calculée à partir des gradients locaux dans la normale à la surface à l'interface. Supposons que
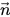
soit le vecteur normal à la surface, défini en tant que gradient de la fraction volumique du fluide primaire, α
q :
La courbure d'interface k est définie en termes de divergence du vecteur normal unitaire :
équation 2.93
où
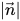
est l'intensité du vecteur
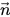
.
La force de tension superficielle à la surface est exprimée sous la forme d'une force volumétrique à l'aide du théorème de divergence, qui constitue un terme source supplémentaire ajouté à l'équation d'énergie cinétique du mélange :
équation 2.94
où σ
qp est le coefficient de tension superficielle entre le fluide q et le fluide p. Il est exprimé en N/m. L'
équation 2.94 autorise une superposition harmonieuse des forces à proximité des cellules dans lesquelles plus de deux phases sont présentes. Si une cellule ne comporte que deux phases, vous obtenez les relations suivantes :
équation 2.95
où ρ est la densité du mélange. L'
équation 2.94 est alors réduite à l'
équation 2.96
• Inclusion de la force de tension superficielle
L'importance des effets de tension superficielle est déterminée par deux paramètres sans dimension : le nombre de Reynolds Re et le nombre capillaire Ca ou le nombre de Reynolds et le nombre de Weber We :
Si Re << 1, le paramètre qui présente de l'intérêt est le nombre capillaire :
équation 2.97
où U∞ correspond à la vitesse d'écoulement libre. Les effets de tension superficielle sont ignorés si Ca >> 1, car la force de tension superficielle est trop faible.
Si Re >> 1, le paramètre intéressant est le nombre de Weber :
équation 2.98
où L est la longueur caractéristique. Les effets de tension superficielle peuvent également être ignorés si We >> 1, lorsque la force d'inertie est beaucoup plus importante que la force de tension superficielle.
Adhésion à la paroi (angle de contact)
Le modèle de volume de fluide (VOF) dispose d'une option permettant de spécifier un angle d'adhésion à la paroi en conjonction avec le modèle de tension superficielle. D'après Brackbill et autres, plutôt que d'appliquer directement cette condition aux limites à la paroi, on utilise l'angle de contact entre le fluide et la paroi à l'interface pour ajuster la normale à la surface dans les cellules à proximité de la paroi. Cette condition aux limites dite dynamique entraîne l'ajustement de la courbure de la surface près de la paroi.
Si θ désigne l'angle de contact de l'interface de surface libre au niveau de la paroi, comme indiqué
figure 2.26, le vecteur normal unitaire au niveau de la cellule à proximité de la paroi est calculé comme suit :
équation 2.99
où,
| Vecteur unitaire normal à la paroi |
| Vecteur unitaire tangentiel à la paroi |
La vitesse normale unitaire calculée
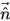
permet de déterminer la courbure locale de la surface,
équation 2.93, et par la suite la force de tension superficielle,
équation 2.94 ou
équation 2.95.
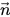 soit le vecteur normal à la surface, défini en tant que gradient de la fraction volumique du fluide primaire, αq :
soit le vecteur normal à la surface, défini en tant que gradient de la fraction volumique du fluide primaire, αq :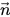 soit le vecteur normal à la surface, défini en tant que gradient de la fraction volumique du fluide primaire, αq :
soit le vecteur normal à la surface, défini en tant que gradient de la fraction volumique du fluide primaire, αq :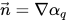

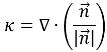
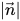 est l'intensité du vecteur
est l'intensité du vecteur 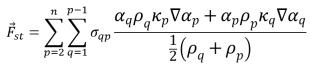

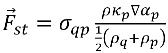
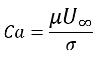
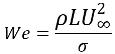
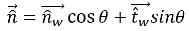
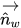
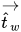
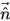 permet de déterminer la courbure locale de la surface,
permet de déterminer la courbure locale de la surface,