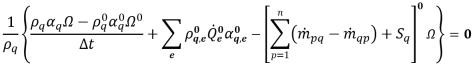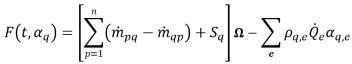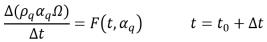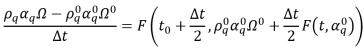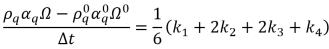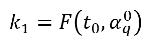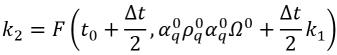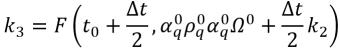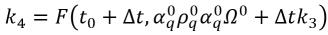數值考量
在均相多相模型中,如果不考慮速度滑動,則求解混合物動量方程式與面體積通量公式時無需進行特殊處理。這是因為它們與控制可變密度單相流的那些方程式相同。本主題著重建構壓力修正方程式,及處理相體積分數方程式,最重要的是 VOF 模型的界面求解法。
體積連續性方程式
為了滿足連續性條件約束並確保數值穩定性,會以總體積連續性而非質量連續性為基礎來建構壓力修正方程式。當您將第 q 相連續性/體積分數
方程式 2.57 除以相參照密度 ρ
rq,並將所有相組合在一起之後,會得出一個滿足質量守恆定律的總體積連續性方程式:
方程式 2.135
其中的相參照密度通常設定為相密度,即 ρrq = ρq
引入 Ω 作為計算單元的體積,並在控制體積內對
方程式 2.135 進行積分計算後,會產生離散化代數方程式:
方程式 2.136
如果您使用的方法與在單相壓力型求解器中使用的方法 (如「數值」中所述) 相同,並假設:
方程式 2.137
方程式 2.138
您可以將
方程式 2.136 重新排列為下列修正方程式:
方程式 2.139
此處的 * 和 ' 分別表示舊值與修正。
下面這個方法與單相壓力型求解器中的方法相同,其應用了 SIMPLE 類型的演算法 (Simple、SimpleC 與 SimpleS) 來關聯速度與壓力修正,並取得多相流的壓力修正方程式:
方程式 2.140
其中,
相體積分數方程式
相體積分數的傳輸由相質量守恆控制。由於在產生壓力修正方程式時應用了總體積守恆,因此求解來得出相體積分數的實際方程式也使用體積守恆的方式,以保持數值一致性:
方程式 2.141
通常,對於 n 相系統而言,只會求解 (n-1) 方程式,而第 n 相使用物理限制取得:
方程式 2.142
如果遵循離散化方法,
方程式 2.141 的積分形式如下所示:
方程式 2.143
如動量、能量及總體積守恆方程式中所證,空間與時間離散化法對於數值精確性而言至關重要。對於體積分數方程式,除標準隱式時間法以外,常見的方法是將顯式時間推進與高解析平流法搭配使用,如此您可以更精確地捕捉 VOF 模型中的界面。接下來的內容將詳細說明隱式與顯式 VOF 公式。
• VOF 隱式公式
若使用 VOF 隱式公式,離散化相體積分數方程式的一般式如下:
方程式 2.144
在此方程式中,目前時間步長的相體積分數 α
q 為目前時間步長的量。因此,作為動量、能量與壓力修正方程式,離散化體積分數
方程式 2.144 會在每個時間步長迭代求解。在
Creo Flow Analysis 中,所採用的隱式公式概括如下:
◦ 平流配置 - 體積通量
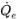
將根據目前時間步長的流動欄位進行計算。在單元中心值 α
q,P、
q,E 與相鄰單元 P 與 E 的梯度 (
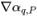
、
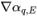
) 的各項中,可以求出面值 α
q,e 的近似值。正如在被動純量方程式中,平流法的一般式如下:
方程式 2.145
如果針對參數 γ、βP 與 βE 使用不同值,並使用用來計算體積分數梯度的方案,可以針對體積分數方程式開發出四種平流法:「一階上風法」(First-Order Upwind)、「二階上風法」(Second-Order Upwind)、「中心差分法」(Centre Difference) 以及「高解析法」(High Resolution)。
方程式 2.146
沒有上標的變數是指目前時間步長的值。有上標 0 或 00 的變數是指之前時間步長的值。
參數 β 和 βCN 在 0 到 1 之間變化,可用於確定時間法。具體而言,針對相體積分數方程式的離散化採用來三種時間法:
▪ 尤拉一階上風法 (Euler First-Order Upwind):β = 0,βCN = 1
▪ 三級二階法 (Three-Level Second-Order):β = 0,βCN = 1
▪ 克蘭克-尼科爾法 (Crank-Nicolson Method):β = 0,βCN = 0.6 (預設)
• VOF 顯式公式
當使用顯式公式來求解 VOF 方程式時,會根據之前時間步長的已知量直接計算目前時間步長的相體積分數。因此,VOF 顯式公式不需要每個時間步長期間的
方程式 2.144 的迭代解。不過,由於其餘的傳輸方程式均採取隱式求解方式,因此用於體積分數計算的時間步長通常會比用於其他傳輸方程式的時間步長小。對於顯式 VOF 公式,需要確定子時間步長,此值可以自動計算,也可在
Creo Flow Analysis 中提供。
在使用顯式公式的情況下,離散化相體積分數方程式的公式如下:
方程式 2.147
其中的平流項與源項皆為根據之前時間步長的已知量所計算。體積通量
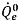
的計算方式與隱式公式中
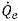
的計算方式相同。面體積分數
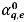
也可使用四種平流法之一進行估計:「一階上風法」、「二階上風法」、「中心差分法」以及「高解析法」。
Creo Flow Analysis 針對顯式時間推進法提供下列三種演算法:
• 尤拉 一階顯式法 (Euler First Order Explicit) - 體積分數方程式會離散化為如下:
方程式 2.148
• 龍格-庫塔 二階法 (Runge-Kutta Second-Order) - 引入了下列函數:
方程式 2.149
方程式 2.150
二階龍格-庫塔 顯式法形式如下:
方程式 2.151
• 龍格-庫塔 四階法 (Runge-Kutta Fourth-Order) - 對於相 q 體積分數方程式,四階龍格-庫塔 顯式法形式如下:
方程式 2.152
其中
方程式 2.153
方程式 2.154
方程式 2.155
方程式 2.156
對於 n 相系統,通常只會求解 (n-1) 相體積分數,剩餘的一相可從物理限制取得,
方程式 2.142。不過,您也可以求解所有 n 相體積分數方程式,可透過使用所計算總體積分數的總和調整每個相的比例,來滿足
方程式 2.142。在迭代過程中,這可能會小於或大於 1。
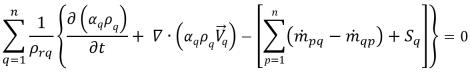
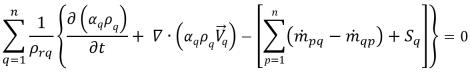
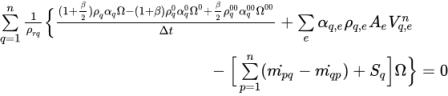
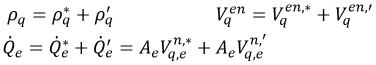
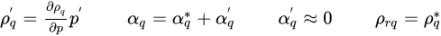
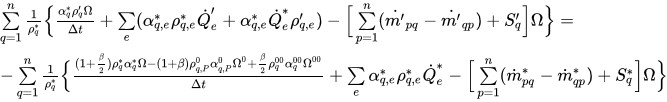
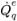
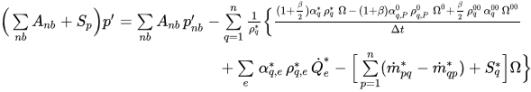
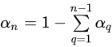
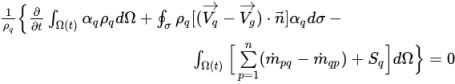
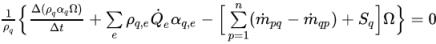
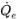 將根據目前時間步長的流動欄位進行計算。在單元中心值 αq,P、q,E 與相鄰單元 P 與 E 的梯度 (
將根據目前時間步長的流動欄位進行計算。在單元中心值 αq,P、q,E 與相鄰單元 P 與 E 的梯度 (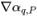 、
、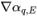 ) 的各項中,可以求出面值 αq,e 的近似值。正如在被動純量方程式中,平流法的一般式如下:
) 的各項中,可以求出面值 αq,e 的近似值。正如在被動純量方程式中,平流法的一般式如下: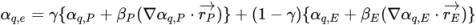
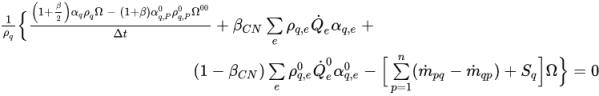
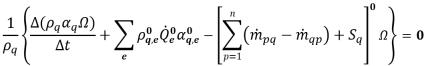
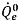 的計算方式與隱式公式中
的計算方式與隱式公式中 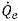 的計算方式相同。面體積分數
的計算方式相同。面體積分數 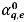 也可使用四種平流法之一進行估計:「一階上風法」、「二階上風法」、「中心差分法」以及「高解析法」。
也可使用四種平流法之一進行估計:「一階上風法」、「二階上風法」、「中心差分法」以及「高解析法」。