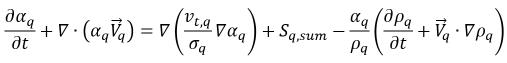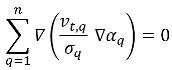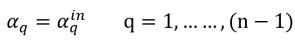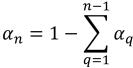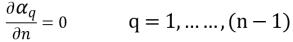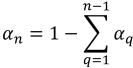尤拉模型與統御方程式
本節說明流體體積 (VOF) 與混合多相模型的統御方程式,以及為多相流中的亂流與邊界建模。
一般多相統御方程式
在尤拉-尤拉 方法中,會將多相系統中的不同相或成分假設為共用相同流壓力的數學意義上的互穿連續體。由於物理空間或體積由所有相共用,因此引入了相體積分數的概念來描述相傳輸。假設相體積分數為空間與時間的連續函數,且其總和等於一。會針對每個相應用守恆定律,以導出一組統御方程式,其由理論或經驗組成關係結束。尤拉-尤拉 方法常用的模型有兩種類型:
• 非均相或尤拉 多流體模型 - 直接對包括動量、能量、亂流、物種相在內的每個相求解統御方程式,及體積分數方程式。相與相之間的交互作用,動量、質量、物種與熱之間的相間傳送使用物理子模型建模。
針對第 q 相使用一般相純量 ϕq, q 後,相 q 的廣義方程式形式如下:
方程式 2.54
其中,
ρq | q 密度 |
| 速度 |
Sϕq | 源項 |
Tϕq | 擴散係數 |
αq | 第 q 相中的體積分數 |
ϕq 表示多相系統中的應變數:
方程式 2.55
其中,
Uq、Vq、Wq | 相速度分量 |
Hq | 相總焓 |
Yqi | 第 q 相中物種 "i" 的質量分數 |
k | 亂流動能 |
ε | k-ε 模型的亂流動能消散率 |
p | 第 p 相 |
n | 多相系統中的相數 |
| 從第 q 相到第 p 相的質量傳遞 |
θpq | 包括動量、能量及物種在內之傳輸量的直接相交換 |
透過針對相間物種、質量、動能與熱交換使用子模型,您可從在此處為廣義的傳輸方程式導出一組完整的流統御方程式。
• 均相多相模型 - 非均相模型的簡化版經濟型替代模型。均相建模方法會計算流、能量及亂流的相統御方程式的平均值,以得出一組混合物傳輸方程式,同時仍會求解相體積分數。對於混合物純量 ϕm,廣義統御方程式的運算式如下:
方程式 2.56
其中,
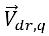
是相 q 的速度與混合物速度之間的差:
均相多相模型是相間傳送率較大的尤拉-尤拉多相流的一種限制情況。基本假設是所有相共用相同的壓力場。在此假設的基礎上,均相模型會藉由假設所有相共用共同的速度、溫度與亂流場,進一步導致簡化完整非均相尤拉 多流體模型。此方法是完整尤拉 多流體模型的一種很好的替代方法,因為它的計算程序簡單,運算方面也很經濟實惠。實際上,在例如自由表面流 (VOF)、空蝕或其他高度混合物多相流的情況下,不僅完整多流體模型可以執行,均相模型也可以執行,而不需要動量與能量方程式中的相間交換模型。
在 Creo Flow Analysis 中,目前的多相模型僅採用均相建模方法。注意力集中在建模自由表面流 (流體模型體積) 與均相液氣二相流 (混合模型)。原則上,您可以針對 n 相流應用建模功能。
VOF 與混合多相模型
流體體積 (VOF) 與混合多相模型使用均相建模方法。每一相體積分數的傳輸方程式皆從
方程式 2.54 取得。混合物動量與能量的統御方程式則使用
方程式 2.56 和質量、動量與能量守恆定律得出。接下來將介紹一組統御方程式。
• 相 q 體積分數方程式
方程式 2.57
其中的
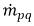
是
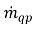
質量交換率,這兩項分別表示相 q 的源與匯的大小。在相間質量傳遞過程中,其中一項通常為零。請參閱如下範例:
在蒸發過程中,液相 q 會損失質量,
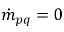
且
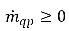
,而在汽相中,則為
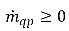
且
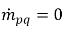
。
對於 n 相系統,相體積分數的總和滿足物理限制:
方程式 2.58
或總質量守恆:
方程式 2.59
其中混合物量定義如下:
◦ 體積平均混合物密度
方程式 2.60
◦ 質量平均混合物速度
方程式 2.61
• 混合動量方程式 - 透過將系統中所有相的個別動量方程式相加取得。從
方程式 2.56 中,設定
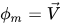
之後,您將得到
方程式 2.62
其中的混合物量定義如下:
◦ 體積平均混合物黏度:
方程式 2.63
方程式 2.62 中的擴散係數 Γ 使用混合物動力黏度 μ 與亂流黏度 μ
t 計算得來。右邊的最後兩項表示直接動量傳送以及質量傳遞引發的動量交換。它們由相漂移速度
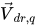
決定,定義如下:
方程式 2.69
在均相方法中,您可以使用代數模型建模此漂移速度。不過,在目前的 VOF 與混合模型中,假設相之間沒有滑動:
因此,兩個動量交換項均為零。
◦ 混合物能量方程式
在沒有速度滑動的情況下,混合物的能量方程式採用下列形式:
方程式 2.70
其中的混合物變數定義如下:
▪ 體積平均熱導係數
方程式 2.71
▪ 質量平均混合物能量與焓
方程式 2.72
在混合物能量
方程式 2.70 中,黏性加熱項
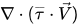
是當成在單相流中計算所得;S
E 是總外熱源或使用者熱源。
右側的最後一項是因質量傳遞所導致的界面熱傳遞。假設相共用相同溫度的情況下,Lgp 這一項取決於求解能量方程式中 Hq 與 Hp 的定義。
如
熱模組所述,材料的靜焓由兩部份組成:標準狀態參考焓與可感熱焓。如果您假設相 q 為液體,且相 p 為蒸汽,則相總靜態焓如下所示:
方程式 2.73
方程式 2.74
其中,
pref | 參照壓力 |
Tref | 參照溫度 |
hq,ref | 相 q 標準狀態參照焓 |
hp,ref | 相 p 標準狀態參照焓 |
參照焓的差為
方程式 2.75
是在參考溫度 Tref 與壓力 pref 下的潛熱。
▪ 包括標準參考焓:
方程式 2.76
方程式 2.77
由於相形成焓或潛熱而導致產生的差 Lpq 已包括在能量方程式中。數量將設定為零:
Lpq=0
此外,由於質量傳遞而導致的熱傳遞,
方程式 2.70 中的最右側一項在混合物能量方程式中為零。
▪ 排除標準參考焓:
在 CFD 求解器中,不會直接求解總焓。相反,僅相對於飽和溫度的可感熱焓會包括在求解的焓與內部能量中:
方程式 2.79
方程式 2.80
那麼,Lpq 不為零。它應該是潛熱:
方程式 2.81
其中,
方程式 2.82
方程式 2.83
在 Creo Flow Analysis 中,依預設會自動視為標準狀態參照焓。不需要使用者輸入。
亂流模型
• 混合物 k-ε 亂流模型
在流體體積 (VOF) 與混合多相模型中,會透過單相亂流模型的延伸,來說明亂流對相混合的影響。在
Creo Flow Analysis 中,
亂流模組所述的亂流模型與壁附近的處理會延伸至多相流。如果提供混合流的量,標準和 RNG k-ε 模型擁有與單相亂流中一樣的一般式:
方程式 2.84
方程式 2.85
其中的混合物密度 ρ、速度
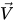
以及分子黏性 μ 分別使用
方程式 2.60、
方程式 2.61 與
方程式 2.63 中的關係,從對應的相值計算得來;S
k 與 S
ε 包括可能的外源與使用者源以及相交互作用源。混合物的亂流黏度 μ
t 直接從下列運算式計算得來:
方程式 2.86
亂流動能的結果是根據混合物亂流黏度與速度梯度計算所得:
方程式 2.87
其中 S 是應變平均混合率的模數,
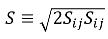
相 q 的亂流黏度可以計算為:
方程式 2.87
• 亂流擴散效應
針對多相亂流流動,當計算瞬間界面拖曳項目的平均值時,會產生亂流擴散力,其表現與相擴散類似。非均相
尤拉 多流體模型通常會將此亂流效應視為其他相間力,取決於相動量方程式中相體積分數的梯度。但是,也可以透過直接將此亂流效應視為相體積分數方程式中的亂流擴散項來進行建模。透過分割
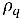
和分組所有來源
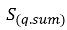
(相間質量傳輸與外部質量來源的總和),您可在亂流中取得相 q 體積分數的下列統御方程式:
其中相 q 中右側第一項為亂流擴散項,它必須符合下列條件約束以便滿足總質量守恆:
亂流擴散項通常作為一個選項實行。依預設,此項不包含在內。
多相邊界的建模
在流體體積 (VOF) 與混合多相模型中,流動與能量方程式中的邊界條件與單一相流動的邊界條件相同。這些將在
流動與熱模組中介紹。對於相體積分數,在下列情況下,只會應用固定值與零梯度:
• n 相入口邊界
針對 (n-1) 個相,入口體積分數已預先確定,而第 n個相使用物理限制取得:
方程式 2.88
方程式 2.89
並且每個相上的體積分數必須為非負數。
• 出口/對稱/壁邊界
對於 (n-1) 相,會針對所有出口、對稱及壁邊界應用零梯度條件,而第 n相使用物理限制取得:
方程式 2.90
方程式 2.91
上述統御方程式、亂流模型以及邊界條件形成了均相 VOF 與混合多相模型的基礎。如果沒有外源項或使用者源項以及相間質量傳遞,它們是一個封閉的方程式系統,而且可以使用以壓力為基礎的有限體積多相求解器以數值方式求解。在許多實際應用中,若要精確捕捉各自的物理現象與過程,某些特定子模型 (例如 VOF 模型中的表面張力) 以及相間質量傳遞是必不可少的。不會將子模型歸併到外源或使用者源中,因此最好將它們包括在內建模型中。
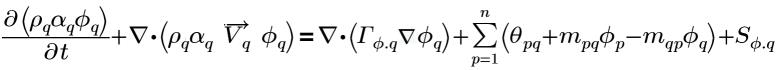
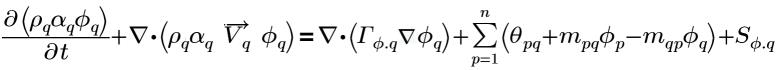
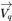
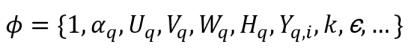
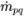
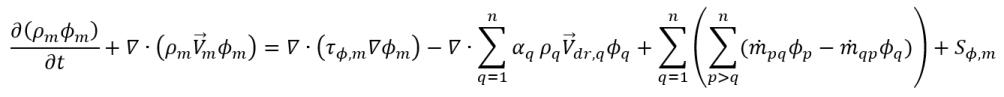
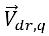 是相 q 的速度與混合物速度之間的差:
是相 q 的速度與混合物速度之間的差: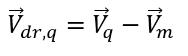
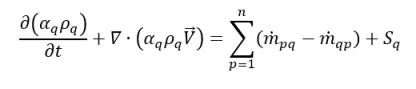
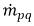 是
是 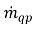 質量交換率,這兩項分別表示相 q 的源與匯的大小。在相間質量傳遞過程中,其中一項通常為零。請參閱如下範例:
質量交換率,這兩項分別表示相 q 的源與匯的大小。在相間質量傳遞過程中,其中一項通常為零。請參閱如下範例: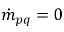 且
且 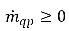 ,而在汽相中,則為
,而在汽相中,則為 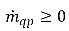 且
且 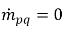 。
。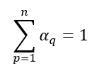
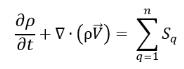
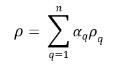
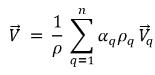
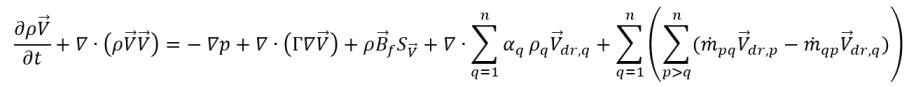


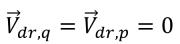
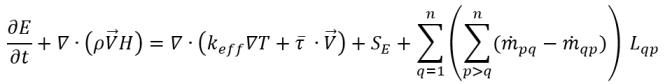
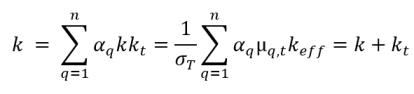
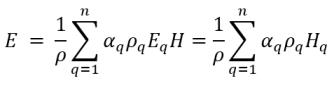
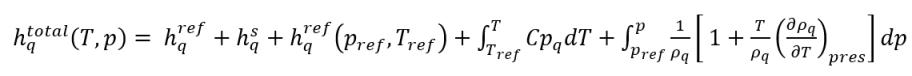
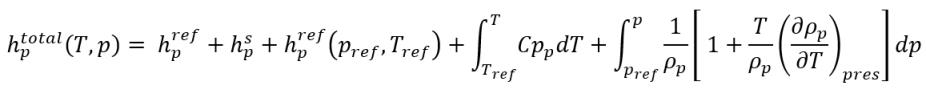
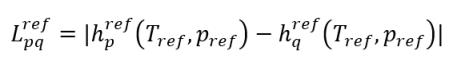
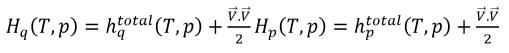
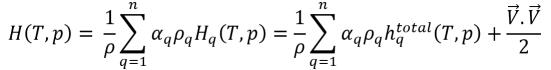
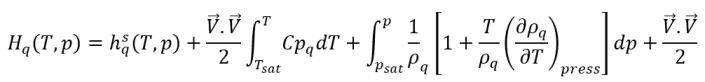
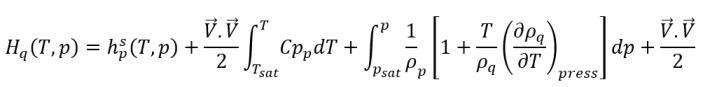
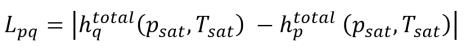
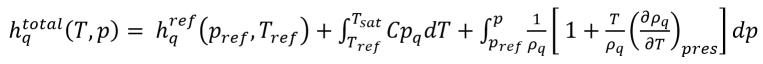
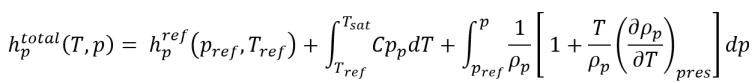
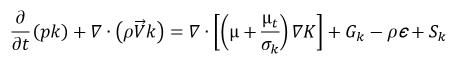
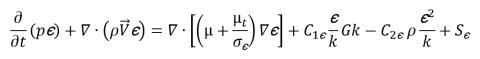
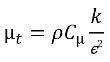
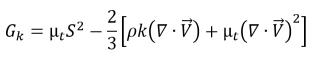
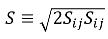
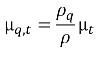
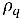 和分組所有來源
和分組所有來源 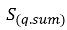 (相間質量傳輸與外部質量來源的總和),您可在亂流中取得相 q 體積分數的下列統御方程式:
(相間質量傳輸與外部質量來源的總和),您可在亂流中取得相 q 體積分數的下列統御方程式: