Voting Gate
The voting gate is used to indicate that the output occurs if and only if at least m out of n input events occurs. The input events do not need to occur at the same point in time but should be present at the same time. The output occurs when at least m input events occur. When m is 1, the voting gate behaves like an OR gate.

Summary of Logic:
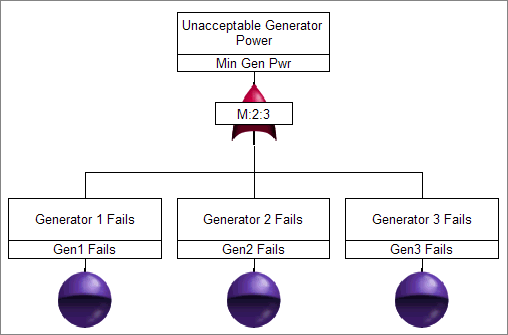
If m is 2 and n is 3, two input events must be TRUE for the output to be TRUE. If zero or one input event is TRUE, the output is FALSE.
A truth table for a 2 out of 3 voting gate follows. The Boolean equation for a three-input voting gate is T = (A * B) + (B * C) + (C * A).
A | B | C | Output |
|---|---|---|---|
T | T | T | T |
T | T | F | T |
T | F | T | T |
T | F | F | F |
F | T | T | T |
F | T | F | F |
F | F | T | F |
F | F | F | F |
Example
Power is supplied by three generators. When two generators are working, adequate power is supplied. When only one generator is working, not enough power is supplied.