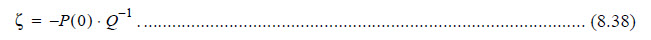Mean Time to Failure (MTTF) of a system can be obtained by integrating the system reliability R(t):

If the system reliability expression is in the following form:

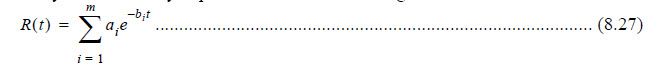
Then, MTTF of the system is:

For example, the reliability of the two-unit parallel system is:

Hence, MTTF is:

To find MTTF using equation (8.26), first, system reliability must be computed as already shown. In general, computing R(t) is difficult. However, this section provides an easy method for computing MTTF.

To calculate MTTF, it is necessary to classify the states. This section presents only the details that are required to analyse the MTTF and other commonly used reliability characteristics. A Markov process is called an Ergodic Markov process if it is homogeneous (time-independent) and the final value of the probability (probability at infinity) of a state is independent of the initial state.

This is possible only when there are no absorbing states. In reliability analysis, this means that system is repairable. Therefore, a non-trivial (non-zero) solution for system steady-state availability is possible only when there are no absorbing states in the system (the system is repairable). However, if the system is non-repairable (at least for some type of failures), then there exist absorbing as well as non-absorbing (transient) states. Further, as in case of reliability analysis, we should consider all failed states as absorbing states to compute system MTTF.

Consider that there are r absorbing states (failed states) in the system and (n-r) non-absorbing (transient) states in the system. For example, consider the system in Figure 8-3. The corresponding matrices, T and Q=BT are as follows:

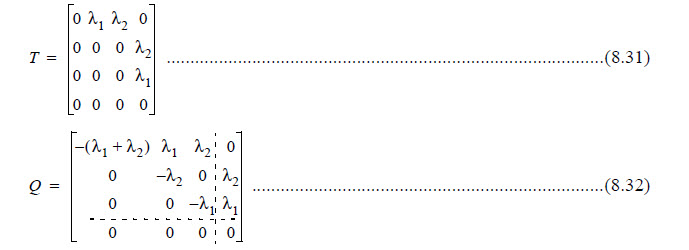
For this example, state 4 is absorbing state; hence, r=1. It should be noted that all elements in a row of Q that correspond to an absorbing state are 0s. We can partition matrix Q. (Although this partition is not necessary to compute MTTF, it is helpful for finding other system characteristics.)

Where:

QT=The square matrix of size n-r. It is called the truncated transition matrix associated with T.

For this example:

Find the matrix M, which is the inverse of -Qt:

It should be noted that the element mij of the matrix represents the amount of time spent in state before reaching an absorbing state when the system is initially in state I. Therefore, when the system is initially in state 1, the sum of all the elements of row 1 is the MTTF of the system.

Therefore, for this system:

It should be noted that if MTTF is finite (if there are some absorbing states), then MTTF can also be found directly using —Q-1 (if —Q-1 exists). Further, if the initial state probability is specified (if there are multiple initial states), then MTTF is the sum of all elements of the vector ζ: