Importance Measure Usage
The previous paragraphs have shown how to calculate the three importance measures (Birnbaum, Criticality and Fussell-Vesely). Also, they have shown how to use each importance measure by rank ordering the basic events by the values of the importance measures and then considering improving first that basic event with the highest importance measure value.
If all three importance measures yield the same rank ordering of basic events, then the strategy for using the importance measures is straightforward. However, when the three importance measures yield different rank orderings of basic events, the following guidelines suggest how to select an appropriate solution:
• Keep in mind that the goal is to assist in selecting the next basic event to consider for improvement. It cannot be concluded definitively that a particular basic event must receive the next improvement effort.
• Ensure the correct primary time point is chosen. The rank ordering of the importance measures may be different at different time points.
• Consider averaging the three-way ranking of the three importance measure rank orderings for each basic event. This may indicate a consensus of the three measures. (An example follows.)
• Study the sequential ranking, first by ranking by the Fussell-Vesely or Criticality importance measure and then break ties within the ranking by the Birnbaum importance measure.
• When in doubt or when calculation performance is an issue, the Criticality importance measure is probably a reasonable single measure to use. It considers the probability of the basic event (an improvement over the Birnbaum importance measure). However, if this is a problem with uninformative results caused by AND gates (as can happen with the Fussell-Vesely importance measure), then use the Birnbaum importance measure.
Example
A possible procedure for determining the average rank order when the three importance measures assign different orderings to the basic events follows. Refer to Appendix C for detailed application information.
1. For each of the three importance measures, assign the rank ordering number to each basic event.
2. For each basic event, average these three rankings.
3. Rank these averages to get an overall ranking for each basic event. The example in Importance Measure Usage yields the following values for the three importance measures.
|
Event
|
Birnbaum
|
Criticality
|
Fussell-Vesely
|
|---|---|---|---|
|
A1
|
0.7407952
|
0.7408114
|
1.0000000
|
|
A2
|
0.7407952
|
0.7408114
|
1.0000000
|
|
A3
|
0.0000743
|
0.0000071
|
0.1903293
|
|
B1
|
0.0000141
|
0.0000141
|
0.1903293
|
|
B2
|
0.0000743
|
0.0000071
|
0.1042212
|
|
B3
|
0.0000743
|
0.0000071
|
0.1042212
|
4. Create a rank ordering by assigning the number of the ranking to the basic event.
|
|
If two or more basic events are tied (i.e., they have the same importance measure values), then assign each one of them the average of the rankings that they would have received if these ties had been ignored. This yields the following rank orderings and their rank ordering numbers:  |
These rank ordering numbers can be rearranged by events to make it easier to tabulate. Note that the sum of the ranks of N basic events should be:
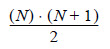
In this case, N = 6, so the sum of the ranks should be:

This serves as a check on both the arithmetic and tabulation, as shown in Table 5-14:
Event | Birnbaum | Criticality | Fussell-Vesely | Average Rank |
|---|---|---|---|---|
A1 | 5.5 | 5.5 | 5.5 | 5.5 |
A2 | 5.5 | 5.5 | 5.5 | 5.5 |
A3 | 3.0 | 2.0 | 3.5 | 2.8 |
B1 | 1.0 | 4.0 | 3.5 | 2.8 |
B2 | 3.0 | 2.0 | 1.5 | 2.2 |
B3 | 3.0 | 2.0 | 1.5 | 2.2 |
Check Sum | 21.0 | 21.0 | 21.0 | 21.0 |
Thus, the average ranking orders the effort for improvement in basic events as

Earlier, an ad hoc ordering of the basic events concluded with this ordering:
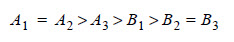
It can be seen that the mechanical average ranking ordered the basic events essentially the same as the ad hoc reasoning ordered them, and it ordered the basic events exactly as Fussell-Vesely ordered them. For additional information, refer to Application of Importance Measures.