範例:線性預測方法
使用 burg 及 yulew 函數為指定的線性預測模型產生係數。這些函數分別實行 Burg 方法與 Yule-Walker 演算法。如需這些演算法及其背後數學運算的說明,請參閱 Sophocles J. Orfanidis 的 Optimum Signal Processing (最佳信號處理),Macmillan 出版 (1989)。
Yule-Walker 預測
1. 使用 cos 函數定義餘弦信號。
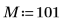
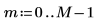
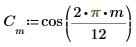
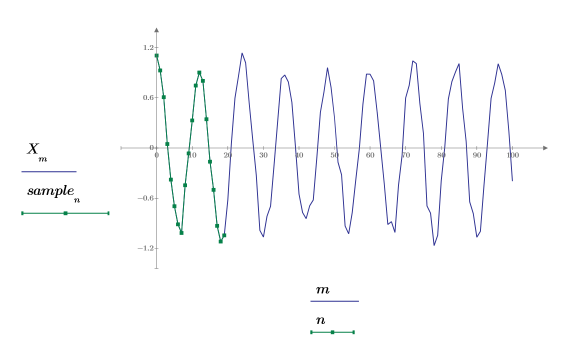
2. 繪製信號。
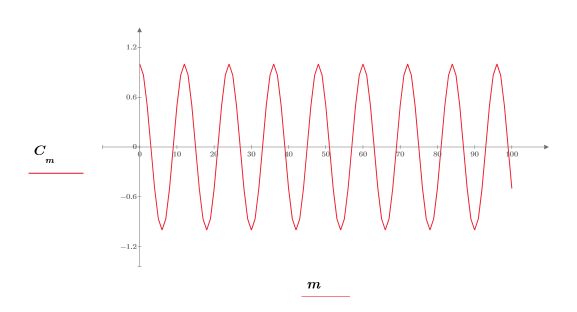
3. 使用 rnd 函數將隨機雜訊加入到信號。
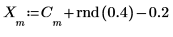
4. 繪製原始信號與雜訊信號。
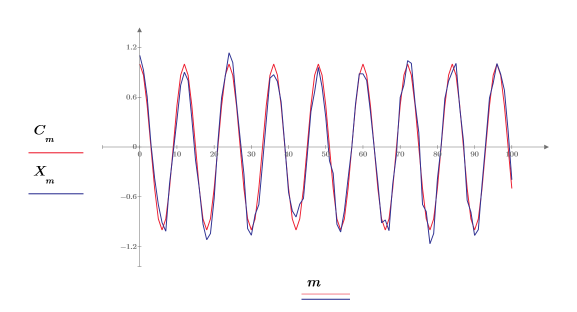
信號減去 0.2,以集中 0 振幅周圍的隨機元件。
5. 從信號的開頭擷取短的樣本集。
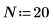
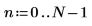
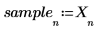
6. 設定預測順序,並使用 yulew 函數計算係數。
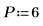
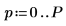

◦ 這些係數適用於近似於原始信號的全極點濾波器。一如預期,有一個大的極點代表餘弦,數個較小的極點則近似於雜訊。
◦ 順序 P 決定預測序列中下個值所用的連續值數目。使用係數向量的第一到第六個元素,忽略恆為 1 的第零個元素。當 y 用為預測誤差濾波器以產生預測誤差的全集合時,即需要此 1。
7. 比較原始數據與使用信號中舊有之 P 點計算得出的預測點。這會顯示濾波器用於信號 X 的良適性如何。
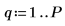
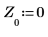
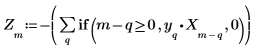
8. 繪製原始信號與預測的信號。
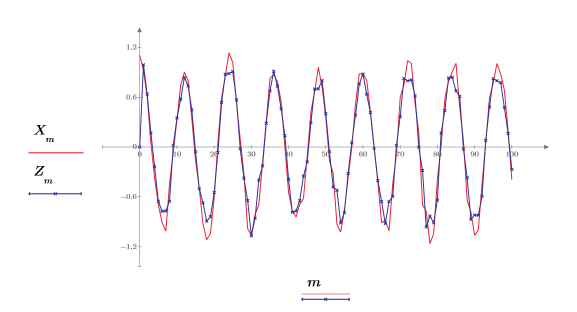
即使只使用前 20 個數據點,近似值仍非常好。
9. 使用 response 函數將係數陣列用作濾波器,再計算輸入時的樣本回應,產生 Yule-Walker 係數的預測誤差。
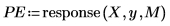
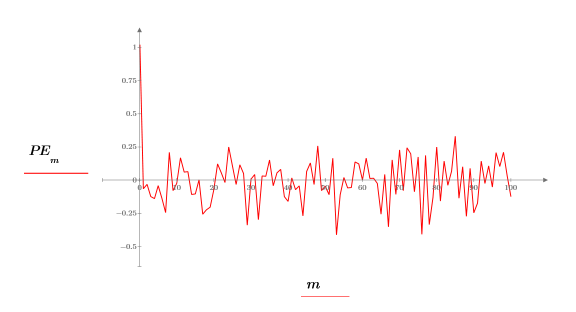
完整的係數陣列有時亦稱為預測誤差濾波器。
10. 核對這些誤差可看出前兩份繪圖的差異。
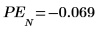
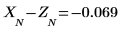
Yule-Walker 演算法會最小化預測誤差的平方和。
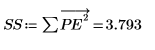
11. 干擾 y (除第一個係數之外,在所有係數中隨機加上微量) 並重新計算總和 (將游標置於 rnd 函數下,並按數次 [F5]),對最小化進行抽查。
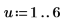
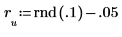
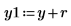
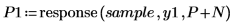
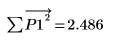
Burg 預測
1. 建構線性預測運作良好的序列:具備已知係數的自遞歸程序。
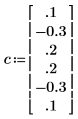
2. 初始化時間序列。
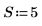
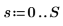
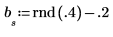
3. 使用自遞歸與雜訊產生其餘的序列。
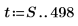
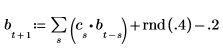
4. 將整個時間序列作為樣本,並計算 6 階的模型係數,然後使用 burg 函數計算係數。
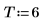
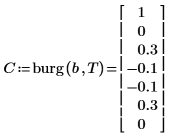
5. 使用本文件的符號慣例,比較實際產生處理程序的係數。
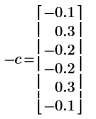
◦ 第零個係數已忽略,因為它始終等於一。
◦ C 計算的元素 1 和 5 不同。
6. 使用 Burg 係數向量 C 產生預測誤差。
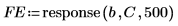
◦ Burg 方法會將 0 加權指派給第一個 P 誤差,所以最小化不受樣本補零的影響,情況與最小化由 Yule-Walker 執行一樣。
◦ Burg 條件也關係到前向誤差 FE 及後向誤差 BE。
7. 使用 response 與 reverse 函數計算後向誤差。
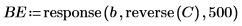
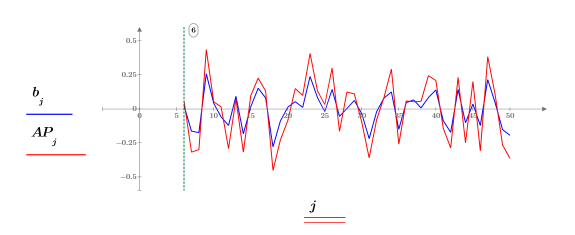
8. 使用預測誤差 FE 及自遞歸函數 b 計算實際的預測 AP,然後繪製從第 Pth 項開始的預測及實際序列片段。
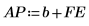
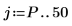
頻譜預測
您可使用線性預測模型產生的係數,計算成型程序的功率頻譜。Burg 演算法在本文中已知為最大熵值頻譜分析 (MESA),而且在某些情況下,它比 FFT 更能精確判斷短時間序列的頻譜。
預測由正弦曲線加上高斯雜訊所構成之程序的功率頻譜。
1. 使用 sin 函數定義具有兩個正弦元件的信號。
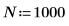
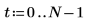
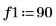
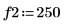
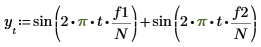
2. 使用 gaussn 函數加入若干高斯雜訊。
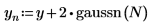
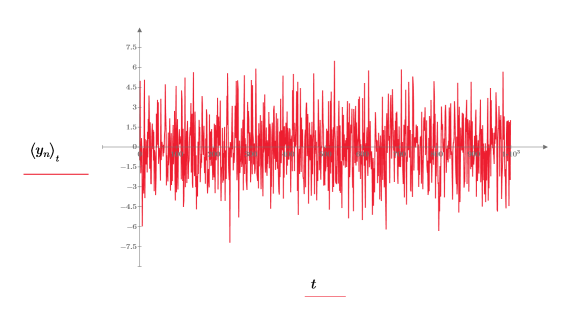
gaussn 函數跟在均數為 0 且標準差為 1 的高斯機率分佈之後,傳回亂數的 n 元素向量。
3. 定義線性預測的兩個階數。
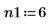
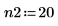
4. 使用 burg 函數計算具有兩個階數的自遞歸模型的頻譜,其中使用整個時間序列作為樣本。
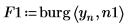
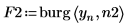
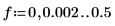
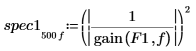
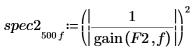
6. 繪製兩個功率頻譜。
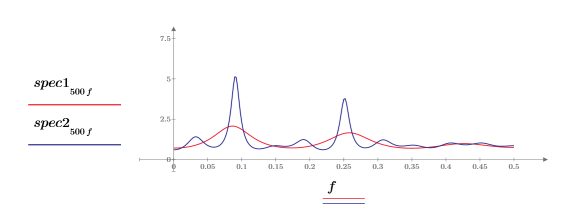
◦ 每個功率頻譜有兩個尖峰。
◦ 這兩個頻譜的較低和較高頻率尖峰發生於相同的頻率。
7. 將 spec1 與 spec2 分別再次分隔為兩個區段,以協助求解其增量尖峰與它們出現的頻率。
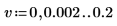 | 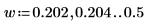 |
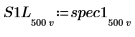 | 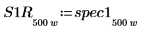 |
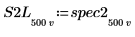 | 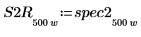 |
8. 使用 if 函數定義會傳回指定的區段具有尖峰時的頻率,然後使用該頻率求解每個頻譜繪線的左側與右側尖峰。
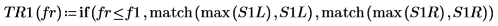 | |
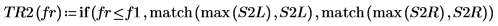 | |
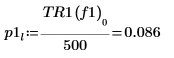 | 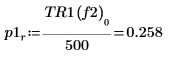 |
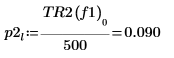 | 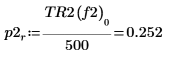 |
9. 使用 max 函數計算每個尖峰的量值。
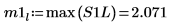 | 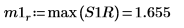 |
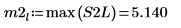 | 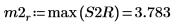 |
10. 分別繪製每個函數。使用水平與垂直標記,以顯示每個尖峰的量值及其發生時的頻率。
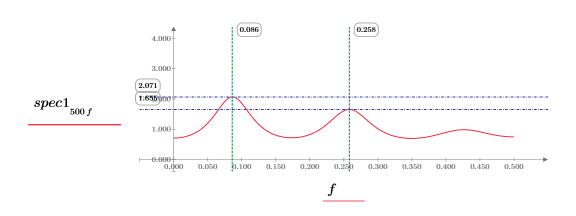
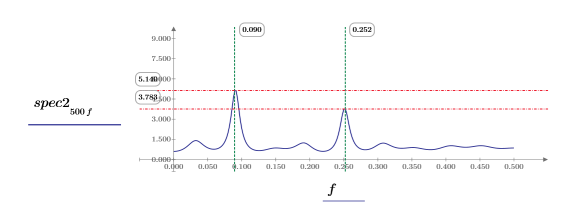
◦ 在重新計算工作表時,觀察這兩個繪圖。
◦ 尖峰的量值在每次重新計算時會有所不同,它們通常具有不同的值。但是,也可能會是相同的量值。
◦ 尖峰發生在相同的頻率。
如需有關此頻譜預測方法的詳細資訊,請參閱 Digital Spectral Analysis with Applications by S. Lawrence Marple, Jr. (Prentice-Hall, Inc)。