Символьные гамма-функции
• Psi(z) - возвращает производную натурального логарифма гамма-функции Γ(z). Дигамма-функция определяется следующим образом:
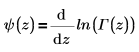
• Psi(n, z) - возвращает производную nth от Psi(z). Полигамма-функция определяется следующим образом:
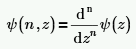
Функция Psi(z) связана с функцией Psi(n, z) следующим образом:
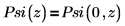
Аргументы
• z - действительный или комплексный скаляр или вектор действительных или комплексных скаляров.
• n — неотрицательное целое число.
Дополнительная информация
• Версию функции Psi с одним аргументом можно вычислять как аналитически, так и численно. При численном вычислении z также может быть комплексным скаляром или вектором комплексных скаляров.
• Можно вычислить две версии аргументов функции Psi только в символьном виде.