Разложение сингулярных значений
• svds(A) - возвращает вектор, содержащий сингулярные значения A, положительные квадратные корни из eigenvalues матрицы AH·A, где AH - результат сопряженного транспонирования матрицы A. Можно вычислить AH при помощи операторов transpose и complex conjugate следующим образом.
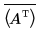
• Функция svd(A) возвращает вектор из 3 вложенных массивов.
Первый массив содержит вектор s сингулярных значений, возвращенных функцией svds. Следующие два массива - матрицы U и VH, удовлетворяющие условию A = U∙diag(s)·VH. Третьим элементом VH является сопряженное транспонирование V.
Третий массив - это VH, а не V. Это означает, что сопряженное транспонирование уже было применено к возвращенному массиву. Нет необходимости применять его снова. Можно использовать в формуле сам возвращенный массив.
Аргументы
• A — массив размером m × n, где m ≥ n. Для функции svd элементы массива должны быть вещественными числами; для функции svds допустимы комплексные значения.
Дополнительные сведения
• Сингулярные значения всегда являются вещественными положительными числами. Очень малые значения должны интерпретироваться как 0.
• Функция svd использует библиотеки Intel Basic Linear Algebra Subprograms (BLAS) и Linear Algebra Package (LAPACK).