Несходимость числовой оценки интегралов с бесконечными пределами
В этом разделе приведено решение двух случаев ошибок несходимости при числовой оценке интегралов с одним или двумя бесконечными пределами интегрирования.
Чтобы объяснить два случая, определите среднее значение μ и среднеквадратическое отклонение σ.
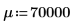
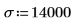
Случай I: интеграл с одним бесконечным пределом интегрирования
Задайте для переменной множителя n значение 1, а затем определите функцию g(x) в терминах встроенной функции плотности вероятности dnorm.
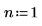
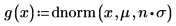
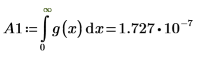
Если n=1, вычисление интеграла g(x) в диапазоне [0, ∞] не возвращает сообщение об ошибке, но возвращает очень маленькое значение.
Обходное решение для случая I
Увеличьте значение n до n=2 и повторите вычисление интеграла.
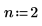
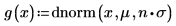
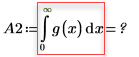
Увеличение значения n до n=2 приводит к ошибке, поскольку расчет не сходится к решению.
В качестве обходного решения задайте для переменной T значение, близкое к концу g(x), а затем разделите один интеграл на два: один - охватывающий диапазон [0, T], а второй - охватывающий диапазон [T, ∞].
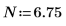 | 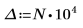 |
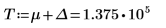 |
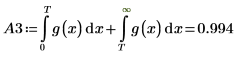
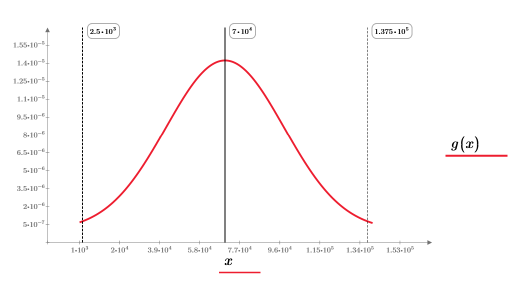
Разделенный интеграл A3 возвращает хороший ответ при n=1 или n=2. Постройте график g(x) и добавьте вертикальный маркер T, чтобы увидеть, насколько близок он к концу g(x).
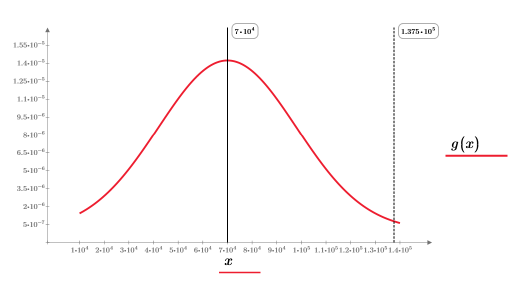
График показывает переменную T, поскольку вертикальный маркер близок к концу g (x).
Случай II: интеграл с двумя бесконечными пределами интегрирования
Задайте для переменной множителя n значение 1, а затем вычислите интеграл g(x) в диапазоне [-∞, ∞].
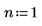
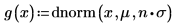
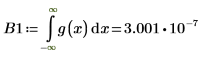
Если n=1, вычисление интеграла g(x) в диапазоне [-∞, ∞] не возвращает ошибку, а возвращает очень маленькое значение.
Обходное решение для случая II
В качестве обходного решения задайте переменным T1 и T2 значения, близкие к началу и концу g(x), а затем разделите один интеграл на три интеграла: один - для охвата диапазона [-∞, T1], второй - для охвата диапазона [T1, T2], а третий - для охвата диапазона [T2, ∞].
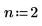
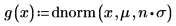
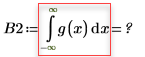
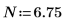 | 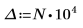 |
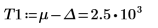 | 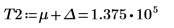 |
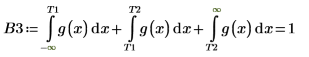
Разделенный интеграл возвращает хороший ответ при n=1 или n=2. Постройте график g(x) и добавьте вертикальные маркеры T1 и T2, чтобы увидеть, насколько они близки к началу и концу g(x).
Наблюдения и выводы
Постройте график встроенной функции плотности вероятности dnorm, используя то же самое среднее, но два различных значения стандартного отклонения.
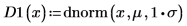
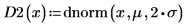
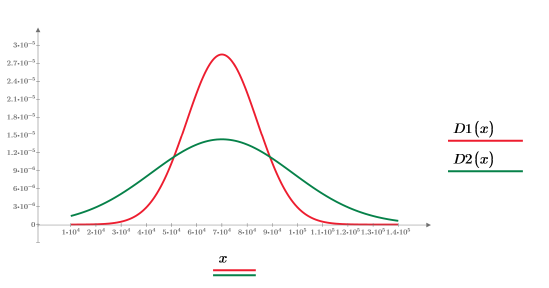
График показывает, что:
• Меньшее значение стандартного отклонения приводит к тому, что объем области под кривой будет ближе к среднему. В этом случае числовой расчет сходится, но возвращает неверный ответ.
• Большее значение стандартного отклонения приводит к тому, что объем области под кривой будет дальше от среднего. В этом случае числовой расчет не сходится.
В обоих случаях разбиение интеграла обеспечивает схождение расчета и возвращает правильный ответ.