Гипергеометрическое распределение
Следующие функции связаны с уравнением гипергеометрического распределения:
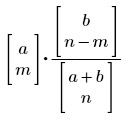
Параметры m, n, a и b — целые числа, удовлетворяющие условиям max{0, n − b} ≤ m ≤ min{n, a}, и 0 для m во всех других случаях.
• dhypergeom(m, a, b, n) — возвращает плотность вероятности для гипергеометрического распределения.
• phypergeom(m, a, b, n) — возвращает кумулятивное распределение вероятности.
• qhypergeom(p, a, b, n) — возвращает обратное кумулятивное распределение вероятности для вероятности p.
• rhypergeom(m, a, b, n) — возвращает вектор из m случайных чисел, имеющих гипергеометрическое распределение.
Аргументы
• m, n, a, b являются целыми числами, где 0 ≤ m ≤ a, 0 ≤ n − m ≤ b, 0 ≤ n ≤ a + b. Чтобы сделать возможным интегрирование и другие операции над этими аргументами, разрешены значения за пределами заявленного диапазона, но эти значения дают нулевой результат.
• p — вещественная вероятность, 0 ≤ p ≤ 1.